卷积在信号处理中的应用

文/谢沛凝

1 前言

卷积方法是“信号与系统”在论述系统对输入信号的响应而提出的，原理是将信号分解为冲击信号之和，借助系统的冲击响应，求解系统对任意激励信号的零状态响应。在“信号与系统”中，卷积是对线性时不变系统的连续时间信号即模拟信号的论述，公式表示为r(t)=e(t)*h(t)=∫ e(τ)h(t-τ)dτ 。

2 离散时间内的卷积应用

离散序列的卷积公式：y(n)=x(n)*h(n)= Σx(m)h(n-m)，此处m为负无穷到正无穷。

卷积的过程就是相当于把信号分解为无穷多的冲击信号，然后进行冲击响应的叠加，关键在于叠加。

拿生活中最简单的例子，吃饺子为列:

假设小明非常的饿，到饭店去吃饺子，每十分钟上十个饺子，一共要了一百个饺子，分十次吃完。那么在第一个十分钟内小明吃到了十个饺子，感到饱腹感。等了一会又吃了十个饺子，又有饱腹感。直到小明吃完最后十个饺子，他感觉自己跟没吃一样，为什么会产生这样的结果？

人即为系统，吃饺子即为脉冲以后，会有什么表现(输出)?

小明在很饿的情况下一次吃10个饺子相当于输出为0；如果一次连续吃20个饺子则视为输出1；吃30个饺子，他会感觉到明显的饱腹感，即输出3；一次吃40个饺子，小明可能就会很撑，相当于系统输出5；一下子吃100个饺子，他可能就输出0。

见图1，下面我用一个图表帮助大家理解，以吃饺子的个数作为X轴，以饱腹感的程度（输出）为Y轴，绘制了一条曲线：

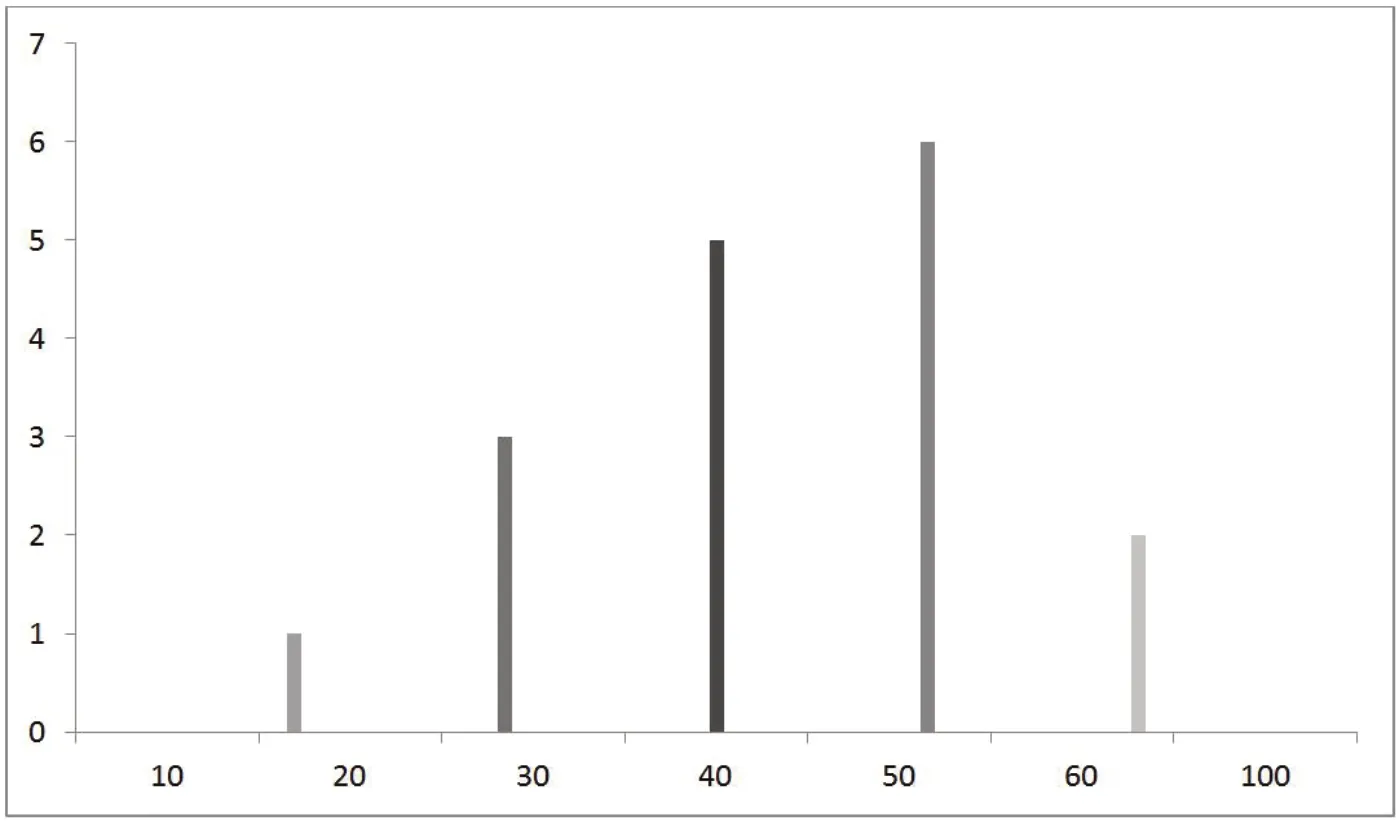
图1

小明吃100个饺子还是感到饥饿，是因为每次吃饺子的时间间隔（Δτ=1小时）太长了，所以在十分钟内，小明把吃到的10个饺子完全消化了，并没有产生叠加效应，始终是一个常数；如果缩短吃饺子的的时间间隔（Δτ=5分钟），那他的饱腹感可就迅速叠加了；等到小明吃完100个饺子时，饱腹感就会达到最大，会收到最好的效果。

这与线性时不变系统对脉冲、输入、激励的响应有关。小明吃饺子后会慢慢消化饺子，饱腹的感觉会在慢慢消失，但是不可能突然消失。这样一来，只要吃饺子的时间间隔很小，每一个饺子产生的效应都不会完全衰减，只是对最终的饱腹程度有不同的贡献。就像系统突然受到一个脉冲信号（信号瞬间消失），系统则会在某一时刻开始缓慢的衰减，直到为0。在衰减过程中又受到了一个瞬间脉冲信号，则信号会在原来衰减的地方累加上本次脉冲信号。若上次脉冲信号完全衰减为0时，本次脉冲信号则重复上次的动作，即上次脉冲对系统没有产生影响。

即：n个饺子造成的饱腹感=Σ(第m个饺子给予的饱腹感*衰减系数)，数学表达为:y(n)=Σx(m)h(n-m)。

通俗地说卷积的物理意义就在于单位冲激响应在输入信号上的叠加，对于线性时不变系统，只要知道该系统的单位冲激响应，那么求卷积就相当于把输入信号的各时间间隔的响应乘以冲激响应后相叠加，就可以直接得到输出信号。

通俗的说：在输入信号的每个位置，叠加一个单位响应，就得到了输出信号。