考虑紊流和滑移影响的液态金属润滑螺旋槽轴承设计
2019-08-22李亚倩杨攀陈渭
李亚倩,杨攀,陈渭
(西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
CT球管是CT设备的核心部件,在医学诊断、工农业及工程检测等方面有着重要的作用。由于CT球管是一件易耗品,一台CT设备一般一年需更换一至两只球管,而目前我国市场上90%以上CT产品都被GE、Philips、Siemens、Toshiba等国外品牌垄断[1-2],且价格昂贵,所以对CT球管的研究显得刻不容缓。本研究以国产化高热容量CT球管的需求为背景,针对高温环境下球管阳极靶高速旋转支承轴承——液态金属轴承的润滑机理展开研究,解决液体金属轴承长期稳定工作的关键基础问题,对国产化高性能CT设备的液态金属轴承设计具有一定的指导意义。
近年来,人们对低熔点金属的研究越来越多,其应用也越来越广泛,镓基液态金属不仅有低蒸汽压、高热导率、良好的流动性等优点,而且无毒、热物理性质稳定,将其用作滑动轴承润滑剂也是一个新的方向[3]。Hughes研究了液态金属作为高温导电润滑流体在核动力磁流体动压轴承上的应用,承载力大幅提高[4];Burton等发现高电流密度电刷经液态镓铟锡润滑后,电阻变小、发热量变低,并且具有优异的摩擦学性能[5];Cerkema则发现深沟球轴承在无氧环境下可用镓基金属作为可靠的润滑剂,其表面张力及黏合力对润滑性能影响显著[6];Kezik等研究了不同温度下液态镓的润滑性能[7];田煜研究表明极压高载条件下采用镓基液态金属润滑可有效阻止滑动界面焊合[8]。
由于螺旋槽轴承是一种具有自密封性能的轴承,无需外部供油设备,通过螺旋槽的泵压效应和周期阶梯效应形成动压油膜以实现承载,结构紧凑、稳定性好、振动噪声小、摩擦功耗低、磨损小、工作寿命长,与传统用于CT球管阳极靶支承球轴承相比,可以更好地满足阳极靶高速稳定旋转的需求。本文主要是在考虑紊流和滑移因素影响后,对液态金属润滑螺旋槽轴承进行性能研究及结构设计。
1 计算模型建立及求解
动压滑动轴承由于承载高、抗振性好,加工难度相对较低,近年来在高速旋转机械中有广泛的应用。在轴承表面加工周向、横向、螺旋、人字、复合微沟槽等不同形状的沟槽,其中存储的润滑油可以有效阻止轴承表面胶合的发生,提高轴承抗失效能力,同时也改善了轴承动压效应,使其具有良好的工作性能。动压人字形螺旋槽轴承是一种新型滑动轴承,其在光滑圆轴承表面开了一圈周向排列的人字形沟槽,由于人字形泵压效应的存在使得人字形螺旋槽轴承在不同方向均可承载。人字形螺旋槽轴承结构如图1所示。

h:油膜厚度;e:偏心距;θ:偏位角;L:轴承宽度;D:轴承直径;α:螺旋夹角;Cg:沟槽深度;Lr:凸脊宽度;Lg:沟槽宽度图1 人字形螺旋槽轴承结构示意图
1.1 螺旋槽轴承雷诺方程建立
基本雷诺方程如下
(1)
式中:Gx、Gz为紊流因子;μ为润滑介质黏度;p为油膜压力;U为轴颈线速度;x为周向坐标;z为轴向坐标。
测量润滑油黏度可知,镓基液态金属具有高温黏度稳定性,在高温时黏度基本保持恒定,因此黏度μ取常数。将U=rω和x=rφ代入式(1),并将式(1)无量纲化可得
(2)
式中:φ为无量纲周向坐标,φ=φ-θ;λ为无量纲轴向坐标,λ=z/(L/2);H为无量纲膜厚,H=h/c;P为无量纲压力,P=p/p0,p0=2ωr2μ/c2;ω为旋转角速度;r为轴承半径;c为半径间隙;Kx、Kz为无量纲紊流因子;Kx=12Gx,Kz=12Gz,ε′、εθ′分别为无量纲径向和周向扰动。
由螺旋槽轴承结构示意图可知,螺旋槽轴承沟槽走向是倾斜直线,结构特殊,直角坐标下的矩形网格会使得计算边界误差过大、计算精度差,因此需要进行坐标变换,在与沟槽走向一致的斜坐标系下[9]进行计算分析。图2给出了坐标变换示意图。
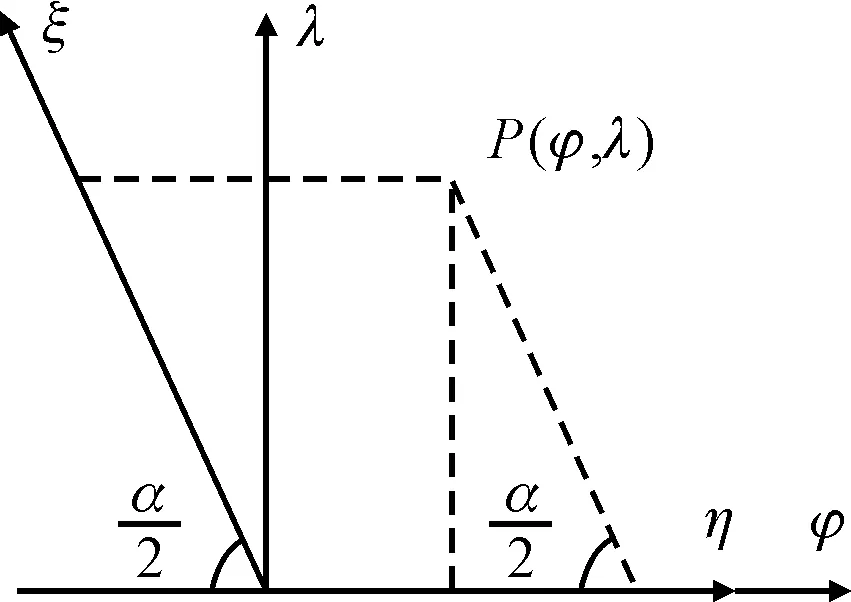
图2 坐标变换示意图
如图2所示,将直角坐标系λ-φ转换到倾斜角为α/2的斜坐标系ξ-η下,对应计算关系为
(3)
可以得到雷诺方程中压力偏导的表达式
(4)
1.2 紊流模型选取
由参考文献[10]可知,镓基液态金属黏度非常小,在室温时约为水黏度的两倍,且本研究为高速流动,因此流动形式为紊流。
常见紊流模型有壁面定律Ng-Pan模型、紊流能量方程模型、混合长度模型、整体流动模型[11]。其中,整体流动模型基本采用经验公式;紊流能量模型和混合长度模型与Ng-Pan模型计算结果基本一致,但计算过程更为复杂;Ng-Pan模型为应用最广的紊流模型,将流动形式作为接近剪切流的流动,紊流因子为线性形式,计算简便,适用于轻载动压滑动轴承,因此选用Ng-Pan模型进行计算,紊流因子Gx、Gz表达式为
(5)
1.3 滑移模型选取
一些研究表明,表面润湿性与边界滑移的发生有重要关系,产生边界滑移是固体表面液体分子克服固液表面作用力的结果,而润湿性差则代表固液界面之间作用力弱[12]。由于镓基液态金属在常用轴承材料上的接触角较大、润湿性差,因此液态金属润滑时需要考虑边界滑移问题。
边界滑移是指固体表面液体分子同固体表面间存在相对切向运动速度。传统用于处理边界滑移问题的物理模型有滑移长度模型(SLM)和极限剪应力模型(LSSM)两种,表达式分别为
(6)
滑移长度模型为线性关系,滑移长度恒定,求解简便,但是很多实验结果表明,滑移长度是随着固液界面之间剪应力变化的,剪应力越大,滑移长度越长,因此滑移长度模型不够准确;而极限剪应力模型认为固液界面之间存在极限剪应力决定滑移是否发生,在高剪切率时的计算比滑移长度模型准确,但数值计算复杂,存在强非线性边界待定问题,对于二维流动,滑移可以发生在任意方向,迭代求解基本不可行。
Spikes和Granick则将两种模型结合,当固液界面间剪应力大于极限剪应力时,才会发生边界滑移,且滑移长度遵从线性滑移长度模型[13]。该方法解决了二维流动数值分析困难的问题,同时将极限剪应力因素考虑进去,使得计算结果也更准确,表达式如下
(7)
式中:τco为极限剪应力;b为滑移长度;us为滑移速度。考虑滑移影响后的雷诺方程表达式为
(8)
将剪应力代入式(8)可得滑移速度的表达式为
ux=
(9)
z方向与x方向类似。将上述雷诺方程转化为无量纲形式
(10)
式中:Ux=ux/U;Uz=uz/U。
1.4 方程求解
由于斜坐标下方程离散计算比较复杂,下面以层流无滑移静态雷诺方程为例说明离散过程的处理。
一般直角坐标下的计算是直接对雷诺方程中的偏导进行差分处理,而在斜坐标下计算得到的方程存在交叉偏导项,直接差分会有非节点处的压力值存在,不能采用五点差分法,对此采用局部积分法进行处理。
对螺旋槽轴承沿人字形走向及其边界划分m×m网格,局部积分法具体过程如下。
对雷诺方程两边分别在如图3所示平行四边形区域进行面积分
(11)
转化为线积分
(12)
将坐标转换和压力偏导表达式代入整理,得到斜坐标下的五点差分公式
Pi,j=
(13)
式中
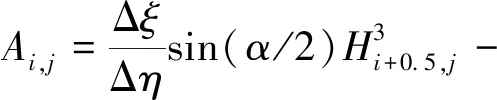
(14)
人字形沟槽的存在使得周向网格划分存在膜厚不连续处,即节点落在凸脊和沟槽的交界处,膜厚存在阶梯变化,对此只要分别对图3左右两部分分别进行局部积分即可。对于动态雷诺方程,直接用小扰动法进行处理,离散形式与静态方程类似。

图3 螺旋槽轴承网格划分及局部积分示意图
由于人字形螺旋槽轴承结构的对称性,选取z方向上的一半进行研究即可,如图4所示。
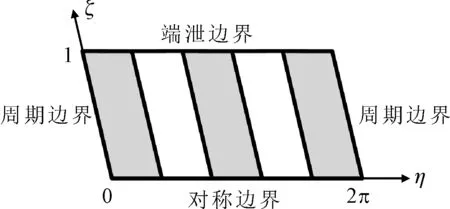
图4 人字形螺旋槽轴承边界示意图
螺旋槽轴承静态雷诺方程边界条件如下
(15)
对于对称边界的计算,只需对压力对称赋值即可。螺旋槽轴承动态雷诺方程边界条件则是在由上面静态雷诺边界确定的完整油膜区域的周边,扰动压力取0。图5给出了螺旋槽轴承性能计算总流程图。
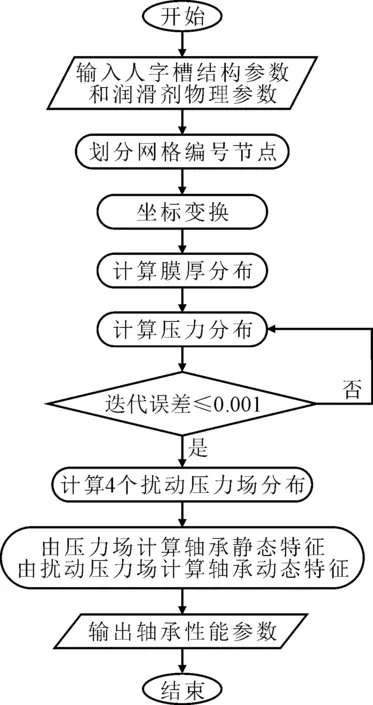
图5 螺旋槽轴承性能计算总流程图
对于滑移部分的迭代,第一轮迭代时Ux、Uz取0,计算得到P分布,而滑移仅可能发生在当滑移速度不等于0的情况下。如发生,判断滑移速度方向,并计算得到滑移速度,代入上述雷诺方程,重新迭代求解P,直至满足收敛精度。x方向判断式如下
(16)
z方向的判断与x方向类似。
归一化承载力表达式为
(17)
泄流量
(18)
摩擦阻力
(19)
摩擦功耗
Nt=FtU
(20)
平均温升
(21)
归一化刚度
(22)
归一化阻尼
(23)
归一化相当刚度
(24)
归一化临界涡动比平方
(25)
归一化临界质量
(26)
1.5 模型验证
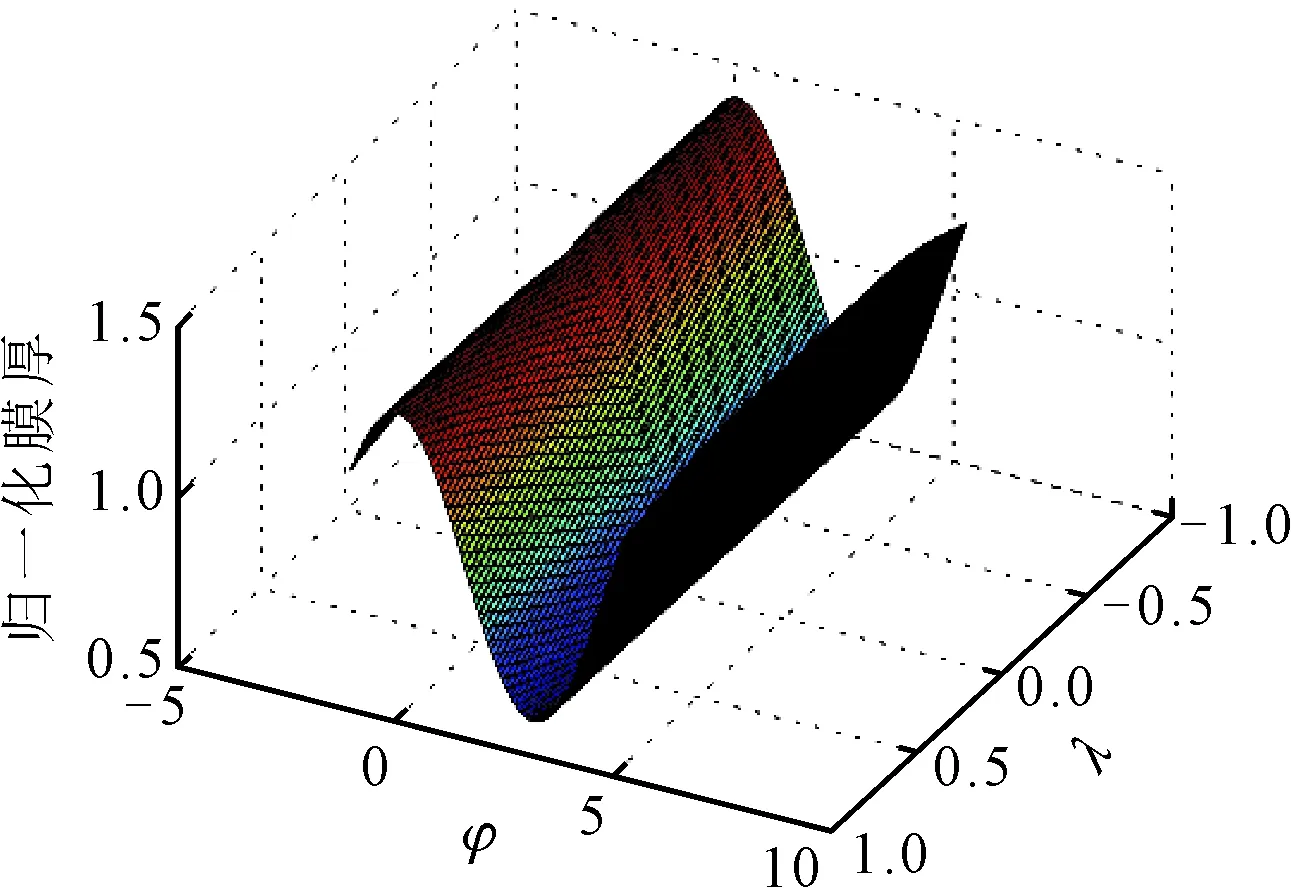
图6给出了斜坐标下推导的螺旋槽轴承计算模型得到的光滑圆轴承表面的膜厚压力分布图。
如图6所示,由推导得到的斜坐标下的压力迭代系数求解得到光滑面圆轴承在偏心为0.4时的膜厚及压力分布,在膜厚最小处附近压力达到峰值点,压力峰值点在周向坐标145°附近。计算得到了斜坐标下圆轴承不同偏心下的承载力,并与文献[11]中对瓦张角为2×180°、宽径比L/D为1的圆轴承无量纲承载力进行了对比,如图7所示。
(a)圆轴承膜厚分布

(b)圆轴承压力分布图图6 斜坐标下光滑圆轴承表面的膜厚压力分布
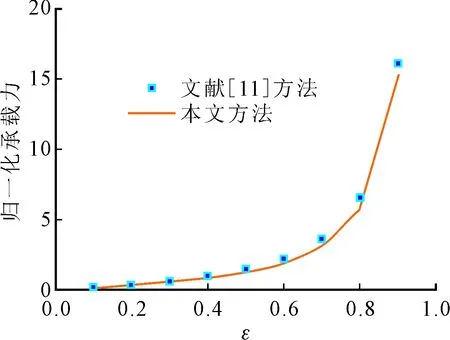
图7 斜坐标不同偏心率下圆轴承承载力的对比
由图7可知,采用斜坐标下轴承计算模型计算得到的不同偏心率下的圆轴承承载力与文献[11]保持了高度的一致,误差在10%以内,验证了计算模型的正确性。
2 结果分析与讨论
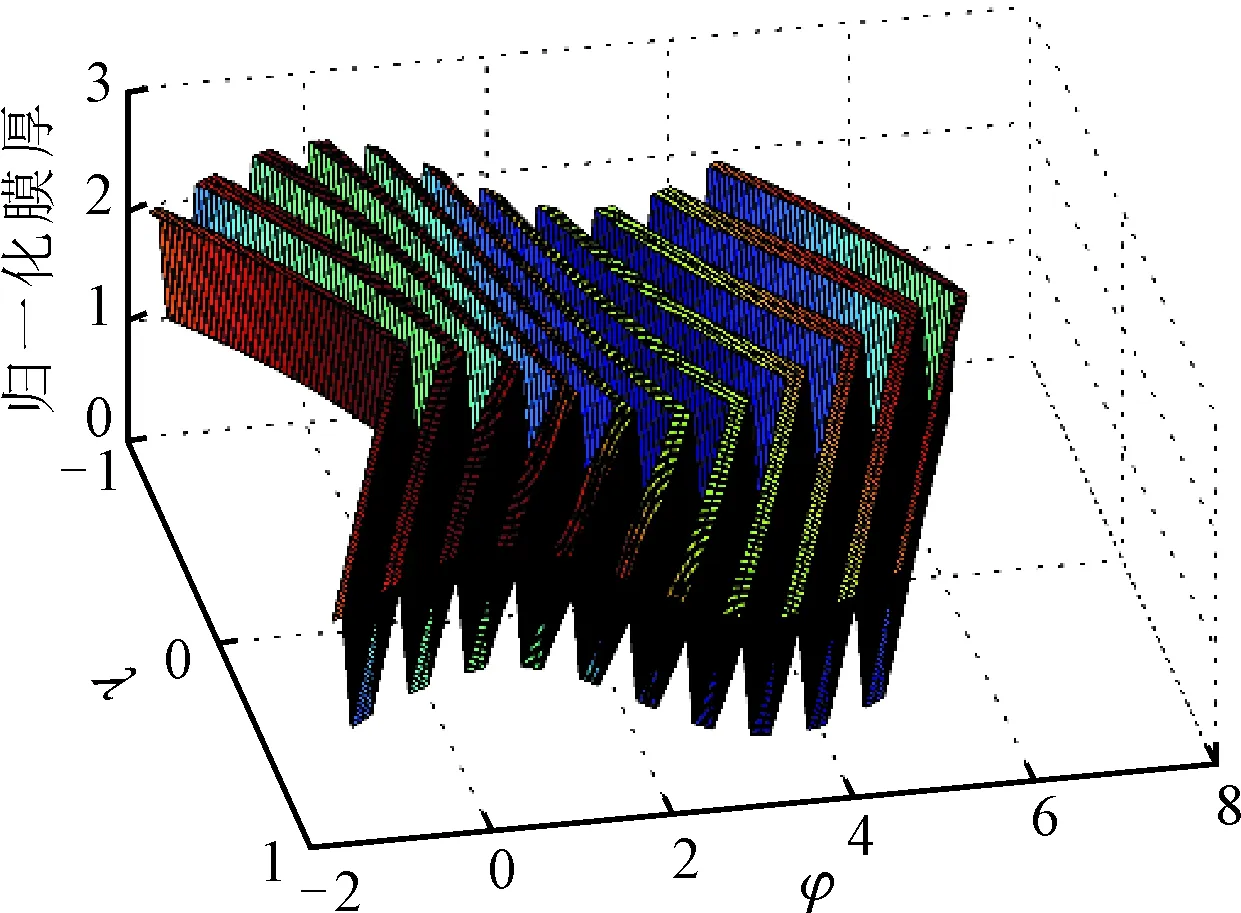
以下分析采用螺旋槽轴承及润滑剂参数:轴承直径为30 mm,宽径比L/D为1,半径间隙为0.02 mm,槽数为10,槽深为0.02 mm,螺旋角为60°,沟脊比Lg/Lr为1,轴承轴颈转速为10 800 r/min;镓铟锡合金密度为6.44 g/cm3,黏度为0.001 8 Pa·s,比热容为365.6 J/(kg· ℃)。图8给出了计算得到的螺旋槽轴承膜厚压力分布图。
(a)膜厚分布

(b)压力分布图图8 螺旋槽轴承膜厚压力分布
如图8所示,在膜厚最小处附近压力值达到最大,且由于楔形效应和人字沟槽泵压效应同时存在,因此压力不只存在一个峰值点。通过比较小偏心率和大偏心率时的压力分布图可知,在小偏心率时压力沿周向走势平缓,大偏心率时压力峰值突出,变化剧烈。在小偏心率情况下轴承以人字槽的泵压效应提供压力为主,压力比较分散,主要分布在沟槽处且峰值较小,而凸脊处几乎无压力分布;在大偏心率情况下轴承整体楔形效应更加明显,压力分布较集中,峰值较大,峰值点减少,并且主要分布在凸脊处。
2.1 螺旋槽轴承静动态性能分析
图9给出了在层流无滑移情况下的螺旋槽轴承静动态性能参数随偏心率的变化。
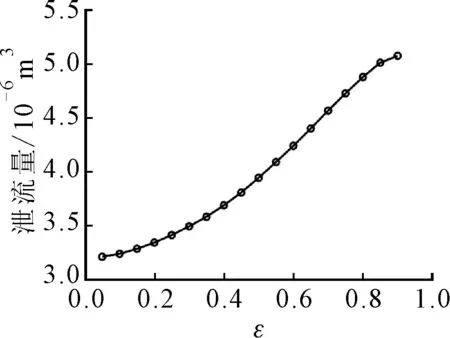
(a)承载力(b)泄流量
随着偏心率的增大,轴承与轴瓦之间间隙减小,楔形效应增加,油膜压力增大,承载力增加。同时,泄流量随偏心率的增加基本呈线性增长。间隙减小,摩擦阻力先缓慢增大,随着偏心率增加到0.6左右时,油膜越来越薄,剪切力显著增加,摩擦功耗迅速升高。因此,受摩擦功耗与泄流量影响,温升先小幅降低后,在偏心率增加到0.6时,温升迅速升高,总体温升都在15 ℃以内。同时,随着偏心率的增大,刚度和阻尼基本都保持增加。
2.2 紊流与滑移对轴承性能的影响
2.2.1 紊流效应的影响 在采用Ng-Pan紊流模型后,紊流与层流下的轴承性能的对比如图10所示。
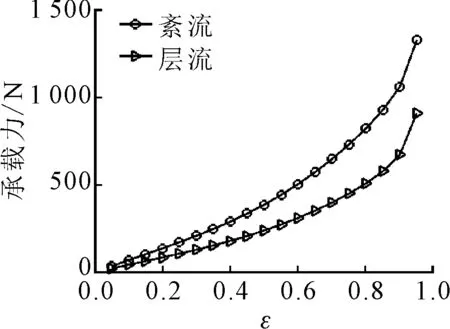
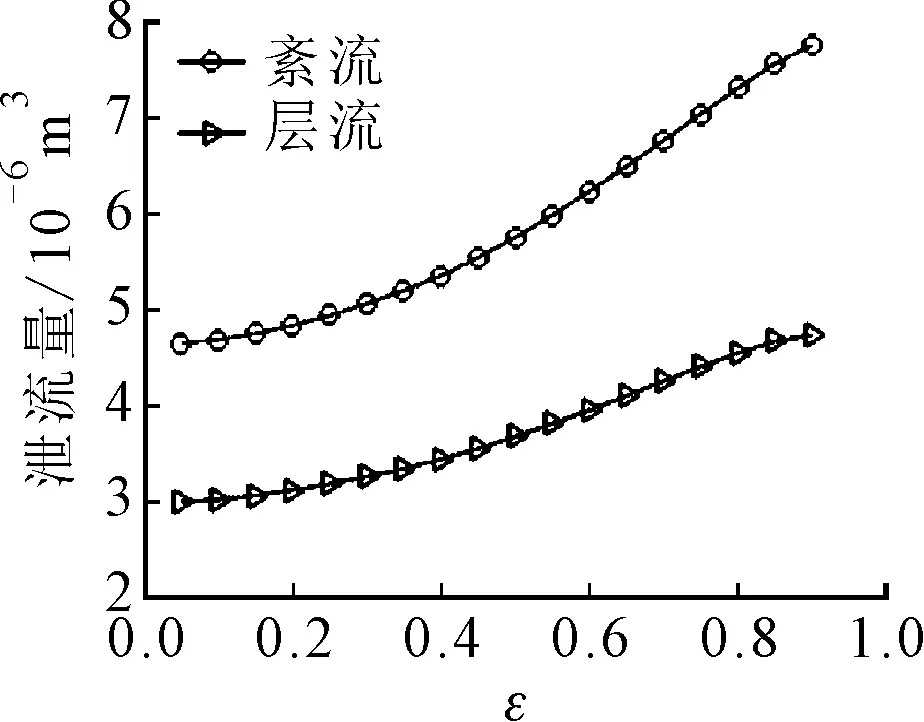
(a)承载力(b)泄流量

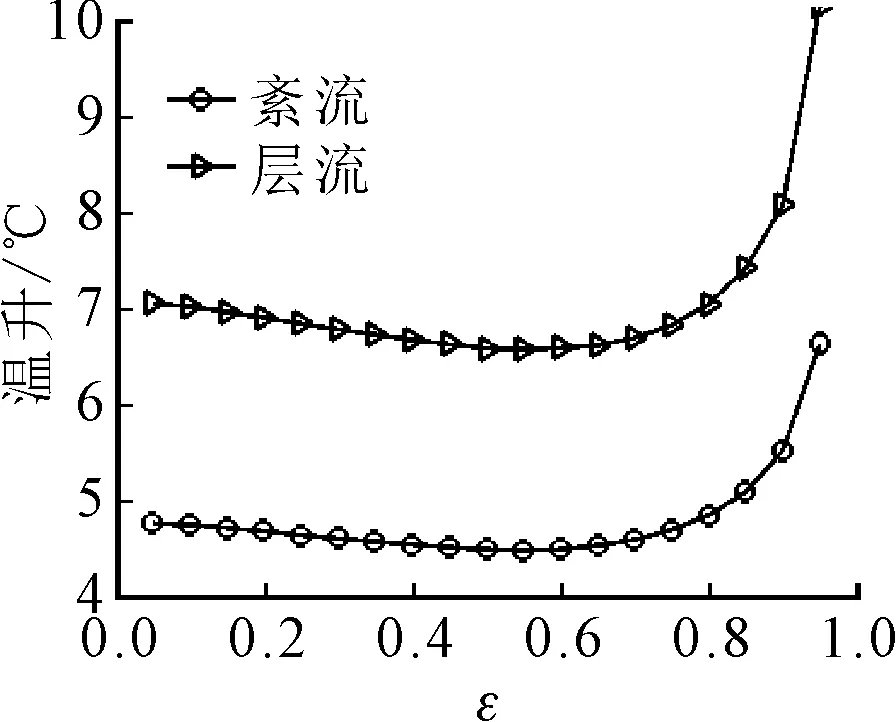
(c)摩擦功耗(d)温升
可以发现,考虑紊流效应后,轴承承载增加,由于流体分子运动剧烈,泄流量增大近一倍,同时,归一化摩擦功耗有所增加,但增加幅度较泄流量增加小,因此,轴承整体温升是降低的。由此可见,液态金属润滑螺旋槽轴承在考虑紊流效应后轴承整体性能有所提升,是有利的。
2.2.2 边界滑移的影响 图11给出了光滑圆轴承发生边界滑移后的周向压力对比图。A、B、C为3种具有不同滑移范围角的圆轴承。A表示普通轴承,B表示滑移和非滑移表面各占一半,轴承C表示整个表面均发生滑移。
由图11可知,与普通轴承相比,发生全滑移的轴承C空化区域基本不变,整体压力分布以及承载能力要比普通轴承小;而发生半滑移的轴承B压力分布范围要比普通轴承更大,空化区域明显减小。
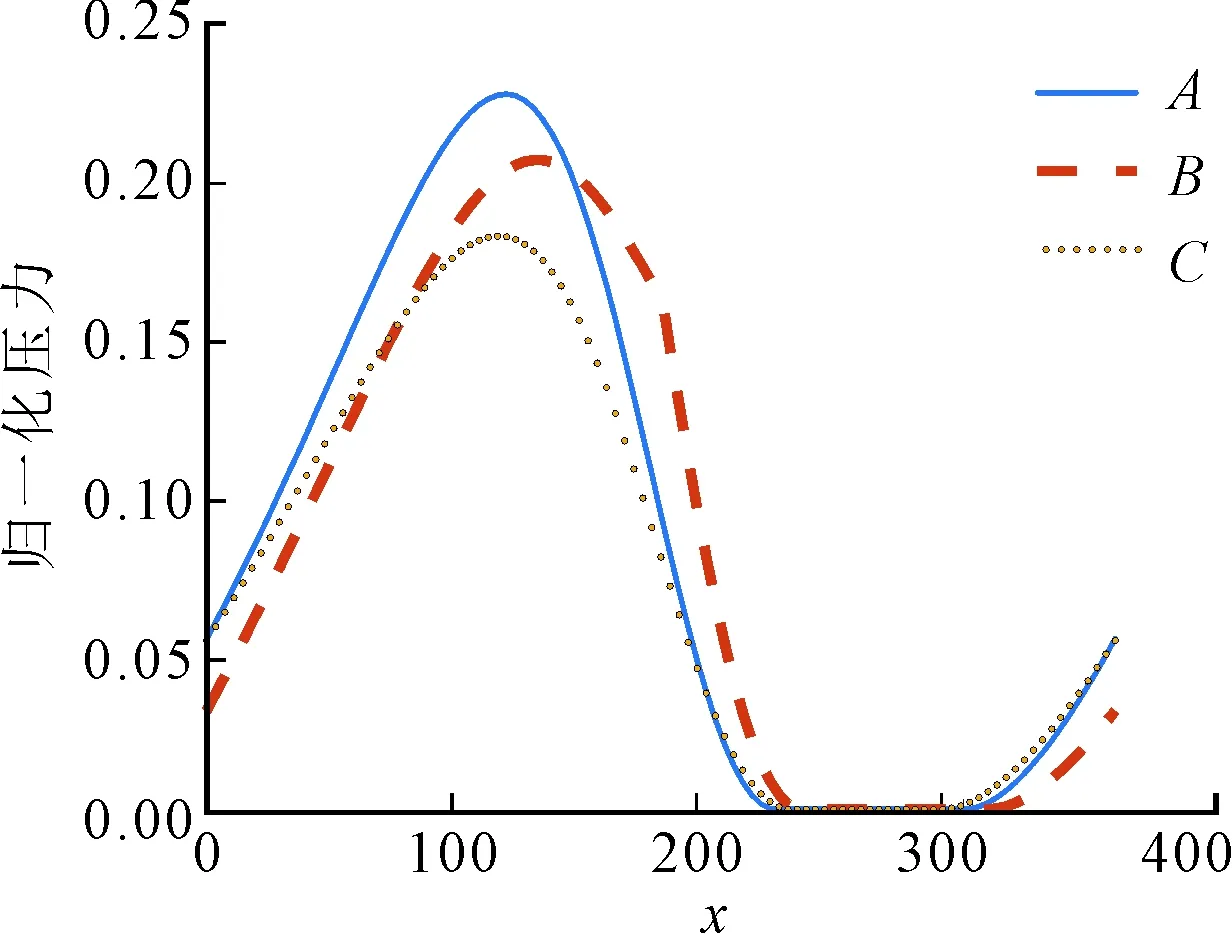
图11 光滑圆轴承发生边界滑移后的周向压力对比
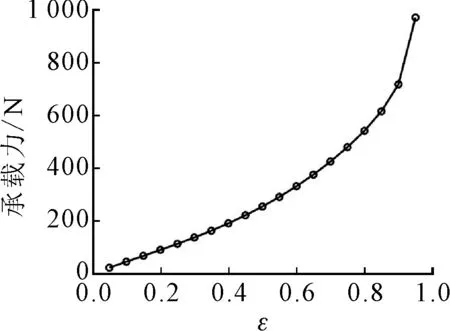
图12给出了采用全滑移、半滑移、无滑移表面计算得到的螺旋槽轴承滑移与无滑移的承载能力对比,可以发现,全滑移使得轴承承载能力降低,而半滑移轴承承载能力要大于无滑移表面。可以考虑对轴承材料进行表面处理来避免滑移现象发生,或者是达到半滑移效果,减少空化区,提高承载能力。
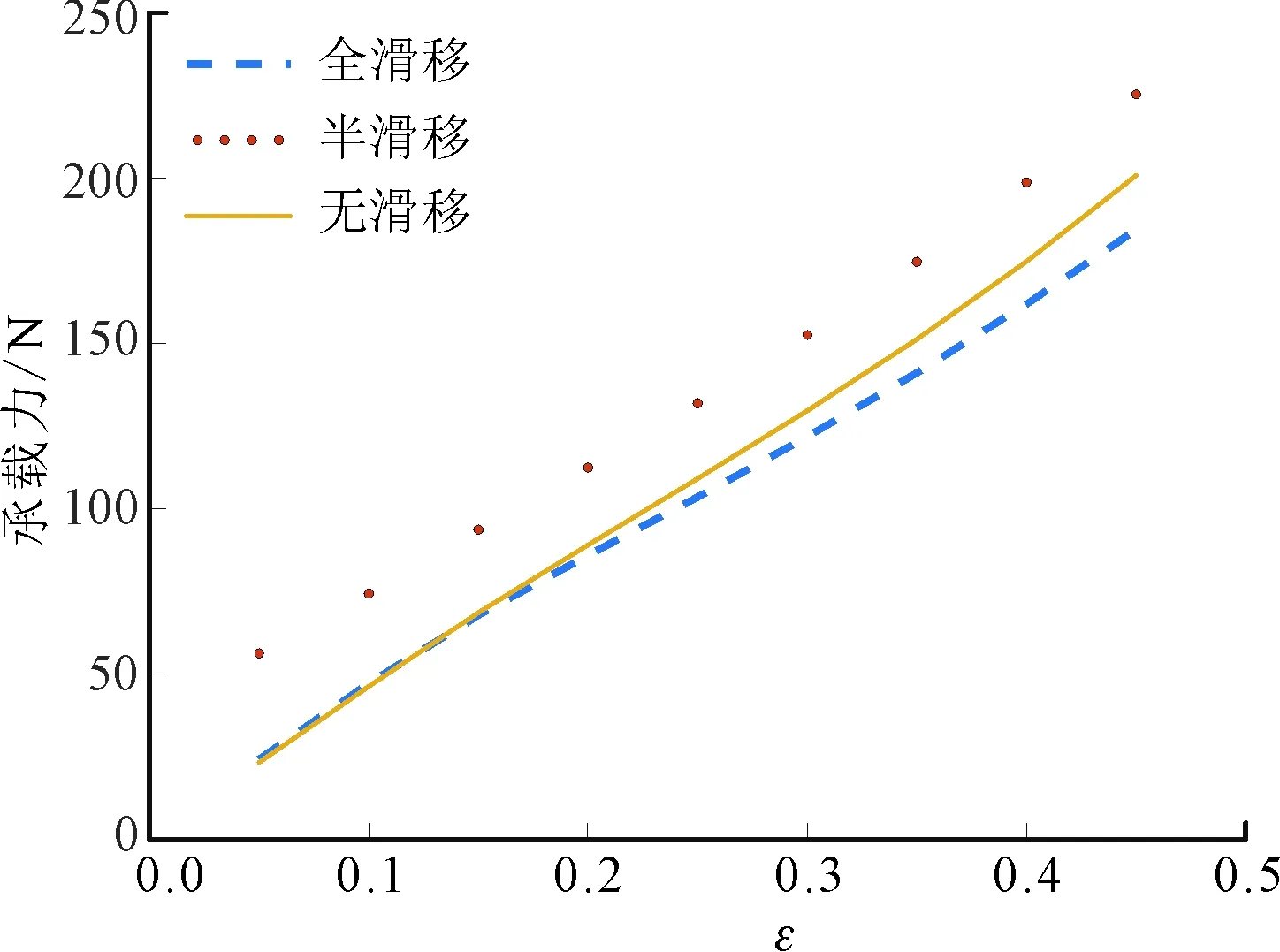
图12 滑移对轴承承载力的影响
2.3 螺旋槽轴承结构设计
本节分析螺旋槽轴承槽数、夹角、槽深、沟脊比等结构参数对轴承性能的影响,在高承载、刚度及稳定性目标下确定轴承各结构参数的具体取值范围。
保持其他参数不变,偏心率固定为0.4,改变槽数,取槽数为5、8、10、12、15、20、25和30,分析槽数对螺旋槽轴承承载力以及相当刚度的影响。如图13所示,承载力随槽数的增加先迅速增大,槽数增加到24时达到最大值,然后缓慢减小,但整体变化幅度不大;归一化相当刚度系数随槽数的增加先升高然后快速降低,可见轴承槽数过多对轴承刚度不利,槽数为8时刚度最大。
对比图13可以发现,槽数对轴承相当刚度的影响较对承载力的影响大,因此,综合考虑承载力和刚度,槽数取8~12个即可。
保持其他参数不变,槽数取10,改变螺旋夹角从30°到180°,分析螺旋槽轴承承载力以及临界质量随槽数的变化。
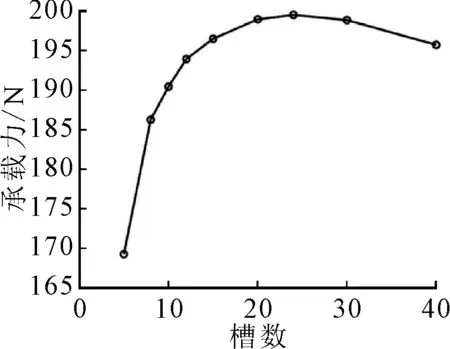
(a)承载力
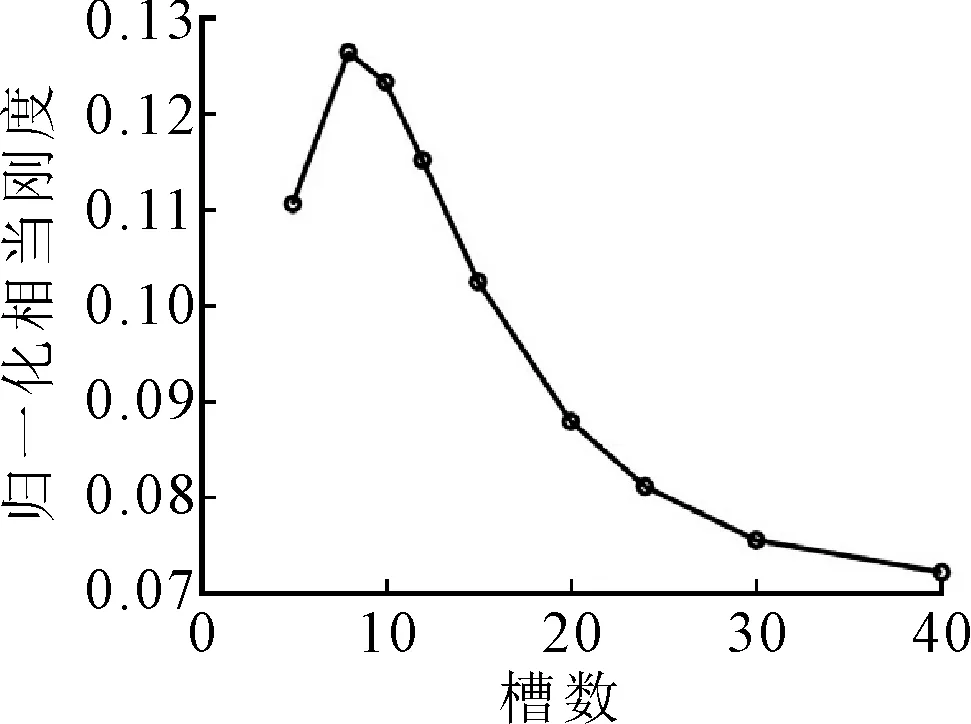
(b)相当刚度图13 槽数对轴承性能的影响
如图14所示,随着螺旋夹角增大,承载力先增大后减小,在60°左右达到最大值,说明轴承在螺旋夹角为60°时泵压效应达到最佳,且夹角对轴承承载力影响比较大。在直沟槽,即夹角为180°时,承载力在同等条件下比夹角为60°时要小接近一半。归一化临界质量M随螺旋夹角增大而增大,然后到60°之后基本保持稳定,说明轴承在小夹角时稳定性差,在夹角增大到60°后稳定性好,且螺旋夹角在60°时比30°的临界质量要高两倍多。因此,螺旋夹角一般取60°左右。
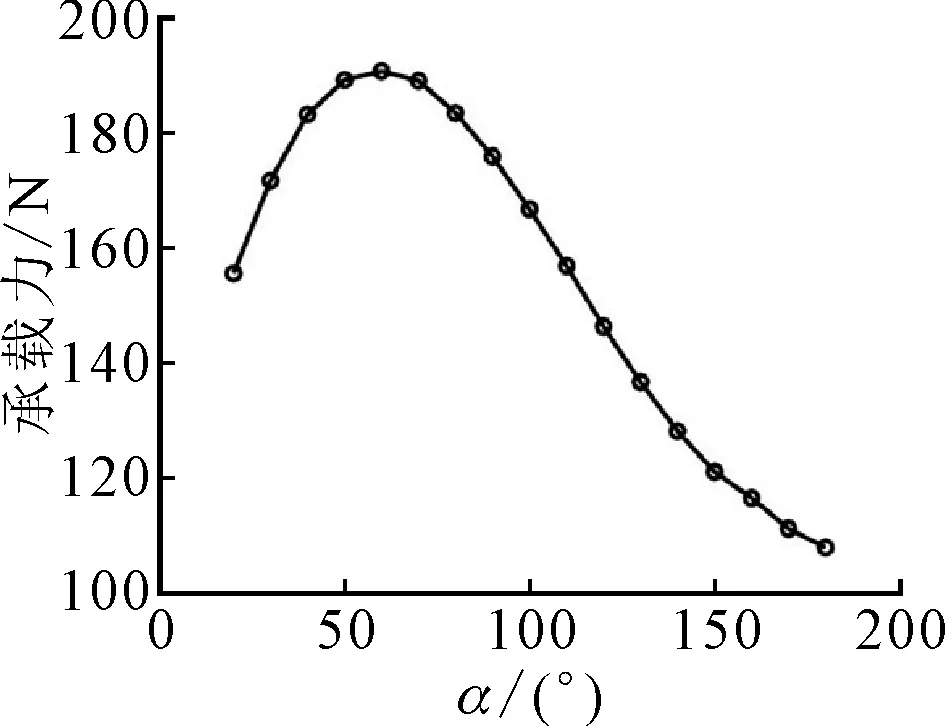
(a)承载力

(b)临界质量图14 螺旋夹角对轴承性能的影响
保持其他参数不变,改变螺旋槽槽深分别为10、15、20、30、40 μm时,分析槽深对螺旋槽轴承静动态性能的影响。如图15所示,承载力随槽深增大而减小,槽深变化量一定时,槽深越小,对承载力影响越大。摩擦功耗也是随槽深增大而减小,槽深较小时的变化对摩擦功耗影响较大。综合考虑承载和摩擦功耗,螺旋槽槽深不能太大,否则承载力差;也不能太小,否则摩擦功耗过大。因此,一般选取槽深为20 μm左右。
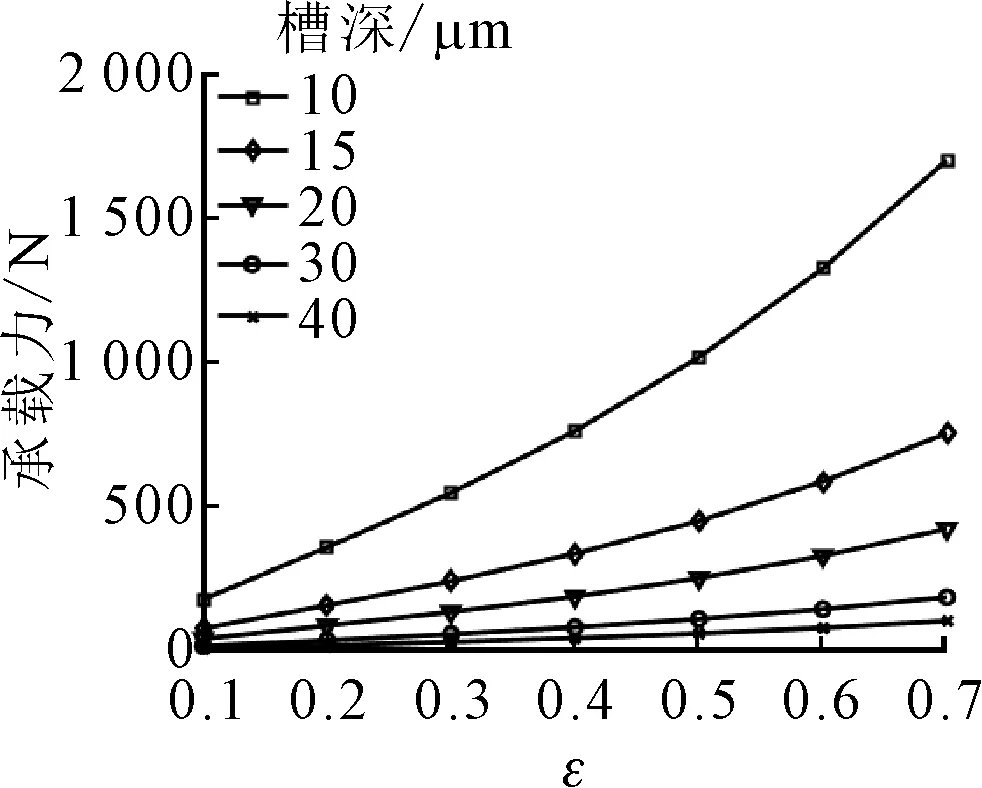
(a)承载力

(b)摩擦功耗图15 槽深对轴承性能的影响
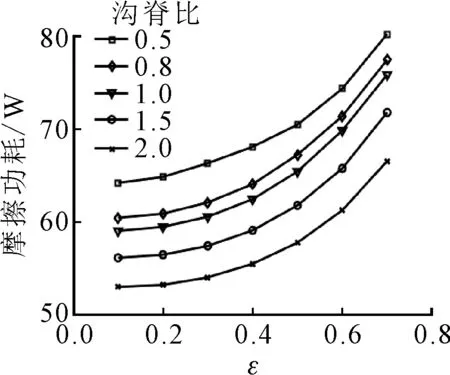
(b)摩擦功耗图16 沟脊比对轴承性能的影响
保持其他参数不变,改变螺旋槽沟脊比分别为0.5、0.8、1.0、1.5、2.0时,分析沟脊比对螺旋槽轴承静动态性能的影响。如图16所示,随着沟脊比的增大,承载力减小,则沟脊比不宜过大。摩擦功耗基本成比例减小,沟脊比每增加0.5,摩擦功耗降低10%。沟脊比过大,则承载低;沟脊比过小,则摩擦功耗大。因此,一般选取沟脊比为1,即沟宽与脊宽相等时,可以达到承载力与摩擦功耗的平衡。
3 结 论
本文考虑紊流和边界滑移的影响,分析了镓基液态金属润滑螺旋槽轴承的承载力、泄流量、摩擦阻力、温升、刚度以及阻尼随偏心率的变化情况。采用Ng-Pan紊流模型以及综合滑移长度模型(SLM)和极限剪应力模型(LSSM),分析对比了考虑紊流滑移影响和层流无滑移时的轴承性能;分别研究了螺旋槽轴承槽数、螺旋夹角、槽深、沟脊比等结构参数对轴承静动态性能的影响,得出了以下结论。
(1)螺旋槽轴承由泵压效应和楔形效应共同提供承载,在小偏心率情况下以人字形槽的泵压效应提供压力为主,在大偏心率情况下轴承整体楔形效应更加明显。
(2)考虑紊流影响后轴承承载能力增加,同时,全滑移效应的存在使得螺旋槽整体承载能力降低,而适当的半滑移效应则有效提高了轴承承载能力,减少了空化区,因此可以考虑进行表面处理使得滑移对轴承性能产生有利的影响。
(3)综合考虑承载、刚度等因素,螺旋槽轴承在槽数取8~12、螺旋夹角取60°左右、槽深取20 μm左右、沟脊比取1时,可以获得比较良好的静动态性能。
