气体轴承的动态特性分析及实验研究
2019-08-22任佟陈东菊李彦生范晋伟
任佟,陈东菊,李彦生,范晋伟
(北京工业大学先进制造技术北京市重点实验室,100024,北京)
气体轴承作为主轴系统中支撑主轴回转运动的重要元素,其性能将直接影响主轴在工作中的运动精度,并对加工零件的表面质量、形状精度及粗糙度造成重要影响[1]。气体轴承的动态特性在很大程度上决定系统的动态特性。轴承的动态特性是通过轴承的阻尼系数和动态刚度来衡量的。气体轴承工作时,微小气膜间隙产生气膜波动,气膜阻尼会抑制气膜波动,因此气膜阻尼成为影响气体轴承动态特性的重要因素。然而,空气黏度仅为液压油的1/1 000,这样导致气体的阻尼特性很差,为了更准确地分析气体轴承的动态特性,有必要对主轴的气膜阻尼进行研究。
一些学者在微机电系统下建立了气膜阻尼模型。Pandey等和Altu等通过格林公式研究了不同条件下弹性平板间的阻尼分布情况[2-3];李锡广等针对MEMS陀螺中带孔结构建立了空气阻尼计算模型[4];Xia等提出了圆形和椭圆形微扭镜的挤压薄膜空气阻尼系数[5];周浩等仿真计算了微陀螺仪表芯结构的空气阻尼系数[6];Li等、Homentcovschi等和高春晖等针对不同形状的穿孔微孔板挤提出了压膜阻尼的计算分析模型[7-9];Moeenfard等采用EKM分析了微镜中挤压薄膜阻尼问题[10];Ghanbari等提出了一种用于研究面内振荡微束谐振腔中流体薄膜阻尼的数学模型[11];陈奥运建立了敏感模态压膜阻尼简化分析模型[12];Wang等分析了平行板驱动器中的挤压膜阻尼系数对环境的影响[13]。然而,这些模型对于气浮轴承并不完全适用。
气膜波动使气体轴承不稳定,从而引起主轴系统不稳定[14],因此要基于气膜阻尼特性研究轴承的动态特性。Wardle等设计了一种快速响应、高分辨率的外部阻尼控制系统[15];Wang等模拟了关键结构参数变化的阻尼特性[16];Rudloff等将实验和理论确定的轴承动态特性系数对比分析[17];Chen等发现气膜厚度小、供气压力高的超精密气体轴承,其非线性动力学行为十分显著[18];贾晨辉等发现球面螺旋槽气体轴承在最大承载力下,随轴承偏心率的增加,刚度系数明显增大,而阻尼系数变化较缓[19];Yu等通过数值模拟和实验研究发现扰动影响气浮轴承的动态特性[20]。这些研究证明了气膜阻尼系数是动态变化的,并且会对轴承的动态特性造成影响。
本文提出了一种气体轴承的无量纲气膜阻尼系数模型,并将气膜阻尼模型引入到弹簧阻尼单元中,最后搭建气体轴承回转误差试验台,得到主轴实时回转跳动误差信号。该研究方法对预测气体轴承的动态特性以及进一步提高主轴系统的运动精度和稳定性具有现实意义。
1 气体轴承的工作原理及结构
气体轴承依靠外部气源的恒压供气,在轴承间隙中形成具有一定压力和刚度的润滑气膜,所以气膜对主轴转子起到润滑和支撑作用。图1为气体轴承的结构及工作原理图。气体轴承系统主要由气源、节流器和轴承3部分组成。环境气体进入空气压缩机后形成具有初始压力的压缩气体,气体经过干燥器、过滤器、调压阀等元件得到湿度适宜、洁净的气体,通过进气孔进入气体轴承,经由各个节流器进入轴承间隙,形成厚度为h0的润滑气膜,最终从轴承端部流入外部环境中。气体轴承采用4排节流孔分布,每排沿周向均布8个节流孔,节流孔采用小孔节流方式。气体静压主轴在工作过程中,轴承微小气膜间隙限制主轴的自由度,而轴承微小气膜间隙会发生变化,容易产生气膜波动,使主轴产生位移,从而影响主轴的回转精度。气膜阻尼是影响气膜波动的重要原因。本文研究的气体轴承相关参数如表1所示。

图1 气体轴承的结构及工作原理图

参数数值转子长度L/mm100轴承直径D/mm50轴承间隙h/μm12质量偏心距e/μm0.5转子质量m/kg26.8
2 气体轴承气膜阻尼特性分析
2.1 气膜阻尼模型
根据气体轴承气膜阻尼的产生机理,阻尼可以分为两类:第一类是滑膜阻尼,它直接作用在流体介质与转子、定子的接触面上,与转子转动方向一致,由流体的黏性作用产生,在气体轴承中,滑膜阻尼值特别小可以忽略;第二类是挤压膜阻尼,它是由于流体介质上下接触面存在一定的压差而产生,垂直于转子的转动方向。由于气源系统供气压力不稳,气膜与转子、定子的气固耦合等原因使主轴系统存在振动,这种情况下气膜存在挤压膜阻尼力。结合空气静压径向轴承的工作原理和结构,建立雷诺方程
(1)

令x=lX,z=lZ,t=t/w,得到无量纲气体阻尼方程
(2)
式中:η=Δh/h0,Δh为气膜厚度变化量;ψ=Δp/p,Δp为压强变化量;w为主轴径向频率;σ为考虑速度滑移的相对挤压数
(3)
采用微扰动法,假设气体静压主轴系统的振动符合简谐振动公式η=εcosT,ε为无量纲振幅,则式(2)变为
(4)
式(4)可采用分离变量法求解,根据二阶非齐次偏微分方程求解方法,假设解的形式为
ψ(X,Z,T)=ψ1(X,Z)sinT+ψ2(X,Z)cosT
(5)
式中:ψ1(X,Z)为气膜中产生的阻尼力;ψ2(X,Y)为气膜中产生的弹性力。
假设理想情况下,气膜内压力呈对称分布,可表示为下列方程
(6)
式中:aij、bij为傅里叶系数,通过主轴系统的运动来确定其数值,其中
(7)
则有
(8)
对式(8)进行面积分后,可得到阻尼力
(9)
因此,无量纲气膜阻尼系数cd为
(10)
式中:l为矩形气域区域边长;β为研究的气膜区域的长宽比,β=1;i、j为式(4)的本征值,i=1,j=1。
同理,可以得到刚度系数ke为
(11)
2.2 气膜阻尼特性分析
根据气体轴承试验台结构参数,令气体主轴系统的标准工况为:供气压强p=0.3 MPa;主轴转速n=100 r/min。通过MATLAB对无量纲气膜阻尼模型求解。给定供气压强和主轴转速的边界范围,控制单一变量求出每个节点的无量纲气膜阻尼系数cd,最终分别得到供气压强p、主轴转速n与无量纲气膜阻尼系数的关系,结果如图2和图3所示。

图2 供气压强和无量纲气膜阻尼系数之间的变化关系

图3 主轴转速和无量纲气膜阻尼系数之间的变化关系
从图2可看出,气体轴承的供气压强和无量纲气膜阻尼系数呈非线性关系。由变化趋势可知,供气压强小于0.4 MPa时对气膜阻尼系数有影响显著,这是因为随着供气压强的增大,每层气膜之间的相互阻尼力增加,导致阻尼系数增加;当供气压强增加到某一值时,轴承间隙的气量到达峰值,阻尼力变化不大,导致阻尼系数变化趋势变缓。从图3可看出,气体轴承的主轴转速和无量纲气膜阻尼系数呈线性关系。这是因为随着主轴转速的增加,轴承间隙的气膜流速加快,从而导致气膜阻尼力和阻尼系数增加。这说明主轴系统不同的工况对阻尼系数有不同的影响,所以有必要对气膜阻尼特性进行研究,进而探究气膜阻尼对气体轴承动态特性的影响规律。
3 气体静压主轴动态特性分析
3.1 气体静压主轴振动误差表征
主轴的振动误差主要包括跳动误差和偏摆误差,而跳动误差又包括X方向的跳动误差和Y方向的跳动误差,如图4所示。在X方向上,转子偏心旋转时,偏心质量的自激振动产生偏心振动位移x;外力Fr=0.015 N使转子产生偏摆角度θ,其受迫振动也会产生偏心振动位移x′,这两部分位移组成了X方向上的跳动误差Δx。同时,在Y方向上的偏心旋转也会产生偏心振动位移y,即Y方向上的跳动误差Δy。结合图4可知,空气静压主轴的振动误差公式为
(12)
式中:ΔE为主轴径向总误差。

图4 气浮主轴径向振动误差分析
3.2 气体静压主轴动力学分析
为了研究气膜的波动对气体主轴动态特性的影响,根据气体轴承的结构,将气膜简化为X方向和Y方向两个相互垂直的弹簧阻尼系统,建立轴承和转子的动力学模型。转子质量为m,转子质心点O,O′为某一时刻质心的振动位置,将X方向和Y方向的弹簧阻尼系统分别编号为1~8。如图5所示。
假设在某一时刻,主轴X方向和Y方向的振动位移分别为Δx和Δy,结合模型对转子受力分析,如图6所示。Fx和Fy是转子旋转过程中偏心力在X方向和Y方向上的分力,Fi(i=1,2,…,8)是对应编号的弹簧阻尼力,xi(i=1,2,…,8)是各弹簧阻尼力作用点的振动位移。进行受力分析可得轴承-转子系统的振动方程为
(13)
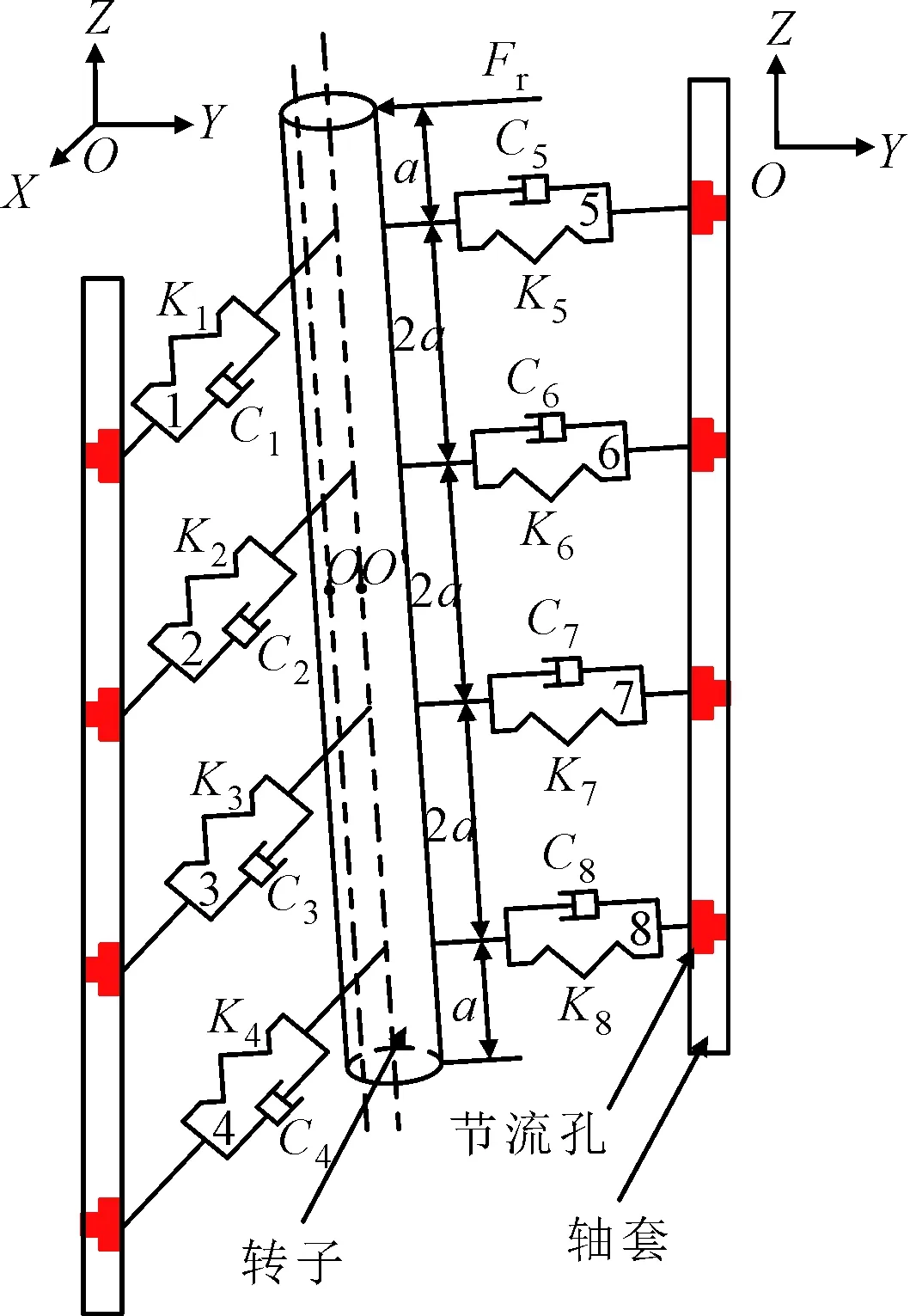
式中:Ki为编号为i的弹簧阻尼系统的刚度系数;Ci为编号为i的弹簧阻尼系统的阻尼系数;e为主轴偏心距;W为转子旋转的角速度。根据受力分析及位移分析,以质心O为原点,建立各弹簧阻尼力作用点的位移xi如下
(14)
式中:a为主轴转子长度的1/8。将式(14)代入式(13),整理得转子-轴承系统的动力学振动矩阵模型为

(15)
式中
(16)
4 仿真结果分析及实验研究
4.1 振动结果分析

图7 采用MATLAB求解转子轴承系统振动流程图
根据转子的结构参数,再输入影响轴承动态特性的转子工况供气压强和主轴转速,通过MATLAB求解模型获得轴承-转子系统在时域上的振动特性,分析主轴的振动规律,MATLAB运算流程如图7所示。通过改变单一工况得到轴承-转子系统在时域上不同的振动特性,分析阻尼对主轴振动的影响。图8~图10是气体静压主轴振动特性曲线,通过分析与对比可以得到以下结论。
(1)从图8可以看出:主轴系统的回转跳动误差信号在以一定频率的振动过程中同时作一定幅值的上下振动,这是由主轴转子偏心运动和外载荷Fr造成的;同时,跳动振幅大部分偏向y轴正方向,表明径向力增加了加载方向上的振动;转子开始转动时,转子的振幅从零迅速上升至某一值,出现较大幅值的跳动,这表明主轴系统启动时转子不稳定的振动特性;最终在振动过程中趋于稳定,这说明气膜的阻尼特性对转子振动起到了抑制作用。

图8 转子跳动误差曲线
(2)从图9可以看出:随着供气压强的增加,转子跳动误差减小;供气压强从0.3 MPa增加到0.5 MPa时的跳动误差减小值比供气压强从0.5 MPa增加到1 MPa时的跳动误差减小值大;当气膜阻尼系数明显增加时,转子的跳动误差明显减小,转动更加稳定;当气膜阻尼增加不显著时,转子的跳动误差变化不明显,这表明气膜阻尼系数的增加抑制了气膜波动,使转子的跳动误差减小,同时,在空气静压主轴系统中,供气压强在0.3 MPa到0.5 MPa对转子振动影响显著。

图9 不同供气压强下转子跳动误差曲线
(3)从图10可以看出:随着主轴转速的增加,转子跳动误差减小;主轴转速从100 r/min增加到150 r/min时的跳动误差减小值与主轴转速从150 r/min增加到200 r/min时的跳动误差减小值相差不大;随着气膜阻尼系数的线性增加,转子的跳动误差趋于线性减小,这表明气膜阻尼系数的增加抑制了气膜波动,使转子的跳动误差减小。

图10 不同主轴转速下转子跳动误差曲线
4.2 气体轴承回转误差测量实验
主轴在实际工作过程中,气膜波动等气膜的动态特性会影响轴承和系统的动态特性。回转跳动误差是气体静压主轴动态特性的关键表征参数,直接影响主轴的加工精度和被加工件的表面形貌。通过回转误差测量实验可以探究气膜波动对主轴振动的影响和主轴跳动误差范围。如图11所示,实验采用JZ4511型精密气体主轴,以主轴轴线为基准,将精密测量半圆球安装在主轴顶部。在主轴工作过程中,通过电感式传感器,采用半径比较法进行回转跳动误差测量,振动信号由圆度测量仪信号调整箱采集和处理,通过电脑软件输出。

图11 气体轴承回转跳动误差测量试验台
经过理论讨论可知,无量纲气膜阻尼系数和主轴转速呈线性变化,同时,气膜阻尼的变化对理论跳动误差影响较为显著。因此,通过单一变量法改变主轴转速,从而得到不同气膜阻尼系数对应的转子回转跳动误差。该试验台气膜厚度为12 μm,空气压缩机对主轴系统的供气压力为0.5 MPa。
图12描述了转子在不同气膜阻尼系数下,考虑阻尼特性、不考虑阻尼特性以及实验的跳动误差值的对比。表2为相关结果的实验数据与仿真数据的对比。
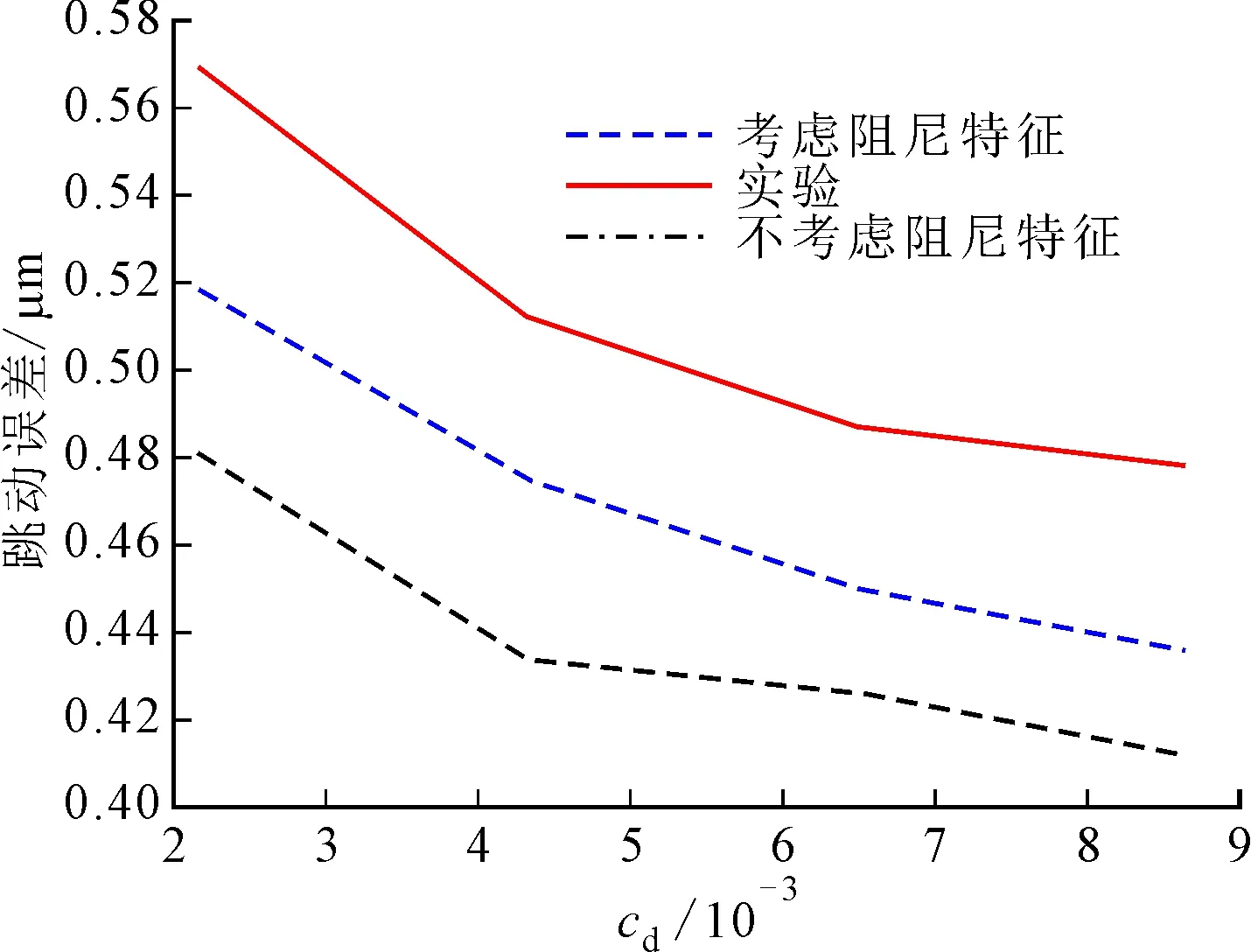
图12 转子跳动误差对比

气膜阻尼系数跳动误差/μm实验考虑气膜阻尼特性不考虑气膜阻尼特性0.002 160.5690.5180.4810.004 320.5120.4750.4340.006 480.4870.4500.4260.008 640.4780.4360.412
通过对比可以看出:随着气膜阻尼系数的增加,回转跳动误差有所降低,这与仿真结果规律一致,并且考虑阻尼特性下的误差值更接近实验测量值;考虑气膜阻尼特性的误差率分别为8.96%、7.23%、7.60%、8.79%,而不考虑气膜阻尼特性的误差率分别为15.47%、15.23%、12.53%、13.81%。因此,考虑阻尼特性时的气体轴承动态特性分析更准确。
5 结 论
本文建立了无量纲气膜阻尼模型,分析了气膜阻尼对轴承供气压强、主轴转速的影响规律和影响程度。通过建立轴承-转子系统模型,计算分析了各工况下转子跳动误差时域曲线。在轴承回转误差测量实验中,验证了考虑阻尼特性的误差值更加接近实验测量值。
(1)气体轴承的无量纲气膜阻尼系数随供气压强呈非线性增加,增加趋势先快后趋于平缓;随主轴转速呈线性增加,相较于供气压强,主轴转速对气膜阻尼影响更显著。
(2)气膜阻尼对气膜波动特性有抑制作用,适当地增加气膜阻尼系数可以提高主轴系统的稳定性。
(3)考虑阻尼特性的跳动误差率比不考虑阻尼特性减小了4.93%~8%,因此,考虑气膜阻尼特性可以更加准确的预测气体轴承动态特性和控制轴承的运动精度。
