高中数学函数零点解决方法探究

刘小龙

（巴中市第三中学，四川 巴中 636600）

一、根据函数图像解决函数零点问题

已知函数f(x)=logax+x-b（a＞0,且a≠1）,当2＜a＜3＜b＜4时，函数f(x)的零点x0∈（n,n+1）,n∈N*,则n=（）

[常规解法]：设f(x0)=0，因为f(x)=logax+x-b，又2＜a＜3＜b＜4，所以f(1)=loga1+1-b=1-b＜0

因为2＜a＜3＜b＜4，

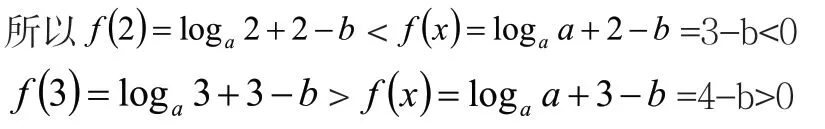
综上，x0∈（n,n+1），因此n=2

[图像解法]：在直角坐标系下分别作出y=log2x，y=log3x及y=3-x,y=4-x的图像，所有可能的交点构成了图中的阴影区域（不含边界），其中各点的横坐标都坐落在（2,3）以内，又因为x0∈（n,n+1），n∈N*，所以n=2。

要进一步强化学生针对零点问题的求法，掌握函数和方程之间的转化技巧，另外还要引导学生学会利用数形结合的方法来判断零点的个数，零点所在区间。在高考问题中，考查函数性质和方程根与系数关系的综合运用题一般难度较大，因此要在日常的学习中有所准备，加强训练。

二、利用零点性质求参数的取值范围

1.f(x)=x3-6x2+9x+a在x∈R上有三个零点，求a的取值范围。

解：由f'(x)=3x2-12x+9=3(x2-4x+3)=3(x-3)(x-1)得

令f'(x)＞0,得x＞3或x＜1,f'(x)＜0,

得1＜x＜3

所以f(x)在（-∞，1），（3，+∞）上单调递增，在（1,3）上单调递减。

所以f(x)极大值=f(1)=4+a＜0，a＞-4

f(x)极小值=f(3)=a＜0

所以-4＜a＜0.

2.方程x3-ax2+9x+a=0在[2,4]上有实数解，求a的取值范围。

解：由方程x3-ax2+9x+a=0在[2,4]上有实数解

即x3-ax2+9x=-a，

由f(x)=x3-ax2+9x的图像可得

0≤a≤4

3.x3-ax2+9x=0在[2,4]上有实数解，求a的取值范围。

在解决函数零点存在的区间或者方程根的个数问题时，主要采用的方法有函数零点定理和利用函数图象来进行判断。根据函数零点的性质，求参数的取值范围主要采用数形结合、等价转换以及分类讨论等方法。学生在解题过程中要注重利用导数求出函数的单调区间、画出函数的图象等方法，能够有效解决和零点相关的问题。