中等雷诺数方柱绕流的直接数值模拟及涡系分析

王建春，吴乘胜，王 星，徐金秀

（1.中国船舶科学研究中心 水动力学重点实验室，江苏 无锡214082；2.江南计算技术研究所，江苏 无锡214081）

0 引 言

湍流的数值模拟主要有雷诺平均数值模拟、大涡模拟以及直接数值模拟（Direct Numerical Simulation，DNS）三种方法，每种方法都有其重要的作用和地位，不可能被其他手段所完全代替。工程上研究湍流普遍采用的数值模拟方法是雷诺平均数值方法。这种方法的计算相对比较简单，但是获得的信息比较少，很难模拟到湍流的全部拟序结构；此外，它致命的缺陷是湍流模型不具有普适性。大涡模拟的主要思想是大尺度湍流涡系结构采用直接数值模拟方法求解，而小尺度湍流涡系结构则采用亚格子模型的方法来模拟；因而，其不足之处在于无法准确模拟小尺度涡系结构以及小尺度涡的耗散过程。

湍流数值方法中最准确的是DNS[1-3]。它不需要任何湍流模型，直接数值求解三维瞬态流动控制方程，能够捕捉到不同瞬时的湍流细致流场结构，因而可以了解湍流的精细流场、流动现象和流动规律等。DNS计算所得结果既可以用来深入研究湍流的流动结构，还可以用来检验和发展各种雷诺平均数值方法的湍流模型，检验大涡模拟的各种亚网格尺度模型以及检验湍流实验的测量精确度等。

制约DNS工程应用的关键瓶颈，在于其为了能够模拟所有尺度的湍流脉动以及各种尺度的拟序结构，求解算法需要具有非常高的时空分辨率，即数值模拟中需要足够多的时间步和足够精细的网格。通常对于充分发展的湍流，需要105以上的时间积分步，而网格的数量则随雷诺数呈指数增长。也就是说DNS所需的内存和计算量非常大，具有一定工程意义的中等以上雷诺数流动问题，需要使用超级计算机才能实现湍流的DNS模拟。

方柱绕流具有物体几何外形简单而流场结构非常复杂的特性，是钝体绕流研究的一种典型情况。将DNS用于柱体绕流的研究中，能够获得更加精细和准确的流场结构，无论是在理论研究上或是在工程应用上都非常有意义。一方面，柱体绕流中的涡激振动现象、流固耦合现象、尾涡的相互干扰现象都特别明显，复杂钝体绕流现象的研究一般都是基于柱体绕流而展开的；另一方面，柱形材料结构设计、船舶烟囱、房屋建筑和热交换器等设计，流动诱发的振荡[4]、声学辐射[5]、海底管道水动力性能[6]研究等都会涉及到柱体绕流的研究；在海洋工程中还有一些像钻井平台的立管等结构的绕流现象，也都可以采用柱体绕流的模型进行研究。近年来，伴随着计算机计算能力的提高，以及对一些新的现象比如展向渐变不稳定模型的认识的增加，都吸引了很多研究者的兴趣，其中包含了大量的柱体绕流的DNS研究[7]。

在此背景下，本文通过自主设计和编制的DNS并行计算程序，开展了中等雷诺数二维方柱绕流的DNS模拟研究。文中首先开展了低雷诺数流动（Re=100）的DNS模拟，以及数值模拟的时空分辨率收敛性研究，通过与文献结果的对比，对DNS程序进行了初步验证。随后在“神威·太湖之光”超级计算机上，开展了中等雷诺数流动（Re=10 000）的DNS模拟，对流动中的涡系发展及演化过程进行了分析，并通过与RANS和LES模拟结果的对比分析，展现了DNS在复杂精细流场模拟方面的优势。

1 控制方程及其离散

本文采用基于交错网格的有限体积法求解不可压缩N-S（Navier-Stokes）方程组，无量纲化积分形式控制方程组如下：

所谓的交错网格，就是压力、密度等物理量存储在控制体P的中心，这个控制体称为主控制体，如图1（a）所示；将速度分量（u,v）分别存储在主控制体的左右边线和上下边线位置处，再分别以此为中心，划分速度分量u和v的控制体，如图1（b）和图1（c）所示。

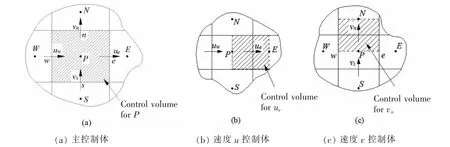
图1 交错网格示意图Fig.1 Description of staggered grid

离散后的方程组为：

式中各下标的意义为：e，n，w，s代表控制体的四条边，E，N，W，S代表控制体的中心位置，nb代表周围临近的节点。

数值求解中，压力-速度耦合采用SIMPLE（Semi-Implicit Method for Pressure-Linked Equations）算法[8]处理；离散得到的代数方程组采用Gauss-Seidel迭代求解；时间步进采用Euler隐式格式，对流项采用QUICK（Quadratic Upwind Interpolation of Convective Kinematics）格式，耗散项采用中心差分格式。具体离散求解过程可参考相关文献[9]。

数值求解过程中，控制方程组的收敛判据为：所有控制体中连续性方程余量的最大值小于规定值；动量方程的速度余量减少一个数量级或者迭代次数达到5次[10]；压力修正方程规定终止迭代时的范数与初始范数之比小于允许值。

2 并行算法

前面提到，DNS模拟所需的内存和计算量非常大，具有一定工程意义的中等以上雷诺数流动问题，需要使用超级计算机通过并行计算才能实现湍流的DNS模拟。

并行计算方法[11]可以分为三类：基于消息传递的方法、基于共享存储的方式和数据并行。基于消息传递的方法主要采用调用MPI函数库的方法，属于进程级大粒度并行；基于共享存储的方式主要采用Openacc编译制导指令的方法，属于线程级细粒度的并行。其中，MPI全称消息传递界面（Message Passing Interface）是目前使用较为广泛的并行计算处理方法。

在“神威·太湖之光”处理器架构上，采用相对比较多的是消息传递结合共享存储的方式。其中，MPI主要利用其主核来进行消息传递并行计算；而Openacc则利用其单个主核下的众核并行计算；二者的结合可以实现所谓的“二级并行”：进程间的并行+进程内部线程的众核并行。

本文的数值计算工作在“神威·太湖之光”超级计算机上开展，采用MPI[12]实现并行计算。之所以未采用MPI+Openacc二级并行，主要是因为本文采用的SIMPLE算法是一种半隐式的求解方法，压力修正方程往往需要采用隐式迭代算法如高斯赛德尔算法进行求解。此类隐式迭代算法的好处是收敛快，但这种算法本身实质上是串行的，存在数据相关性，暂时无法实现Openacc众核并行，虽可采用红黑着色法代替之，但一定程度上使得迭代方法半显式化了，导致计算收敛变慢，效果并不好。

MPI并行方法又可以分为数值算法并行和区域分解并行，目前使用较多的是后者，其基本的工作原理如图2所示：图中将一个大任务分解为多个子任务，每个子任务分配给一个进程；进程间的信息传递主要是将边界处的值进行交换或者插值处理，如图中进程5就需要同时与周边四个进程进行边界信息传递。图中：MX是水平方向上的最大网格数，0、-1、MX+1和MX+2代表了用于交换信息的虚拟边界。

图2 MPI区域分解并行过程示意图Fig.2 Description of MPI domain decomposition for parallel computation

3 低雷诺数方柱绕流DNS模拟与分析

3.1 方柱绕流的物理几何模型

图3给出了二维方柱绕流的几何模型，其中采用四个参数x1=11.1d，x2，y1，y2来确定方柱的具体位置；L=36d为计算域长度，H=100/7d为计算域宽度，d为方柱长度。AB为进口、CD为出口、BC为上边界、AD为下边界。

边界条件定义如下：

入口处（AB）的边界条件为均一来流，给定速度分量的大小：U=1，V=0。

出口边界距离柱体足够远，此时出口处的流动状态达到充分发展状态，在流动方向上各参数梯度变化为0，即出口处应为平滑流动。这里定义速度沿CD边界法向变化为0，即∂U/∂n=0，∂V/∂n=0，n为界面法向。

对于物面边界采用的是固壁边界条件，固壁的速度边界条件一般为无滑移边界条件，即U=0，V=0。

上下边界条件为轴对称面边界条件：流动的法向速度为零，而切向速度不应该存在速度梯度，也就是V=0，∂U/∂y=0。

图3 二维方柱绕流的物理几何模型Fig.3 Physical geometry model of flow past a two-dimensional square cylinder

所有的压力边界条件都采用Neuman边界条件。

3.2 低雷诺数方柱绕流DNS模拟及时空分辨率收敛性分析

为验证计算程序，首先开展了低雷诺数（Re=100）方柱绕流DNS模拟研究，分别开展了计算的时间和空间分辨率收敛性研究。

（1）时间分辨率收敛性研究

图4 不同时间步长方柱升力系数时历曲线（Re=100）Fig.4 Time history of lift coefficient for different time step(Re=100)

图5 不同时间步长方柱阻力系数时历曲线（Re=100）Fig.5 Time history of drag coefficient for different time step(Re=100)

图4给出了网格数为672*300（空间分辨率为0.05，满足Re=100时的DNS模拟要求）、时间步长分别为0.002 s、0.001 s和0.000 5 s时的方柱升力系数时历曲线；图5则给出了该网格下不同时间步长的方柱阻力系数时历曲线。

从图中可以看出，对于Re=100的方柱绕流，在该网格下，当时间分辨率达到0.001 s时，计算结果已经收敛了。

（2）空间分辨率收敛性研究

分别采用空间分辨率0.071、0.05和0.04的三套网格（对应的网格数分别为450*200、672*300和810*355）进行网格收敛性研究，时间步长根据前面的研究取为0.001 s。

图6和图7分别给出了不同空间分辨率时方柱升力系数和阻力系数时历曲线。从图中可以看出，当空间分辨率达到0.05时，计算结果是收敛的。

图6 不同空间分辨率方柱升力系数时历曲线（Re=100）Fig.6 Time history of lift coefficient for different spatial resolution(Re=100)

图7 不同空间分辨率方柱阻力系数时历曲线（Re=100）Fig.7 Time history of drag coefficient for different spatial resolution(Re=100)

表1给出了程序计算收敛后获得的计算结果与相关文献的对比。由表1和图7可见，在Re=100时，计算所得方柱平均阻力系数为1.48，与Sohankar和Davision等人[13-15]计算得到的结果基本一致；而St数却存在一定的偏差，主要原因可能是由于时间离散采用一阶全隐格式，离散精度不够高。

表1 计算结果与文献的比较（Re=100）Tab.1 Comparison between computed results and the reference(Re=100)

图8给出了一个周期内尾流场中的卡门涡街变化过程。从t=180 s到t=189 s，方柱尾流中的漩涡完成一个周期下的运动，尾涡的变化过程如下：右下角产生新的小涡→右下角的小涡增大的过程中，右上角的大涡脱离壁面并向后方迁移→右下角小涡变成大涡→右下角大涡开始脱离壁面并向下游迁移，右上角产生新的小涡→右上角小涡增大变成大涡、大涡开始脱离壁面并向下游迁移→右下角产生新的小涡。

通过以上低雷诺数方柱绕流DNS模拟及时空分辨率收敛性分析可知，计算程序的设计编制是正确的；在满足DNS要求的时空分辨率情况下，计算结果是准确可靠的。

4 中等雷诺数方柱绕流DNS模拟与涡系分析

对Re=10 000的二维方柱绕流进行了DNS模拟，计算域根据文献[17]确定：x1/d=5，L/d=21，H/d=11.4；数值模拟中，时间步长取为0.000 5 s，空间分辨率为1.0/70（网格总数103万），满足DNS模拟对时空分辨率的要求。

4.1 升力及平均流场计算结果

图9给出了方柱升力系数的时历曲线（部分）。从图中可以看出，升力系数随时间的变化不再具有明显的周期性。将升力系数进行频谱分析可以得出无量纲参数St数；从图9右侧的频谱图可以看出，数值模拟得到的St值为0.128，与实验[15]结果St=0.130基本一致。

图9 方柱升力系数时历曲线图及其频谱图（Re=10 000）Fig.9 Time history of lift coefficient and corresponding frequency spectrum

图10左侧给出了经过77 s统计平均后得到的上表面水平速度平均值的分布云图，右侧给出了三个位置上的平均水平速度沿垂向的分布（上）及与文献[17]计算结果（下）的对比。

由图中可以看出：①本文计算得到的方柱上表面的平均水平速度分布与文献[17]的计算结果基本一致；②分离泡的外缘的平均速度剖面类似自由剪切层；③一个大的回流区几乎覆盖了方柱整个上表面；④x=-0.4～0.3之间（方柱前角点后方），有一个明显二次回流区域。上述流场特征，都和文献[17]中的计算结果完全一致。

4.2 涡系结构分析

图11给出了t=105 s时刻，本文计算得到的流场涡系结构（下）与文献[17]计算结果（上）的对比。从图中可以看出，对于方柱尾流场特征及涡系结构，本文计算结果与文献[17]中的基本一致：在紧邻柱体后方的流场中，形成很多的小尺度涡和涡丝，这些小尺度涡和涡丝相互融合形成大涡并与其他大涡相互作用使其破裂成小尺度涡和涡丝；在远离方柱的地方，这些小尺度涡和涡丝通过融合的方式形成相对比较稳定的流场结构，比如图中所示的单极子型涡和偶极子型涡。

图10 方柱上表面平均水平速度云图及速度分布曲线图Fig.10 Mean u-velocity contour and profiles for three locations along upper side of cylinder

图11 流场涡系结构计算结果与文献[17]的对比（t=105 s）Fig.11 Comparison of vortex structures for the computed results and the Ref.[17](t=105 s)

图12给出了更为细致的流场涡系结构图（t=105s）。从图中可以看出，DNS模拟很好地捕捉到了钝体绕流的典型流场结构和特征，如：分离泡，伪三角区，单极子型涡、双极子型涡的形成和迁移过程，以及小尺度涡的耗散过程等。

分离泡[16]是一种在航空航天以及其他工程领域中都广泛存在的转捩现象：在中低雷诺数下，流动常处于层流状态；当流体流过柱体前缘后，由于其抗拒逆压梯度的能力较弱，容易产生分离；层流分离后，剪切层离开壁面，由于速度剖面不稳定，很快导致转捩；转捩后的湍流裹入能量使边界层再附着，从而形成分离泡。

伪三角区是指方柱前缘分离泡和由主涡诱导产生的二次涡构成的形状类似三角形的区域。伪三角区域是钝体绕流动力学的基础流动结构，属于一类相对较稳定的流场结构。所谓稳定是指：在伪三角区域内，大部分区域都是吸附在固体壁面上的，尽管它会振荡和变形，但是二次涡形状无论在时间还是空间上都是定常的，分离泡则有规律地在最大和最小距角之间轻微地变化。

图13给出了t=105-108 s时段方柱绕流涡量场的变化过程。从图中可以清楚地看出各种涡的形成、脱落、发展、迁移和耗散等过程：

图12 流场细观涡系结构（t=105 s）Fig.12 Meticulous vortex structure in the flow field(t=105 s)

图13 方柱绕流涡量场变化过程（Re=10 000）Fig.13 Description of the vortex contour changing with time simulated by DNS(Re=10 000)

在Re=10 000情况下，涡开始从侧边发生脱落，但并不是从分离点发生脱落的，而是从紧邻伪三角区域后方的主涡的顶部发生脱落的。

在柱体后面的流场中，会形成很多的小尺度涡和涡丝。这些小尺度涡和涡丝会在远离方柱的地方，通过融合的方式形成相对比较稳定的流场结构，如单极子型涡和偶极子型涡。随着流体的迁移运动，单极子型涡和偶极子型涡在迁移过程中基本形态不会发生变化，偶极子涡中的两个大小相等的对称反向涡相对位置保持不变。这说明在流场中，单极子和偶极子型涡是比较稳定的流动结构；相对而言，流场中的其它类型的涡则较不稳定，往往会因为相互间的作用发生变形甚至破裂，比如在流场内的各种涡量大小不对等的涡结构。

Re=10 000的方柱绕流尾流中，涡的相互作用非常剧烈，特别是大涡与小涡之间的相互作用，在这种作用下往往会触发大涡的破裂以及再形成。大涡的破裂是因为在其迁移过程中，由于迁移速度较快与后方迁移速度较小的涡发生了碰撞，破坏了大涡的稳定性；原先的大涡发生了破裂，破裂后形成了一个较小的涡核以及很多的涡丝；小的涡核继续向着下游迁移并由于涡核的吸引作用，不断地发展变大，最后会形成新的单极子型涡；涡丝则有一部分会耗散在流场中，另一部分会被涡核吸附形成新的大涡。

在方柱下表面也明显发生了涡的破裂现象，破裂后的涡一部分向下游迁移，另一部分则吸附到柱体表面上。这种涡的破裂是因为方柱下表面层流发生转捩所致。

图11-13也展现了小尺度涡的耗散过程。该耗散过程主要是由于人工粘性和数值耗散引起的，其机制与能量的耗散相似，因而一定程度上能够反映出小尺度涡的能量耗散过程：从105 s时刻开始，顺时针旋转涡和逆时针旋转涡的涡量幅值是相等的；在106 s、107 s瞬时，逆时针旋转涡的涡量幅值保持不变，而顺时针旋转涡的涡量幅值则逐渐变小；最后涡量幅值逐渐趋于0，流场中已经不能清晰地看到该涡结构。这个过程就是小尺度涡的能量耗散过程。

4.3 DNS、RANS及LES模拟结果对比

由于DNS模拟计算量巨大，因而本文也尝试采用计算量相对较小的RANS和LES方法，开展方柱绕流（Re=10 000）的数值模拟，研究这两种方法能否准确模拟此类复杂精细流场。

图14给出了采用RANS方法模拟得到的Re=10 000方柱绕流的涡量场及其变化过程（t=105-108 s），其中湍流采用SST k-ω模型处理。

图14 方柱绕流涡量场RANS模拟结果（Re=10 000）Fig.14 Description of the vortex contour changing with time simulated by RANS(Re=10 000)

从图中可以看出，相比于DNS模拟，RANS模拟有以下几点不足之处：

（1）只能捕捉到一些较大的涡结构，无法获得典型的钝体绕流场基本结构特征，例如伪三角区域和分离泡结构等；

（2）在尾流场中没有不同尺度的涡结构，也就无法模拟小尺度涡是如何耗散的过程；

（3）涡的脱落只发生在尾流场中，而不是出现在方柱上表面的伪三角区域后方。

以上对于流场特征及涡系结构的分析，说明RANS方法无法准确模拟诸如方柱绕流之类的复杂精细流动。

图15给出了采用LES方法模拟得到的Re=10 000方柱绕流的涡量场及其变化过程（t=105-108 s），其中亚格子模型采用Smagorinsky-Lilly模型。

从图中可以观察到LES模拟与DNS模拟结果有一些相一致的现象：如涡的脱落不是在方柱前缘的分离点而是在靠近伪三角区域后方的顶端附近；在t=106 s时刻，下表面的大涡也发生了破裂现象等。

但相比于DNS模拟，LES模拟得到的尾流场中的涡结构不稳定，很容易随着流动发生各种拉伸和变形，没有相对稳定的单极子型涡和偶极子型涡结构。这也就是在复杂精细流场模拟方面，DNS相比于LES的更具优势的表现之一。

图15 方柱绕流涡量场LES模拟结果（Re=10 000）Fig.15 Description of the vortex contour changing with time simulated by LES(Re=10 000)

图16给出了DNS、LES和RANS三种数值模拟方法计算获得的方柱升力系数时历曲线。从图中可以看出：

图16 方柱升力系数时历DNS、LES和RANS计算结果（Re=10 000）Fig.16 Time history of lift coefficient computed by DNS,LES and RANS(Re=10 000)

RANS数值模拟得到的方柱升力系数时历曲线具有明显的周期性，周期约为6.5 s（St=0.154）。然而文献[15]指出，对于方柱绕流，当Re＞1 000时流动就已经不再是层流状态了。因此Re=10 000时，柱体表面的涡脱落过程不再具有固定的周期，从而升力系数也不应该是周期性变化的，这与RANS模拟的结果是矛盾的。由此可见，采用RANS方法模拟该雷诺数下的方柱绕流，其流场模拟结果是不准确的。

对于LES和DNS模拟，计算得到的方柱升力系数时历曲线都是不规则的，没有表现出明显的周期性，无法直接比较，因而通过对升力系数时历曲线的频谱分析，得到无量纲参数斯特劳哈尔数（St），从而便于比较。

图17给出了LES和RANS数值模拟得到的方柱升力系数时历曲线的频谱分析。表2给出了频谱分析得到的St，表中同时给出了实验结果。从表中可以看出，DNS模拟得到的St与实验结果最为接近。这也意味着对于方柱绕流（Re=10 000）这类复杂流动，DNS模拟最为准确。

表2 不同计算方法得到的StTab.2 St computed by different methods

图17 LES和RANS计算得到的升力系数频谱图Fig.17 The corresponding frequency spectrum of lift coefficient computed by LES and RANS

5 结 论

本文通过自主设计和编制的DNS并行计算程序，在“神威·太湖之光”超级计算机上，开展了中等雷诺数二维方柱绕流的DNS模拟研究。通过对流动中涡系发展及演化过程的分析，以及与RANS和LES模拟结果的对比分析，可以得出以下结论：

（1）通过低雷诺数（Re=100）方柱绕流DNS模拟及时空分辨率收敛性分析可知，计算程序的设计编制是正确的，且在满足DNS要求的时空分辨率情况下，计算结果准确可靠；

（2）对于中等雷诺数（Re=10 000）方柱绕流，本文的DNS模拟成功地捕捉到钝体绕流的典型流动现象和特征，如：涡街的形成和脱落，分离泡的产生和变化，伪三角区的形成，一些特有的稳定流场结构如单极子型涡与偶极子型涡的形成和迁移，以及小尺度涡的耗散等；同时，对于方柱尾流场特征及涡系结构的模拟结果，与公开发表文献的结果基本一致；

（3）与RANS和LES的中等雷诺数（Re=10 000）方柱绕流模拟结果相比，无论是流场特征、涡系结构等流动细节，还是方柱升力系数时历和主涡脱落频率（St）等宏观量，DNS模拟结果都明显更为准确，体现了DNS在复杂精细流场模拟方面的优势。

致谢：本文的研究工作得到了中国船舶科学研究中心张楠研究员的大力帮助和启发性指导，以及江南计算技术研究所的徐占工程师、陈德训高工、刘鑫高工等人的技术支持。对于他们的无私帮助和对论文的贡献，作者在此表示由衷的感谢！