探究性学习让数学教学更有意义

☉江苏省张家港市暨阳高级中学 王晓英

生命的河流始终会往其理想的海洋奔去，但其奔向大海的过程却也往往充满荆棘，这就好比人的一生，困难与挫折随时会出现在我们的人生之中，但满怀理想的人生也必然会有惊喜出现.传道、授业、解惑是人民教师在青少年成长过程中必须担负起的责任，引导学生在现在学习、将来圆梦的信念支撑下学习和成长，使学生在渗透哲理的学习中掌握知识和技能，当然这也需要教师及时将教学方式和学习方式进行改进并引领学生的成长.

学习过程中不能积极思考并发现问题的学生往往是被动的，这部分学生在学习领域中往往不能视作学习的擅长者，学习过程中往往也无法表现出具有创造性的学习行为.因此，教师在实际教学中应特别注重启发学生发现问题，并提出问题，使学生的学习兴趣得到有力的激发，引导学生在有意义的阅读与思考中加深自己对学习内容的理解并顺利构建出相关的数学问题，学生学习数学、运用数学的意识一旦得到有效的刺激和提升，一定会在学习中产生更多有意义的思考.学生在有意义的思考与探索中也会越发感受到数学学习的亲近感并树立学好数学的自信心，这对于学生的学习生涯乃至一生都会产生至关重要的影响.

一、引导学生在探究、实践、合作交流中体验快乐

探究性学习这一认知方式对于学生来说其实是与生俱来的，学生在现实的数学活动中理解数学知识、思想与方法能够令其掌握得更加深刻且牢固，单纯依赖教师讲解的数学学习活动对于很多学生来说都是走马观花.学生在亲历实践、自主探究、合作探究的学习过程中往往能够获得亲身体验的成功与快乐，这种重要的学习方式与新课程理念所提倡的“做数学”是相吻合的，学生在亲身体验的过程中经历并探究数学能使数学课堂真正成为学生探究数学的阵地.事实上，教材中就存在很多蕴含数学重要思想方法与探究理念的例题与习题，这些重要资源的充分利用能够使学生在亲历探究的过程中获得实践的成功与快乐，并在脑海中留下独到且牢固的印象.

例1如图1所示，在平面直角坐标系xOy中，直线l：y=x+m与x轴、y轴分别交于点A和点B（0，-1），抛物线经过点B，且与直线l的另一个交点为C（4，n）.

（1）求n的值和抛物线的解析式；

（2）点D在抛物线上，且点D的横坐标为t（0＜t＜4）.DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）.若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值.

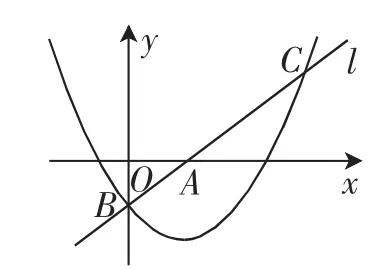
图1

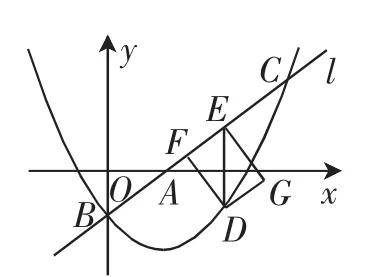
图2

即将参加高考的高三学生若想在此题上立即得出结果是有一定难度的，因此，教师在给出此题之后应给予学生充分的思考空间，很多学生在充裕的思考之后都会产生跃跃欲试的情感.

所以m=-1.

所以直线l的解析式为

在Rt△OAB中

因为△OAB∽△FDE，所以所以DE.所以p=2（FD+

因为D点的横坐标为t（0＜t＜4），故点D的坐标为，点E的坐标为且0＜t＜4，

所以当t=2时，p有最大值

二、在拓展中培养学生的学习自信心

在类比、引申、推广中提出新问题并解决新问题，不仅能帮助学生有效地巩固基础知识，还能帮助学生树立积极探索与创新的精神，并因此帮助学生树立数学学习的自信心.比如以下习题的拓展与延伸.

例2证明：（1）若（fx）=ax+b，则

（2）若（fx）=x2+ax+b，则

教师在这一习题的教学中应注意结论证明之后的拓展和延伸，笔者在此题的教学中就进行了如下的设计：将（2）中的条件进行改变并探求其结论，大家是否能将所获得的新命题进行推广呢？笔者在问题设计之后又对学生进行了引导，预留了充足的时间供学生思考，并启发学生大胆变更条件、探索结论、推广命题，最后请学生将自己的探究成果进行了展示.

生1：若（fx）=ax2+bx+c（a＞0），则若f（x）=ax2+bx+c（a＜0），则f

师：不错，大家勇于探索和创新的精神令老师由衷的高兴，大家以后必然能为我们国家作出应有的贡献.学生在集体讨论与探索中也再一次进行了有关结论的推证并达成了共识.之前的讨论中，生1、生2、生5是对的，但生3和生4错了，大家能对两个错误的结论进行修正吗？

生6：将生3的结论这样修正：若f（x）=ax（a＞0且a≠1），都有

生7：将生4的结论这样修正：若f（x）=logax（a＞0，且a≠1），对任意x1，x2∈（0，+∞），当a＞1时，有；当0＜a＜1时，有

师：很好，大家对比对数函数的结论试试看，可有什么发现呢？引导学生在探究最酣之时进行规律的总结并得出凸函数的性质：

如果定义在区间I上的函数y=f（x）为下凸函数，那么对于任意x1，x2∈I，则有

如果定义在区间I上的函数y=f（x）为上凹函数，那么对于任意x1，x2∈I，则有

高中数学课程引入的数学探究这一新的学习方式对于学生的数学学习来说具有积极的意义，能帮助学生在了解数学概念、结论产生的过程中对其直观与严谨的关系形成更好的理解，使学生能够在亲身经历数学研究的过程中体验到创造的激情并养成严谨的科学态度，使学生在勇于探索与创新的学习过程中养成质疑与反思的意识和习惯，使学生在不断发现问题、提出问题、解决问题的过程中养成不怕困难的科学精神，并对学生创新意识的发展和实践能力的提升起到积极的助推作用.