高中数学教学中培养直观想象素养的策略研究

☉江苏省张家港市塘桥高级中学 汤 鸿

☉江苏省张家港市塘桥高级中学 钱士明

在教育部公布的相关政策中指出，教育改革及推进的关键任务在于加强对学生数学核心素养的培养及对教学质量的保障.高中数学课程标准修订组依据普通高中课程修订工作的要求，提出教书育人的关键在于对学生核心素养的培养.直观指的是对于事物的感性认识，是经过对实际实物的直接接触而获得的；想象指的是经过加工改造在人的脑海中塑造出新形象的过程.所以，“直观想象”的定义就是利用空间想象及几何直观来对事物的变化进行感知，借助图形进行数学题目的解答.那么怎样在教学过程中对学生的直观想象素养进行有效的培养呢？这是我们需要重视的一个问题.

一、加强概念教学

熟悉数学概念是进行数学思想学习的载体，并且“直观想象”思想在很大程度上都来自于数学中的概念教学过程.在这个过程中，要有意识地赋予抽象的概念一个具体的“形”，让学生能够很好地理解概念，这样学生才能够在题目的解答过程中对概念运用自如.比如，在进行“函数”这一章知识的学习过程中，学生对于函数的概念及其性质难以把握，因此教师可以引导学生从“形”的角度进行理解，从而让学生能够更加容易地掌握其定义.

例1已知定义在R上的奇函数f（x）在（0，+∞）上单调递增，且f（1）=0，则不等式f（x）＞0的解集为______.

图1

根据题意作出函数的图像，如图1所示，易得解集为（-1，0）∪（1，+∞）.

教师在进行数学教学时，要注重对于概念的讲解，将一些性质的不同表达形式讲授给学生，让学生能够全面地掌握数学性质.在今后的解题过程中，不管概念的表达形式如何变化，学生也能够灵活的运用.

二、教学充分展现直观想象的魅力，激发学生的学习兴趣

在学习一元二次不等式的过程中，运用直观想象的教学方法，能够体现直观教学法在解答数学问题时的便利性，让学生能够从变化、运动及联系的角度对问题进行思考.

例2设m∈R，解关于x的不等式mx2-（m+1）x+1＞0.

不等式化简为（mx-1）（x-1）＞0，若转化成

（1）若m=0，易得解集为（-∞，1）.

（2）若m≠0，则（fx）与x轴交点的横坐标分别为和1.

①当m＞0时，根据和1的大小关系可知（fx）的图像有以下三种情形：

图2

图3

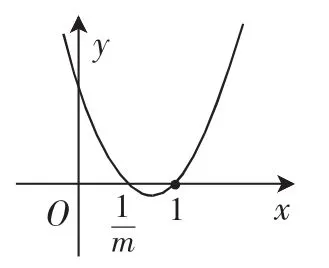
图4

图5

可知当0＜m＜1时，如图2所示，其解集为（-∞，1）∪

当m=1时，如图3所示，其解集为（-∞，1）∪（1，+∞）；

当m＞1时，如图4所示，其解集为

②当m＜0时，f（x）的图像只有一种情形，如图5所示，其解集为

通过对一元二次函数图像的观察，了解不等式的具体性质，再通过不等式和图像之间的关系，进行相关问题的解决.让学生能够根据“形”的运用，体会其对数学难题解答的便利性.这个时候再向学生讲解“最高次系数化正后，大于零取两边，小于零取中间”，这样学生就能够更加容易理解这句话的具体含义了.

三、培养观察、联想、猜想能力

联想是根据当前的具体事物，联想到与这件事物相关的其他事物，在这一过程中对学生联想能力的培养具有很大的帮助.在很多数学问题中，可以采取想象的方式，将数学问题转化成“形”.通过对学生的数学联想能力的培养，使其发现数学的“数”与“形”之间的关联，并进行数形之间的相互转化.

例3当n∈N*时，比较2n与n2+2n的大小.

图6

思路很清晰，从1开始代入比较大小，然后进行归纳猜想，再用数学归纳法进行证明.可以发现，从1到5都是2n＜n2+2n，但如果由此猜想2n＜n2+2n就错了，实际上从6开始都是2n＞n2+2n.如果作出x＞0时f（x）=2x与g（x）=x2+2x的图像，在图像的走势上，我们可以先预判，最后一定是2x要比x2+2x大，这样就不难发

现在交点B的右侧f（x）=2x的图像处于g（x）=x2+2x的图像的上方.

因此结论应该是：当n≤5时，2n＜n2+2n；当n≥6时，2n＞n2+2n.

猜想是根据一些事实进行合理推断的过程，是一种综合性较强、复杂程度较大的认知过程，猜想的前提是对事物进行合理的推断.在学习数学归纳法及数列的基本知识的过程中，采用猜想论证的形式，不仅能够简化知识点的难度，还能够激发学生学习数学的兴趣，从而加强数学学科对学生的吸引力.

四、利用多媒体教学，展示直观想象

在对“数”与“形”之间的关系进行讲解时，可以采用多媒体教学的方式，让学生更加直观的了解.例如，可以采用《几何画板》，让“死图”变“活图”.在学习圆锥曲线的过程中，利用多媒体教学，向学生展示数的变动带来形的变化，这样能够更好地加强学生对于知识的理解，使学生对知识的记忆变得更加的牢固.

例4（2014年江苏卷的应用题）如图7所示，为保护河上古桥OA，现规划建一座新桥BC，同时设立一个圆形保护区.规划要求：新桥BC与河岸AB垂直；保护区的边界为圆心M在线段OA上并与BC相切的圆，且古桥两端O和A到该圆上任意一点的距离均不少于80m.经测量，点A位于点O正北方向60m处，点C位于点O正东方向170m处（OC为河岸）

（1）求新桥BC的长；

（2）当OM多长时，圆形保护区的面积最大？

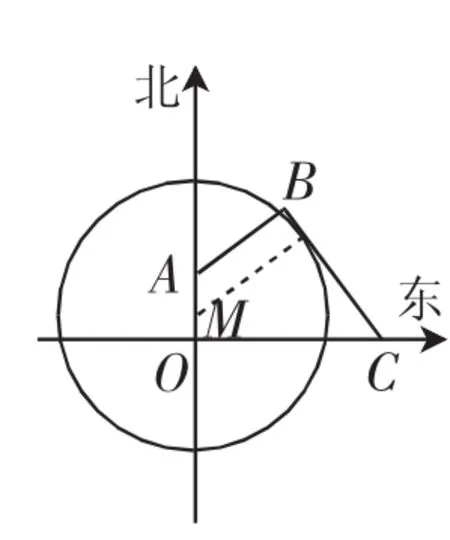
图7

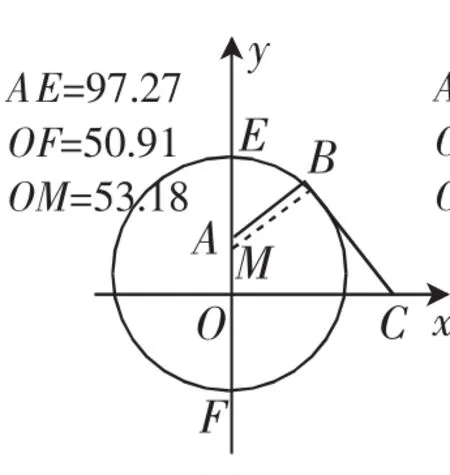
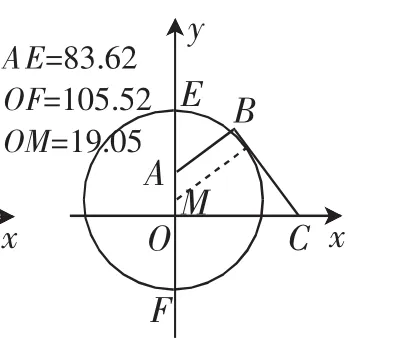
图9

在解决第（2）问时，利用几何画板可以发现，当M从A向O移动时，半径和OF是越来越大，AE越来越小.而AE和OF需都满足不小于80m，故AE为80m即可，此时利用ME等于M到BC的距离即可求得OM=10m.

五、逐步培养学生的直观想象能力

在对直观想象能力培养的过程中，要根据学生学习的具体情况进行，不能急功近利.在高一时，学生所碰到的题目类型较少，因此在这个时候学生处在尝试探索的阶段.如果这时候将直观想象思想灌输给他们，会让学生失去学习的兴趣.而当学生已经积累了一些主要的知识，逐渐感受到这种思想方法的优点时，教师再进行具体的介绍，通过专题讲座的形式将该方法传授给学生，这时候学生会更加容易理解并掌握.

例5已知函数若函数g（x）=f［f（x）］-m有三个零点，则实数m的取值范围是______.

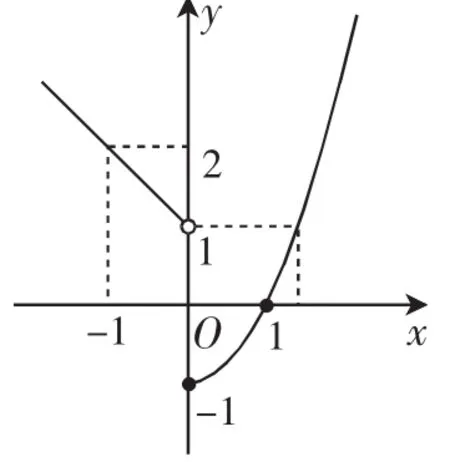
图10

设f（x）=t，则由g（x）=0得f（t）=m.作出函数f（x）的图像，如图10所示，则当-1≤t≤1时，满足f（x）=t的x有一个解；当t＞1时，满足f（x）=t的x有两个解.

因此要使g（x）有三个零点，则满足f（t）=m的t应有两个解，即t1∈［-1，1］，t2∈（1，+∞），则m∈（1，2］.

综上所述，对于数学核心素养的学习是数学教学中的重要内容，既需要在理论层面上进行学习改进，还需要在实际教学过程中进行完善.在进行数学核心素养的培养过程中，应当探索其有效的培养途径，加强对直观想象能力的合理教学，最终使学生深入地学习数学核心素养的理论知识.