课标下高中数学习题教学的研究

☉江苏省连云港市城南高级中学 秦 名

高中习题教学已经成为现阶段教师在课堂教学中的一种方式.本文主要探索如何在高中教学的过程中发挥学生的主体性，提高课堂教学效率，使数学习题教学更有意义.

一、高中数学习题教学方式的创新转变

在进行习题教学的过程中要注意调动学生的积极性，同时加强教师与学生之间的互动.在学生解题遇到困难时，教师应当细心地进行讲解，并让学生了解到自身存在的问题，让学生在这个过程中能够进行自我反思、自我总结.同时我们在对数学题目进行解答的过程中可以采用信息技术加以辅助.从而使课堂教学的结构更加完整，同时适量地扩展课堂教学的内容，让学生的课堂效率得到极大的提高.在解答立体几何的有关问题时，可以采用信息技术来进行题目的展示，使原先较为传统的教学方式变成创新型的教学方式，将数学的抽象性转化成较为形象的图式，从而让数学的学习充满趣味性.比如将立体几何或解析几何习题通过信息技术来进行生动且形象的演示，令传统的学习方式转变成一种创新型的方式.

例1如图1，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=a，E是SD上的点，且DE=λa（0＜λ≤1）.

（1）求证：对任意的λ∈（0，1］，都有AC⊥BE；

（2）若二面角C-AE-D的大小为60°，求λ的值.

图1

在此题中，λ为未知量，因此E是SD上的动点，若单独看习题中的图示，很多学生会认为点E此时是特殊点，并且看不出当E点变化时，都有哪些线段跟着变化.因此，运用多媒体软件进行题目的展示既能丰富课堂活动，活跃课堂气氛，又可以使学生更加直观地理解题目内容，如图2.

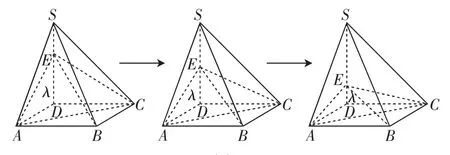
图2

例题答案：（1）连接BD，由底面ABCD是正方形可得AC⊥BD.

因为SD⊥平面ABCD，所以BD是BE在平面ABCD上的投影，由三垂线定理可得AC⊥BE.

（2）因为SD⊥平面ABCD，CD⊂平面ABCD，所以SD⊥CD.

又底面ABCD是正方形，所以CD⊥AD.又SD∩AD=D，所以CD⊥平面SAD.

如图3所示，过点D在平面SAD内作DF⊥AE于F，连接CF，则CF⊥AE.

故∠CFD是二面角C-AE-D的平面角，即∠CFD=60°.

在Rt△ADE中，因为

在Rt△CDF中，由

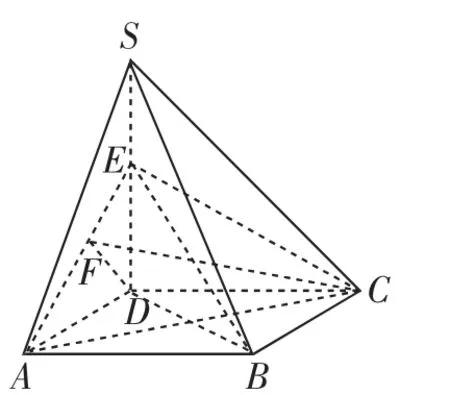
图3

再者，采用这种创新的习题教学方式还能够减少老师在黑板上列公式、画图的时间，让老师能够在课堂上教授更多的知识.在教学实践中我们要充分应用教学设备，将教学重心放在对题目的动态探索上.利用当代教学设备的先进性及便利性，使数学习题在数量及质量上得到更好的提升，使学生能够产生强烈的学习兴趣.我们在进行习题训练的过程中要注意对习题进行变形，让学生能够举一反三，同时锻炼学生的想象力及联想能力，从而不断提升学生的数学思维能力及科学探索能力.

二、以问题引导高中数学习题教学，让学生形成创新意识及问题意识

问题教学能够让学生进行深入的思考，同时让教师的教学方式更加的完善.所以我们要在教学时采用以问题来引发思考的方式，创设相关的情景教学.让学生的学习思维及学习方式得到发展，同时激发学生的好奇心及求知欲，从而让学生的学习能够在兴趣的驱使下进行.在学生已经熟练了解知识体系的基础上，让学生进行习题训练，使他们感受到对于知识的学习并不是通过死记硬背得到的，而是通过自身的理解消化才能够对知识进行全面的掌握.当然，对于学习能力的锻炼还需要以扎实的知识及稳固的能力结构、灵活的学习思维为基础.所以，在进行习题教学的过程中，要让学生掌握正确的审题方法，仔细的审题，并且进行正确的评讲，从而让学生形成全面的信息处理能力.比如在进行人教版高中数学A版教材的学习时，在对每一课的内容进行引入时，可以以问题的形式进行展开，让学生通过对问题的思考来引入本节课的教学内容.通过推理观察、探索思考等方式，让学生自主寻找习题的答案，获取最佳的解决方式，从而领会到数学思想的内涵.

三、合理启发、创新数学思维，促进高中数学习题教学水平的全面提升

在进行习题教学的过程中，高中数学教师要将猜想思维渗透其中，让学生能够灵活地运用自身的想象.将课本中固定的习题模式转化为开放性的数学问题，从而为学生创设良好的学习氛围及热烈的讨论环境，让学生能够形成敢于质疑、敢于猜想的能力.比如，在进行习题训练时，我们可以让学生从不同的角度，采用不同的方法来对某个问题进行解答，从而让学生能够形成发散思维，让学生在今后的解题过程中能够形成更加清晰的解题思路.在进行题目训练时，可以尝试培养学生运用逆向思维法、反证法、倒解法等一系列方法.同时注重对学生实践能力的培养，让学生敢于提出质疑，并发表自身见解.比如，在进行圆的方程这一课的内容学习时，可以采用这样的例题：

例2圆x2+y2-2x=0和x2+y2+4y=0的位置关系是（ ）.

A.相离 B.外切 C.相交 D.内切

解析：将两个圆的方程分别化为标准方程（x-1）2+y2=1，x2+（y+2）2=4，两圆圆心及半径分别为O1（1，0），，又，所以两圆相交，故答案选C.

通过例题来引出学生对该内容的掌握情况.首先可以让学生自己先进行题目的解答，在解答的过程中学生会发现使用标准方程进行求解太过复杂，因此学生会对这种方式产生质疑.这时候教师可以鼓励学生尝试用更加简单的方法进行求解，通过学生之间的交流讨论，从而得到使用相关的直线知识求解方程的方法可使解题的步骤更加的简单.教师可以接着提问，让学生探究是否还有其他的解决方法，从而引发学生进一步的思考，加深学生对圆的相关知识的印象.

四、结束语

高中数学习题教学法可以帮助学生形成自主学习、深入探索的良好习惯，从而提高学生的数学学习素养，加强师生之间的沟通交流.所以在进行教学的过程中要充分利用习题教学的优势，提高学生的数学学习兴趣，提升学生的数学综合水平.