彰显过程分析 考查科学思维
——液柱移动问题的解决策略
2019-08-20陈庆炜朱广天
陈庆炜 朱广天
(华东师范大学教师教育学院 上海 200062)
新修订的《普通高中物理课程标准》将三维目标修改为物理核心素养, 明确指出了物理学科核心素养包括物理观念、科学思维、科学探究、科学态度与责任4个方面. 其中科学思维是基于经验事实建构理想模型的抽象概括过程;是分析综合、推理论证等方法的内化. “科学思维”主要包括了模型建构、科学推理、科学论证、质疑创新等要素.由此可见,“科学思维”是原有三维目标中“过程与方法”中“方法”维度在物理学科中的传承与发展[1].
以往已有不少教师对液柱移动问题进行分析.姜炜星利用判别式法对气体动态过程进行分析[2],并提出压力的变化才是分析液柱移动的根本这一观点;顾爱芬在姜炜星基础上增加了运动状态变化影响液柱移动的分析[3];华兴恒则是从方法分类的角度,从假设法、超(失)重法、特殊值法等多种方法对液柱移动问题进行归纳[4].前人的论文对液柱移动问题的分析要么只针对一两个子问题,要么以方法分类而缺乏多种方法解决同一道题,因此,本文将围绕温度变化、运动状态变化、试管位置变化及液体增减4种不同的情境,结合不同的物理方法解决液柱移动问题.
1 温度变化导致液柱移动
1.1 横截面积相等的液柱移动分析
【例1】 如图1所示,两个体积不等的容器A和B通过一根水平细管连接,玻璃管中有一段水银柱将两部分气体隔开,此时A气体温度为17 ℃,B气体温度为67 ℃(细管的体积不计),水银柱温度稳定,若两边温度都升高40 ℃,问
(1)水银柱如何移动?
(2)气体A,B初末状态的压强变化量ΔpA和ΔpB是什么关系?

图1 例1题图
分析:本题中,两段封闭的气体由于温度发生变化而导致液柱移动.液柱移动的本源其实是受力状态发生变化.因此,解题的突破口是找出气体A对液柱左侧面的压力变化ΔFA和气体B对液柱右侧面的压力变化ΔFB之间的大小关系.由于温度变化会导致压强、体积均发生变化,因此,需要先假设液柱不动,气体A,B均经历等容过程.然后,运用理想气体状态方程计算出气体A和B升温后的压强变化ΔpA和ΔpB,再乘以面积便可得出ΔFA和ΔFB的关系.本题还可用极限分析法在假设法和反推法的结合下快速解答.但需要注意的是,假设液柱不动的压强变化是在非稳定状态下的,与稳定状态下的压强变化量并不相同.
解析:(1) 解法1,假设液柱不移动,气体A,B均经历等容过程,pA,pB,TA,TB分别是气体A,B的初始状态参量,而ΔpA,ΔpB,ΔTA,ΔTB则是气体A,B状态参量的改变量.
气体A,B的压力比值可由压强公式得出
(1)
根据查理定律,对气体A有
(2)
所以
同理,对B气体有
将ΔpA和ΔpB的表达式代入式(1)中,得
(3)
在该情境下,气体A,B初始时处于平衡状态,所以pA=pB,而液柱左右两侧横截面积相等,则SA=SB,升高温度相同,则ΔTA=ΔTB.所以式(3)为
气体升温,压强均增大,因此压力也均增大.根据牛顿第二定律可推出气体将向右移动.
解法2,假设液柱不移动,气体A,B均经历等容过程.假设气体A,B均缓慢降温至0 K.因为气体B的初温比气体A的高,所以气体A先到达0 K.由理想气体状态方程pV=nRT可知,当T=0 K时,压强也为0 Pa.所以当pA=0时,pB>0,因此液柱向左移动.气体A,B降低温度,液柱会向左移动.升高温度则是降低温度的逆过程,则在升高相同温度的情况下,液柱将向右移动.
(2) 题目(1) 中的ΔpA>ΔpB,ΔFA>ΔFB均是在假设气体做等容变化的条件下获得的,而实际情况气体并非等容.初末状态气体均达到稳定的平衡状态,因此液柱受力平衡,气体A,B初末状态的压强变化量ΔpA和ΔpB相等.
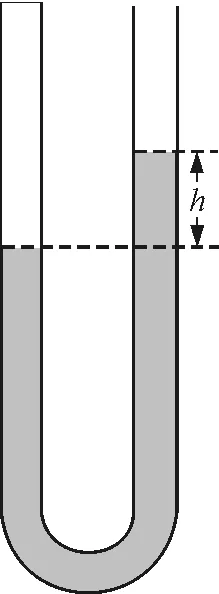
【例2】 如图2所示,粗细均匀的两端封闭的U形管,内装有一段水银柱,两管水银面高度差为H,水银面上封有理想气体,现把U形管浸没在热水中,则管内水银面高度差将如何变化?
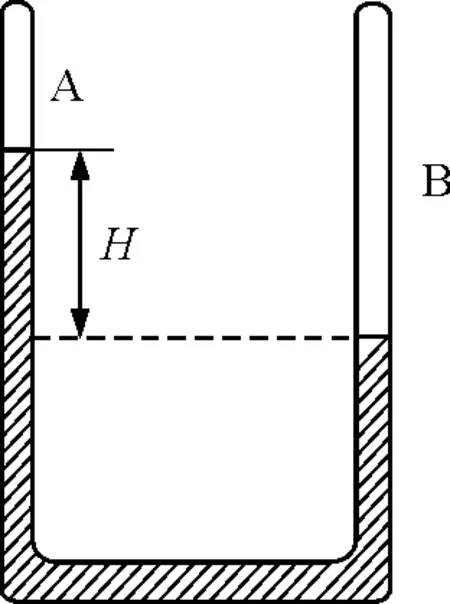
图2 例2题图
分析:本题中,两段封闭的气体由于温度发生变化而改变了自身的压强,左管中高H的水银柱所受到的压力也随之改变,进而使得液柱发生了移动,高度差发生变化.因此本题可以利用例1中的式(3)计算出气体A,B压力变化量的关系,也可以利用极限分析法快速解题.
解析:解法1,假设液柱不发生移动,气体A,B均经历等容过程.将左管中高为H的水银柱作为分析对象,其运动状态的变化来源于上下表面受到的力大小不一致.水银柱的上下表面的横截面积相同,即SA=SB,气体A,B的初始温度和变化温度均相同,即
TA=TBΔTA=ΔTB
则式(3)变为
因为
pA+ρgH=pB
所以
因此左管中液柱将向上移动,右管中向下移动,液面高度差将变大.
解法2,假设液柱不发生移动,气体A,B均经历等容过程.由极限分析法再假设气体A,B均缓慢降温至0 K,由于气体A,B初温相同,因此,两种气体同时达到0 K.根据理想气体状态方程pV=nRT可知,当T=0 K时,压强也为零,因此两种气体压强同时降到零.在这种情况下,由于重力作用左管液柱会向下移动.因此可以反推出随着温度升高,左管液柱会向上移动,液面高度差将变大.
1.2 横截面积不相等的活塞或液柱移动分析
【例3】如图3所示,A,B是两个固定在地面上的气缸,它们的活塞用硬杆连接,两气缸内装有同种气体,温度相同,平衡时体积也相等.若两活塞间的空间为真空,不计一切摩擦阻力,则当两气缸内气体升高相同温度时,活塞向哪一端移动?

图3 例3题图
解析:解法1,先假设活塞不移动,两侧封闭气体均做等容变化.气体A,B初温相同,温度变化量也相同.由于活塞最开始处于受力平衡状态,则
pASA=pBSB
则式(3)变为
所以活塞不移动.
解法2,先假设活塞不移动,两侧封闭气体均做等容变化.由于两种气体初温相同,由极限分析法可知当均降到0 K时,左右两种气体压强为零,活塞不移动.则升高温度时,活塞亦不移动.
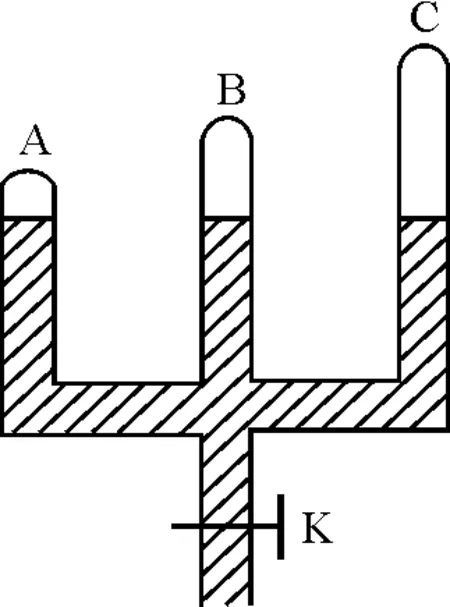
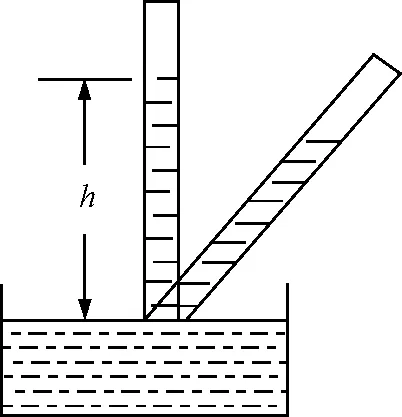
【例4】如图4,为竖直放置的上细下粗的密闭细管,水银柱将气体分隔成A,B两部分,初始温度相同.使A,B升高相同温度达到稳定后,水银柱与原来相比是上升了还是下降了?

图4 例4题图
解析:解法1,对液柱进行受力分析,可知其受到重力、气体A,B对它的支持力和压力以及肩部对它向下的压力.因此在考虑了肩部对液体的力学效果后,A气体实际对液柱作用等效面积应等于液柱下表面面积减去肩部的面积,即S′A=SB.而气体A,B压强关系为pB+ρgH=pA,所以pB 所以液柱向上移动. 解法2,利用极限分析法对气体A,B进行降温分析也可以得到同样的结果. 如图5所示,在玻璃管处于静止或匀速直线运动时,玻璃管中的水银柱受力平衡,气体A,B对水银柱的压力相等,即 FA=FB 又由于水银柱的左右两侧面积相等,则 pB=pA 当水银柱向右加速运动或向左减速运动,即加速度方向向右时.由牛顿第二定律对水银柱进行受力分析,可知 F′A-FB=ma 所以 F′A>FB 即p′A>p′B.所以pA变大,pB变小.对气体A的等温变化过程运用玻意耳定律pV=C可知其体积变小,同理可得气体B体积变大.因此,我们可将该结论对所有因运动状态变化导致液柱移动的问题进行推广:无论水银柱是水平加减速、竖直加减速抑或是旋转运动,均先判断运动的加速度方向,水银柱移动的方向则与加速度方向相反. 图5 玻璃管中水银柱移动问题 【例5】如图6所示,水平放置的两端封闭和粗细均匀的玻璃管中有一段水银柱把气体分为两段,若使该玻璃管随同圆台一起转动,则水银柱如何移动? 解析:由于水银柱的加速度是指向圆心,因此水银柱将沿着半径向外移动. 图6 例5题图 【例6】如图7所示,外界大气压为一个标准大气压,当玻璃管竖直放置时,管内外水银面高度差h=70 cm,若保持温度不变,则当玻璃管绕开口端缓慢转动时,管内水银柱长度将( ) A.变小 B.变大 C.不变 D.无法确定 图7 例6题图 分析:在玻璃管转动的过程中,液柱在试管中可能会上下移动,导致气体的体积发生变化,气体的压强也随之变化.因此,需要假设水银柱在试管中不动,分析气体压强的变化,再由玻意耳定律判断压强变化所造成的对气体体积的影响. 解析:假设水银柱在试管中不动,则随着玻璃管绕开口端缓慢转动,气体的压强由于水银柱竖直高度减小而增大.由玻意耳定律pV=C可知气体的体积将减小,因此水银柱将沿着管上升.而水银柱是否会上升到原来的高度呢?水银柱上升后,密封气体的压强比最开始的大,由外界气体压强与密封气体压强的关系式可以推出水银柱虽然沿着管上升,但比最开始的竖直高度还是要低一些. 【例7】如图8所示,一个上端封闭的玻璃管竖直插入水中,管中水面在管外水面之下,管上某点A和容器上某点B与管内水面等高.如果把管再向上提一些(管口不离开水面),则管内水面相对于A点______,相对于B点______. 图8 例7题图 分析:玻璃管向上提的过程,气体将经历等温下体积和压强均发生变化的过程.因此,可以假设玻璃管中气体体积不变或液柱与玻璃管相对不动作为前提进行分析,再结合玻意耳定律便可探究出气体体积的变化.也可以将管中液柱保持原有高度不变作为前提假设. 解析:解法1,假设液柱与玻璃管相对不动,即管内气体体积不变.在玻璃管上提的过程中,液面与管外水面的高度差减小,则管内气体压强将变小.由玻意耳定律pV=C可知管内气体的体积将变大.因此液柱将向下移动,在A点之下.但最终管内压强比初始压强小,所以液面高度差将变小,管内液柱的上表面在B点之上.所以管内水面相对于A点下降,相对于B点上升. 解法2,假设管中液柱保持原有高度不变,在玻璃管向上提的过程中,气体体积变大.由玻意耳定律pV=C可知气体压强变小.结合内外液面高度差可知管中液柱将向上爬升,但最终需保证气体体积比初始体积大且压强比初始压强小的结果.因此管内水面相对于A点下降,相对于B点上升. 【例8】如图9所示,一定质量的空气被水银封闭在静置于竖直平面的U形玻璃管内,右管上端开口且足够长,右管内水银面比左管内水银面高h,沿管壁向右管内加水银,h将变______. 分析:研究对象锁定为左管中的气体,左管中气体体积的变化会导致水银面高度差发生变化.需要假设左管气体体积不变,探究在此假设前提条件下加水银对气体压强的影响,再利用玻意耳定律分析出气体体积的变化. 图9 例8题图 解析:假设左管气体体积不变,在往右管中加水银的过程中,高度差h将变大.设左管中的气体压强为p1,空气压强为p0,则p1=p0+ρgh,则气体压强变大.由玻意耳定律pV=C可知气体的体积将变小.所以左管中液柱向上爬升.但由于最终结果是左管中气体压强比初始压强大,因此由p1=p0+ρgh可知最终的液面高度差h将变大. 【例9】如图10所示,上端封闭的连通器A,B,C 3管中水银面相平,管中水银上方的空气柱长lA 图10 例9题图 分析:打开阀门后,3管中的水银均会下降.平衡后3管中水银面的高度关系其实是3管中气体的压强关系.因此本题需要寻找一个相同量作为前提假设——平衡后3管液面高度相同. 解析:假设流出水银后3根管中的高度依旧一致,即 ΔVA=ΔVB=ΔVC 假设A管中气体的初始体积和压强分别为VA,pA,流出水银后的体积和压强分别为V′A,p′A,由玻意耳定律可知 V′Ap′A=VApA 得 因为初始气体体积 VA pA=pB=pC ΔVA=ΔVB=ΔVC 所以流出水银后气体压强为p′A 因此,在假设流出水银后3根管高度保持一致的条件下,液体将流向气体压强较低的地方,因此最终水银面的高度关系为lA>lB>lC. 课程标准指导着高考命题的走向.在新课程标准的指导下,高考题更应该注重过程分析与科学思维的考查.热力学中液柱移动问题由于其本身所蕴含的丰富的科学思维方法,如假设法、控制变量法、反推法、模型法、极限分析法等,使学生在解题过程中往往需要经历完整的模型建构——由液柱移动的情境建立起受力状态变化的物理模型,科学推理——在提出不变量的假设后围绕理想气体状态方程探讨p,V和T3个物理量之间的联系,科学论证——多种解法得出相同的结论之后对自己的思维过程进行科学论证,因此这类题目在新高考中更能彰显其价值.2 运动状态变化导致水银柱移动问题

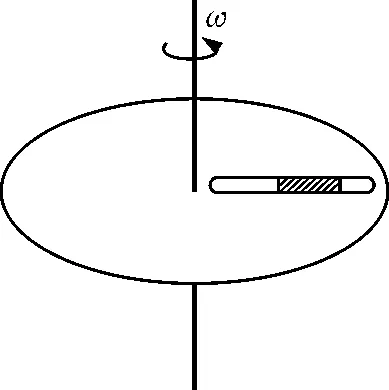
3 试管位置变化导致的液柱移动问题

4 试管液体增减引发的液柱移动