基于网络拓扑结构的重要节点发现算法
2019-08-19邓晓懿
邓晓懿, 杨 阳, 金 淳
(1.华侨大学 工商管理学院,福建 泉州 362021; 2.大连理工大学 系统工程研究所,辽宁 大连 116024)
0 引言
复杂网络由大量节点组成,其中重要节点是少数能对整个网络的结构及功能产生深层次影响的特殊节点。在网络安全、信息传播、疾病防控、犯罪预防、交通及电力传输等领域中,少数重要节点的影响可以快速地波及到网络中大部分节点状态。例如,在internet中,只需攻击其中5%度大于5的网络节点就能阻断因特网的连通性[1];美国俄亥俄州克利夫兰市的电力传输故障导致了整个北美电力网络瘫痪;在全球经济网络中,控制着40%财富的147家跨国公司数量不到全球公司总量的1%[2];在SNS网站(Weibo,Twitter或Facebook)上,少数具有较强影响力的用户所发的信息会很快就会传遍整个网络。因此,重要节点对网络的结构和功能有着巨大影响, 如何发现复杂网络中的重要节点、并度量其重要性具有重大理论意义和实际应用价值[3,4]。
在复杂网络中,节点的重要性依赖于网络拓扑结构,其常见度量指标有度中心性(Degree Centrality, DC)[5]、介数中心性(Betweenness Centrality, BC)[6]、接近中心性(Closeness Centrality, CC)[7]、特征向量中心性(Eigenvector Centrality, EC)[8]等。相对其他方法,EC不但蕴含着节点的特征信息(如重要性、声望以及地位等),同时更强调节点所处的周围环境,认为节点重要性不但取决于其邻居节点的数量,还取决于其邻居节点的重要性[9]。换句话说,节点的EC值即为其所有邻居的EC值之和,节点可通过连接其他重要节点的方式来提升自身重要性,EC值较高的节点要么和大量一般节点相连,要么和少量具有较高EC值的节点相连。因此,EC更适用于描述节点的长期或者全局影响力,例如在传染病传播网络中,如果节点EC值越大,那么该节点很可能距离传染源很近,或为感染源之一,是需要重点关注或控制的关键性节点。
传统复杂网络重要节点发现算法可分为局部发现和全局发现,局部发现算法仅考虑节点自身属性和其邻居信息,而全局发现算法侧重衡量节点在网络的全局信息。EC算法[8]则是全局发现算法中的一种代表性算法。由于EC算法思路简单,复杂度较低,在很多领域中受到极大关注[9]。但是,EC算法将所有节点归为一个社区,并未考虑节点局部所在社区的聚集程度,也未利用社区的结构特征度量节点的重要性,不能充分满足重要节点的发现要求。针对EC算法的不足,本文提出了可达中心性算法(Accessibility Centrality, AC)。该方法基于网络拓扑结构来度量节点之间的影响力,依靠邻接矩阵传递控制路径长度,强化了节点的结构性特征;此外,该方法同时考虑了节点的局部影响力和全局影响力,可弥补EC算法仅基于节点全局影响力进行计算的不足,可进一步提高重要节点发现的效率和准确性。
1 类EC算法分析
EC算法是基于特征向量的节点发现中的核心代表算法[10],是评价复杂网络节点影响力的重要算法之一。EC算法、EC改进算法以及变体通常称为类EC算法,本节针对类EC算法进行概述分析。
1.1 EC算法概述
EC算法认为网络中的每个节点都有一个相对状态值,节点的相对状态值受到该节点的邻居相对状态值的正向反馈,在不断反馈迭代过程中,节点相对状态值标准化后达到稳态,此时的稳态值就是节点的EC值。
假设G=(V,E)为一个无向无权网络,A=(Aij)为其邻接矩阵,即:
(1)
根据EC算法定义,设S=[S1,S2,…,SN]T为节点的相对状态,uS=[uS1,uS2,…uSN]T为节点相对状态标准化值,S0=[1,1,…1]T为节点的初始状态值。迭代过程如下:
Step1节点第一阶段状态值等于初始阶段节点邻居状态值之和的倍数,即S1=AS0/λ1;
Step2节点第二阶段状态值等于第一阶段节点邻居状态值之和的倍数,即S2=AS1/λ1;
……
StepN节点第N阶段状态值等于第N-1阶段节点邻居状态值之和的倍数,即SN=ASN-1/λ1。其中,λ1为一个比例常数,多次迭代直到uSN=uSN-1为止,uSN等于EC向量。从上述过程可看出,EC算法更适合评价节点长期影响力。
1.2 相关研究概述
在EC算法改进方面,Redner[11]将EC算法应用拓展到加权EC算法,并将加权EC应用到引文网络的搜索结果排序。Ilya[12]提出主分量中心性算法,利用邻接矩阵的前p个特征向量来计算节点的中心性,解决了EC算法认为重要节点集中于一个社团的缺陷。李静茹等[13]提出基于链接强度矩阵的加权中心性度量法,将PCC应用于加权社交网络,在传播效率、鲁棒性、容错性等方面比加权EC算法更优。Martin等[14]利用非回溯矩阵解决了EC算法局部转移问题,并适用于大型复杂多社区结构网络。另一面,对于提高EC算法效率,Poulin等[15]提出在EC算法邻居节点每次正向反馈时加入节点自身的状态值,提高了收敛速度。Kohlschütter等[16]提出并行算法计算邻接矩阵的特征向量和特征值,提高了运行速度。
在EC算法变体方面,网页排序领域的PageRank算法[17]通过模拟用户上网浏览网页过程,沿着访问路径将节点状态值平均分配给其他页面,使节点网页得到一个全局的重要性排序,但当网络不连通时,节点排序结果不唯一。基于PageRank算法,LeaderRank算法[18]在原网络中加入一个背景节点(Ground Node),并将这个节点和网络中所有节点相连,保证了网页的强连通性,更能识别网络中有影响力的节点。Li等[19]则认为入度较大的节点在遍历过程中被访问的概率应该更高,利用背景节点和其他所有节点的链接赋予不同权重提升了LeaderRank算法效果。上述研究都将节点视为同质节点,而Kleinberg[20]则认为节点重要性不应该依赖于单一指标,应采用权威值和枢纽值两个不同指标对网络节点进行排序,每个指标同样依赖邻居指标的贡献。Benzi等[21]将有向网络映射成无向二分网络,运用矩阵函数计算节点权威值和枢纽值。
上述研究针对EC算法的不足,做了相应改进或优化,在一定程度上提高了EC算法的效率,并扩大了其应用范围。但是,其中大部分研究都是将邻居作为传播路径,应用邻居的正向反馈进行节点影响力评估,过于注重节点参数的收敛性,忽略了网络拓扑结构对节点影响力的影响,同时也未讨论反馈不同阶段中节点影响力变化情况。
2 基于网络拓扑结构的可达中心性算法
2.1 算法核心思想
在现实社交网络中,如果节点A和B是朋友,那么节点A的另一个朋友节点C也可能是节点B的朋友,由此形成一个三角形关系结构。此时,节点的结构特性可用集聚系数(Clustering Coefficient)表示,若节点邻居之间三角形关系结构的边越多,节点的集聚系数越大。EC算法则可看作信息在网络中进行无损失传播的模拟过程,并依靠邻居节点重要度测量节点影响力。事实上,在可达的情况下,节点可以对其他任意节点贡献重要度。此外,节点所在社区的结构越密集,节点信息的传播路径越多,其影响力越大;同时,传播过程中会出现信息丢失,信息丢失程度与路径长度成正比。
本文提出基于网络拓扑结构的可达中心性算法(Accessibility Centrality, AC),从节点结构特征和网络的传播特性两个方面对EC算法进行改进:首先,根据网络的节点结构特征,利用邻接矩阵计算网络中不同路径长度下的节点间影响力;然后,根据节点间影响力得到不同路径长度下的节点影响力;最后,根据网络的信息传播特性得到最终节点的影响评价指标AC值。AC算法框架如图1所示。
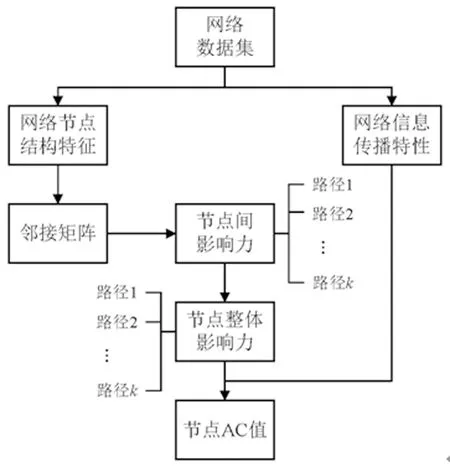
图1 AC算法框架
设无向无权网络G=(V,E),节点数N,邻接矩阵为A=A(i,j),G中节点间存在影响力F(i,j)。若节点i能影响节点j,从网络拓扑结构上就存在着连接节点i到节点j的路径。相同路径长度下节点i到达节点j的路径数越多,节点i对节点j的影响力越大。为研究不同路径长度下节点影响力变化情况,本文在接下来的章节分别对不同路径长度下的节点间影响力和节点整体影响力进行定义并详细阐述。
2.2 节点间影响力
为便于理解节点间影响力,本节以一个小型无向网络G为例进行阐述。图2所示的网络可看作由两个大小相等的社区所构成的网络,具有10个节点和13条边。

图2 小型无向网络G示例
在图2中,网络G中节点i1和i6都与4个节点相连,由于i6所在社团结构更为紧密,显然i6对i5的影响力F(6,5)大于i1对i5的影响力F(1,5)。当路径长度为1时,i1和i6到达i5的路径分别是1→5和6→5;当路径为2时,i1和i6无法到达i5;当路径长度为3时,i1和i6到达i5的路径数量仍旧相同;当路径长度为4时,i1无法到达i5,但i6可以通过6→7→10→6→5和6→9→10→6→5两条不同路径到达i5,说明随着路径长度增加,i6对i5的影响力优势不断增加。因此,F(6,5)的大小不仅与i6和i5的直接到达路径数量直接相关,而且与不同路径长度下的间接到达路径数量有关。
定义1k步路径节点间影响力Fk(i,j):节点i对节点j的k步路径影响力等于节点i在长度为k的连接路径下到达节点j所遍历的节点数量,如公式(2)表示。

(2)
其中,节点i对j的1步路径节点间影响力F1(i,j)=A(i,j),对于节点i对j的k步路径节点间影响力Fk(i,j),l为网络中任意节点,当Fk-1(i,l)和A(l,j)都不为0时,表示i可继续通过节点l对j施加影响力,Fk(i,j)在Fk-1(i,l)的基础上增加了一个遍历节点l。
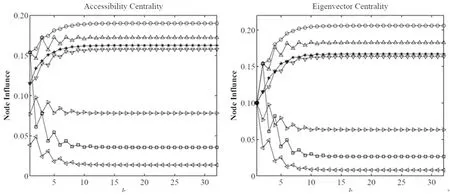
图3 节点uf k值和EC值变化趋势
由此可见,Fk(i,j)不仅考虑了两两节点间的可达路径数量,同时还累计了路径上的节点个数,可使处于社区结构相对紧密的节点的影响力更大,而处于社区结构相对稀疏的节点的影响力更小,最终可使节点影响力的收敛速度更快,具体详见图3。
2.3 节点整体影响力
定义2k步路径节点整体影响力fk(i):节点i的k步路径整体影响力等于该节点到所有节点(包含其自身)的k步路径节点间影响力Fk(i,j)之和,公式表示如下。
(3)
以图2中网络G为例,G中10个节点在1步~6步路径长度下节点影响力如表1所示。由表1可知,节点2、3、4以及节点7、9的影响力变化一致,这是由于节点7、9和节点2、3、4分别处于对称位置,使得这些节点在不同路径长度下到达其他节点的遍历路径长度相同。

表1 节点k步路径节点影响力
为便于比较不同路径下节点整体影响力,本文以网络G中节点1、2、5、6、7、8、10为例进行说明。节点fk(i)值和EC(i)变化趋势如图3所示,其中,fk(i)按照公式(4)做标准化处理。
(4)
由图3可知,节点7、8的ufk差值显然大于它们的EC差值,其他节点之间的ufk差值也比EC差值更为明显。对于节点1而言,尽管其邻居较多,但由于其所在社区结构相对稀疏,造成其ufk值迅速下降,且其在3步路径长度下的ufk值小于节点5的ufk值,波动幅度小于EC算法,说明AC算法的收敛速度比EC算法更快。
2.4 节点影响力评价指标
在得到节点整体影响力之后,再对每个节点的长期影响力进行评估。在计算节点的长期影响力时,为了考虑节点的全局影响力,EC算法将节点影响力的最终稳定值作为节点的长期影响力评价指标。为了考虑节点在所有传播路径下的全局影响力,本文认为节点影响力评价指标和节点的前k步路径节点整体影响力都有一定的比例关系。此外,相关研究[3]表明:节点影响力的传播路径上存在噪音干扰,传播的影响力大小与路径长度成反比。
定义3节点影响力评价指标AC(i):节点的影响力评价指标等于标准化的全体k步路径节点整体影响力ufk与路径长度k的比值之和,计算公式如下所示。
(5)
其中,K为任意两节点之间不含闭环的最大可达路径长度。在G中,当K=15时,根据公式(5)得到每个节点的AC值;同时,根据EC算法得到每个节点的全局影响力,结果如表2所示。

表2 AC算法和EC算法的节点影响力计算结果
从表2可以看出,根据AC算法和EC算法计算出的节点影响力排序所得到的两组节点序列完全一致,进而证明了AC算法具有与EC算法相同的节点影响力排序有效性。
大量实验证明,任意两节点间不含闭环的最大可达路径长度K的大小与网络的拓扑结构和传染概率有关,当传染概率较大时,K通常等于网络中任意两个节点间最短路径中的最大值(即网络直径),此时可得到节点影响力的最优评价指标,具体详见4.2节的K值分析。由于现实世界的网络具有小世界特性,网络的K值通常较小,可降低AC算法的计算复杂度。
3 实验设计与结果分析
为验证AC算法的有效性以及其在不同集聚度网络上的性能,本文分别采用Email、Ariport等四种真实网络数据,以及Holme-Kim(HK)聚类系数可变无标度网络[22],并选取EC算法等四种主流重要节点发现算法进行对比分析。实验运行环境为CPU Intel E5-4650 2.7GHz CPU, 32GB内存,Window Server 2008操作系统,Matlab R2014b。
3.1 实验设计
3.1.1 实验数据
(1)真实网络数据
本文使用四个真实的无向基准网络数据对比验证AC算法的有效性,四个真实网络包含文本网络Word、社交网络Email、交通运输网络Airport以及生物网络Protein[3],四个网络的特征信息如表3所示。
在表3中,最佳感染概率[23]β0=

表3 基准网络特征信息
(2)人工网络数据
HK网络模型具有小世界、高聚类、无标度特性,非常接近现实中的社会网络和生物网络,可用于分析网络聚类系数对AC算法性能的影响[24]。HK模型的生成由一系列参数控制:N代表节点数量,m为每一个新节点随机连接边的数量,p表示新节点随机连接一条边后再连接一条边可构成三角形的概率,p越大,网络的平均集聚系数越大。本文取N=500,m=3,p∈[0,0.9]且以步长0.1递增,生成N0至N9共10个网络。
3.1.2传染病传播模型
SIR和SI模型是复杂网络中用于测试节点传播能力的经典模型[9]。SIR模型中,节点可能处于三个状态:易感者(Susceptible State, SS),感染者(Infected State, IS)和恢复者(Recovered State, RS),而SI模型中节点只可能处于SS和IS两种状态中的一种。
在仿真初始时刻,待测节点i为IS节点,其他节点为SS节点,IS节点以传染概率β将其的SS邻居节点转换为IS节点。在SIR中,IS节点能以恢复率μ转换成RS节点,RS节点不再转换为IS节点。若在仿真时间(timespace)未结束前,系统中不存在SS节点,仿真过程结束。节点i的传播影响力如公式(6)所示。
(6)
其中,T表示最大重复仿真次数,ki(t)等于节点i在第t次仿真时的影响力传播值。由上式可得节点的影响力序列S=[S1,S2,…,SN]。
3.1.3 对比算法及评估函数
为测试AC算法的性能,本文引入其他四种代表性的重要节点发现算法进行比较,分别是度中心性算法 (Degree Centrality, DC)[5],介数中心性算法(Betweenness Centrality,BC)[6],EC算法[8]和LeaderRank算法[18]。
为评估每个算法得到的节点影响力序列是否与模拟的传染病模型得到的节点传播能力序列一致,本文利用Kendall’s Tau系数[24]作为评价指标。该系数通过比较两段序列:D(例如节点度序列D=[D1,D2,…,DN])和S序列的一致程度,来评估节点传播能力。如果Di>Dj且Si>Sj,或者Di (7) 其中,τ值越大,两列序列的一致程度越高。当τ=1时,两列数列完全一致;当τ=-1时,两列数列完全不同。 为确定网络中K的取值,本文以人工网络N0和N9为研究对象。其中,N0网络直径为7,p=0,K∈[1,10];N9网络直径为8,p=0.9,K∈[1,11]。将该实验结果与SIR模型上的实验结果进行对比,SIR模型参数timespace=5,β={0.04,0.06,0.08},μ=0.05,T=1000。实验结果分别如图4和图5所示。 图4 K取值分析结果 图4结果显示了参数K对节点影响力评估指标AC值准确性影响:τ值随着K值的增加呈现先增加后降低的趋势,不同传染概率下均表现一致。随着传染概率的升高,τ值的增长逐渐变缓。当β分别等于0.06和0.08时,N0中K=7、N9中K=8时τ值分别达到最优。当β=0.04时,可适当降低K的取值以可达到最优效果。 图5 不同集聚系数条件下AC指标准确性变化 图5则显示了不同集聚系数对节点AC值准确性的影响:随着p值的增加,τ值总体呈下降趋势,但下降幅度较小。该结果表明AC算法能够更准确地定位集聚系数较低的网络,找出其中隐含的集聚效应。相对的,对于平均集聚系数较高的网络,AC算法的效果相差不大。 为保证节点的传播能力是有限的,本文在实验中将传染概率β设置为相对较小的值,β∈[0.01,0.1],并以步长0.01递增。SIR、SI模型参数μ=0.05,T=1000。AC算法中K值分别对应各网络的直径。 3.3.1 AC算法有效性分析 为评估AC算法对节点影响力的有效性,本文分别在SIR和SI仿真环境中对比AC与其他四种算法,实验对比结果分别如图6和图7所示。 由图6可知,在Airport和Protein网络中,AC算法的性能完全优于其他四类算法;在Word网络中,AC算法在β的可变范围优于EC和DC算法,且当β>0.02时,AC算法优于DC和LR算法。在Email网络中,AC算法在β的可变范围内优于EC、LR和DC算法,当β>0.02时,AC算法比其他四种算法更有效。从总体上来看,当β>β0时,AC算法的τ值随着β增加而增加,这是因为待测节点的邻居数量以及邻居节点被影响的概率增加,导致其他节点的被影响概率也随之增加,使得节点影响力的传播范围变大。当β<<β0时,节点影响力的传播仅发生在待测节点周围,度越大的节点可影响节点数量越多。此时,基于局部发现的DC算法的τ值较大,优于基于全局影响力节点发现的EC算法。但随着β的逐渐增加,DC算法的τ值转而降低,很快劣于基于节点长期影响力的EC和AC算法。在相同条件下,AC算法可以在β<<β0时就获到比EC更优的τ值,说明AC算法在较低的传染概率条件下也能得到有效的节点影响力评估。此外,AC和EC算法的τ值曲线在Airport网络中的差异最小,而且Airport网络的平均集聚系数远高于其他三个网络,进一步证明了AC算法在低集聚系数网络上的有效性要优于高集聚系数网络。从总体上看,ACfigureEC算法。 图6 五类算法节点影响力与SIR模型模拟结果对比τ值变化趋势 图7 五类算法节点影响力与SI模型模拟结果对比τ值变化趋势 通过观察图7的4个子图,可发现在SI仿真环境下,AC及其他四种算法的对比效果与图6中的效果基本一致:在Word和Email数据上,当β>0.02时,AC算法优于其他四类算法;在Airport和Protein数据集上,AC算法则完全优于其他四类算法。同时,当β>β0时,AC算法的τ值随着β增加而增加;当β<<β0时,相对于EC算法,AC算法可更有效地评估网络节点的影响力,说明AC算法更适用于分析低集聚系数网络。可以说,在SI仿真环境下,AC算法在四个网络上的节点评估能力均优于EC算法。 五种算法在β∈[0.01,0.1]上的平均τ值<τ>分别如表4和表5所示。从表4和表5可以看出,AC算法在四个网络上与SIR、SI模拟结果对比均能得到最优<τ>,说明基于网络拓扑结构的AC算法在所有网络中评价节点重要性时具有最佳的有效性,进一步证实了网络拓扑结构在发现重要节点过程的重要性。换句话说,结合网络拓扑结构分析重要节点对网络结构稳定性和功能的影响会更加有效、更有意义。 表4 五个中心性算法与SIR模型模拟序列对比τ平均值 表5 五个中心性算法与SI模型模拟序列对比τ平均值 3.3.2 AC算法准确性分析 图8 五类算法在前top-N节点影响力评估τ值变化趋势 由图8可知,AC算法在Word、Email和Protein网络中都具有最优τ值。在Airport网络中,当top-N∈[100,300]时,AC算法的精度比其他算法更高;当top-N∈(300,700]时,AC算法和EC算法的精度在总体上保持一致;当top-N∈(700,1000]时,AC算法精度又优于其他四种算法。从整体上看,AC算法相比其他四类算法能够更准确地发现网络中最有影响力的节点或者重要节点。由于现实中的大型网络有相当一部分节点通过网络中的重要节点或者最有影响力的节点与网络中的其他部分连通,通过AC算法准确地发现该类节点,并对其采取有效控制措施,可进而有效控制整个网络。例如,如果能在社交网络中有效控制其中的关键重要节点(最有影响力的用户),就能在最大程度上阻断信息(如谣言等)的传播路径,进而控制舆论。 本文在深入研究EC算法的基础上,分析了网络拓扑结构和信息传播特性对节点重要性的影响,提出基于网络拓扑结构的可达中心性算法。该算法不但考虑了节点所有的传播路径,可计算节点的全局影响力,还能根据不同路径长度下节点的传播影响力计算出节点的局部影响力。然后,本文分析了网络节点集聚系数对AC算法的影响,证明AC算法在集聚系数较低网络上的准确性较高。最后,通过模拟SIR和SI两种传染病模型在四个真实网络中的传播过程,对比分析了AC算法的有效性和准确性。实验结果表明,与LeaderRank等四类算法相比, AC算法在不同传染概率下所得到节点影响力序列更接近与SIR和SI模型所得到的节点影响力序列,说明AC算法的准确性比其他四类算法更高,可在不同拓扑结构的网络中更有效地评估节点的影响力、准确发现重要节点,同时更适用于分析聚集系数较低的网络。 本文通过计算节点在不同路径长度下到达其他节点的节点间影响力计算节点的全局影响力,进而获得节点的影响力评价指标,以探索无向网络中的重要节点挖掘方法。对于有向网络而言,其节点影响其他节点的路径包括传入路径和传出路径,如何分配不同路径长度下影响力传入及传出的权重,进而得到最优评价指标尚有待于进一步研究和解决。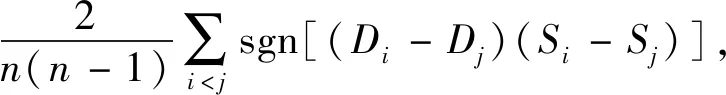

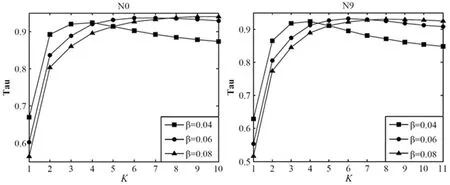
3.2 K取值分析和HK模型仿真结果分析
3.3 实验结果及分析


4 结论
