基于输出约束的电液伺服系统非线性方法研究
2019-08-19
(1. 电子科技大学航空航天学院, 四川成都 611731; 2. 电子科技大学机械与电气工程学院, 四川成都 611731)
引言
电液伺服系统是液压伺服系统的分支,因电气控制灵活而得到广泛的应用。电液伺服系统通过使用电液伺服阀,将小功率的电信号转换为大功率的液压动力,具有控制精度高、响应速度快、输出功率大、信号处理灵活、易于实现各种参量的反馈等优点,从而实现了一些重型机械设备的伺服控制。
电液伺服系统是非线性系统中严格的反馈模型,非线性系统的控制问题中一个非常重要的问题即输出约束的有界性,即在保证闭环系统中的闭环信号有界的同时保证输出约束不被侵犯。这主要是因为实际情况下的系统设计的保守型很大,在针对电液伺服系统的实际操作中,破环约束可能会导致性能的降低,甚至会损坏硬件,危及系统,所以约束控制就成为实际控制理论的重点研究领域之一,也是用于提高系统稳定性的重要因素之一。控制领域中已有的研究已经进行了大量的关于约束问题的探讨,还提出了一种基于不变集的概念以解决约束问题,然而,当且仅当初始状态被约束在一个不变集的情况下,约束条件才能够被满足[1-2]。模型预测控制也得到了很好的研究,主要是需要在一个合理的时间段内在线求解最优控制算法,用于解决状态和控制变量的强制约束[3]。19世纪俄国数学家LYAPUNOV提出Lyapunov稳定理论之后,这种方法就成为了非线性控制的一个重要的方法[4-5],并在以后的研究过程中取得了一系列的研究成果,后来又有学者提出障碍李亚普诺夫函数。障碍函数是一类连续函数,其值随着自变量在有界范围内变化而趋于无限。多种控制方法先后应用于非线性系统的控制中,如自适应控制[6-9]、滑模控制[10]、反步递推控制[11-12]、鲁棒H∞控制[13]等。研究[14-15]也有效证明了在处理对称和不对称甚至是带有不确定参数的一类非线性系统的输出约束问题上,障碍李雅普诺夫函数确实是一种非常可观的度量函数。严格反馈非线性系统在设计控制器的时候通常和反步控制相结合,反步控制为控制器的设计提供了一种方法。
本研究针对于电液伺服系统的输出约束问题,提出了将反步控制和障碍李雅普诺夫函数相结合的控制方法来设计控制律。障碍李雅普诺夫函数在解决非线性系统中的状态和输出约束上有较为突出的贡献,当状态或者输出约束达到一定的约束限制的时候,整个函数就会趋于无穷大,这就确保了在系统运动过程中约束限制被破坏的可能[16]。本研究通过构造关于状态变量和期望值误差的方法,得到了确保系统能够渐进稳定跟踪期望的3个控制律,并保证系统在李雅普诺夫议意义下是稳定的。最后将所推导的控制方法应用在由电液伺服系统驱动的二自由度机械臂平台上,得到了理想的实验数据。
1 电液伺服系统的数学模型
根据电液伺服系统的流量方程、动力学方程、流量-压力方程构建三阶数学模型,图1是电液伺服系统的示意图。
液压阀的负载流量Qa满足如下:
(1)
液压缸流量-压力连续方程表示为:
(2)
机械动力学方程表示为:
(3)

图1 电液伺服系统结构图
令系统的状态变量为:
(4)
控制变量为u,输出变量为y=x1,则电液伺服系统的非线性状态空间模型如下:
(5)
其中,x=[x1,x2,x3]T为状态向量。
假设所有的状态和参数都是可测的,并对上式进行简化,有:

(6)
(7)
所以状态方程就可以化简成为:
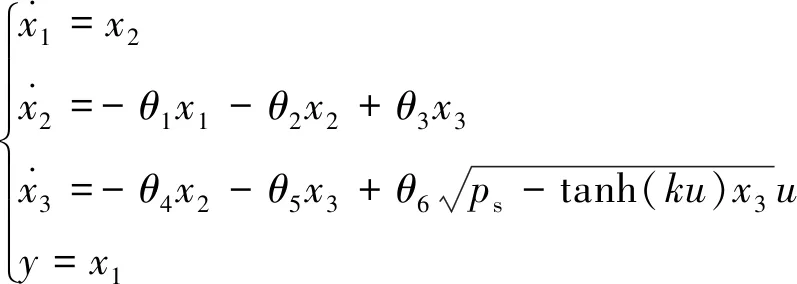
(8)
至此,电液伺服系统的数学模型构建完成。
2 电液伺服系统的控制器的设计
本研究中令zi表示状态/输出跟踪误差,x1d为期望输出,αi为每一步要设计的虚拟控制器(i=1, 2, 3)。
第1步:令z1=x1-x1d,z2=x2-α1这里的z1,z2,α1分别为第一步的状态误差、第二步的状态误差、第一步要设计的稳定的虚拟控制函数。
选择正定且对称的障碍李雅普诺夫函数:
(9)
又可以推得:
(10)
则V1对时间的导数:
(11)
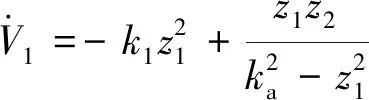
(12)
第2步:z3=x3-α2,z2对时间进行求导有:
(13)
选择第2步的能量函数,即障碍李雅普诺夫函数再加上一个二次有:
(14)
V2对时间的导数为:
(15)
于是选择控制器α2为:
(16)
(17)
第3步:z3对时间进行求导:
(18)
选择最后一步的能量函数,即在第二步的基础上添加一个关于误差的二次函数:
(19)
对时间进行求导,可以得出如下结论:
(20)
选择控制器u为:
(21)
(22)

3 模拟与仿真
仿真过程中为各个参数选定相应的值,令期望输出为正选函数。参数设置为k1为1000,k2为100,k3为100,期望输入为0.05 sin(0.5 πt),Cd为0.62,ps为4 MPa,Vt为1.73×10-5m3,Ksv为7.9×10-4m/V,Ctl为2.5×10-11m2/(s·Pa),m1为 1.771 kg,m2为 0.739 kg,mf为1 kg,m1f为 3.511 kg,m2f为1.739 kg,w为0.024 m,Ap为2.01 cm2,βe=2.2×109Pa。参数选定以后,就可以进行仿真了,仿真图如图2所示。

图2 实际输出x1和状态误差的变化曲线
由图3可见误差已经被控制在6e-4以内,故能够在保持很小的误差范围内跟踪期望的输出。
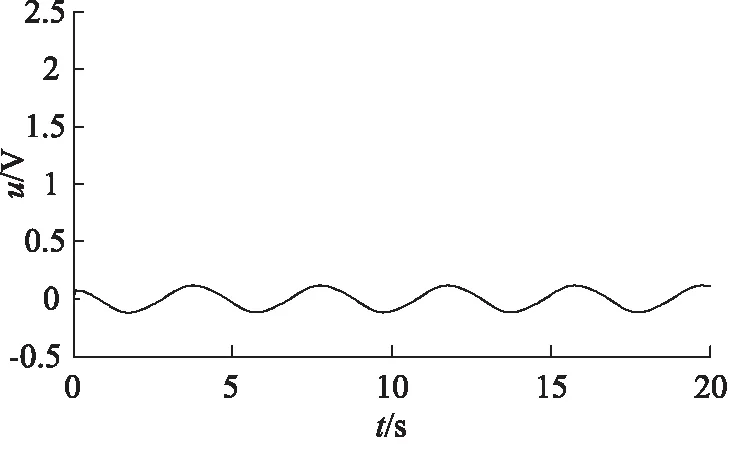
图3 输入u的仿真图
输入u的仿真图也就是本研究中构造的最终的控制器,由图可见输入平稳且稳定,图4和图5是反步控制器中给出的2个虚拟控制量,其变化趋势与实际输出位移和控制量的变化趋势大致相同。
4 结论
本研究针对于电液伺服系统的输出约束问题提出了将反步控制和障碍李雅普诺夫函数相结合的控制方法来设计控制律。通过构造关于状态变量和期望值误差的方法, 得到了确保系统能够渐进稳定跟踪期望的三个控制律,并保证系统在李雅普诺夫议意义下是稳定的。最后,将所推导的控制方法应用在由电液伺服系统驱动的二自由度机械臂平台上,得到了理想的实验数据。

图4 虚拟控制量α1的变化曲线

图5 虚拟控制量α2的变化曲线
