模态识别的Bayesian TDD-FFT法及其应用
2019-08-19徐洪俊张其林
吴 杰, 徐洪俊, 张其林
(同济大学 土木工程学院,上海 200092)
不确定度是评价测量结果质量高低的重要指标。随着科学技术和生产的发展,不确定度分析受到越来越高的重视[1]。但在土木工程中,大部分的模态参数识别方法没有考虑识别结果的不确定度问题。Yuen等[2-3]提出了贝叶斯快速傅里叶变换(Bayesian Fast Fourier Transform,Bayesian FFT)方法,通过对原始时域数据进行变换,识别结构的模态特性并求解参数的不确定性。但该方法识别过程存在以下三个问题:①由于后验的概率密度函数(Probability Density Function, PDF)是模态参数的非线性函数,因此模态参数的最佳估计(Most Probable Value, MPV)需要求解一个多维的数值优化问题,计算过程复杂;②Hessian矩阵需要通过有限差分法来确定,导致计算效率低下;③由于模态参数的数量随着测试自由度数量的增加而增加,目标函数的求解涉及到一个病态矩阵的求逆问题。这些问题的存在严重制约了该方法的应用。
Au[4]针对选定的某一共振频率带的单个模态,提出了快速贝叶斯FFT(Fast Bayesian FFT)方法,该方法针对某一共振频率带的单个模态,不需要考虑所计算的自由度数量,模态参数的最佳估计可通过一个四维的数值优化问题来确定,而且Hessian矩阵可以通过对数似然函数关于模态参数的二阶导数快速准确地计算。
Fast Bayesian FFT方法虽然解决了模态参数的MPV和Hessian病态矩阵的求解问题,但并没有进一步对模态参数的后验概率分布进行探讨[5-9]。鉴于此,本文首先基于贝叶斯理论和结构响应概率模型,提出了一种将多测点多自由度信号转换成单测点单自由度信号的Bayesian TDD (Time Domain Decomposition)方法。然后,对单测点单自由度响应下的贝叶斯FFT(Bayesian FFT)方法进行了推导,并利用蒙特卡洛抽样分析得出各个参数的后验概率分布、模态参数MPV和不确定性评估,从而避免了Hessian矩阵的求解运算。最后,提出Bayesian TDD-FFT方法,并利用该方法对上海中心大厦实测数据进行分析,探讨了评估模态参数的后验概率分布及联合分布问题,同时将识别参数结果与Fast Bayesian FFT方法进行了对比分析。
1 理论推导
1.1 Bayesian TDD方法
对于线性结构,一般假设输入为平稳的零均值的Gauss过程,则结构的输出为0均值平稳Gauss过程,即:
Xn×1~N(0,C)
(1)
式中:C为Xn×1响应输出的协方差矩阵。
根据多维高斯分布性质[10], 对于n维的高斯分布Xn×1~N(0,C),必存在正交阵Φn×n,使得:
X~N(0,ΦΛΦT)
(2)
Yn×1=ΦTX~N(0,Λ),其中Λ=diag(λi)
(3)
即Y的各个变量独立。令θ={C},P(θ)为病态的均匀分布:P(θ)=1,满足
P(θ|X)∝P(X|θ)P(θ)
(4)
(5)

(6)
将P(X|θ)写成对数形式,则有:
P(X|θ)=exp[-f(θ)]
(7)
其中,
(8)
由于ΦTCΦ=Λ,Λ=diag(λi),则:
(9)
(10)
要使得P(θ|X)取得MPV值,需f(λ1,…,λi,…,λn)取最小值,则:
(11)
(12)

(13)

在实际结构中,往往只关心所测结构的前k阶振型,测点的维数n>k,由振型叠加原理可得结构的振动响应为:
(14)

1.2 单测点单自由度的Bayesian FFT
对于单测点单自由度振动响应,Bayesian FFT理论如下:
Yk=Fk+iGk=
(15)

考虑到采样通道的电压偏置和傅里叶变换的共轭等原因,仅k=1,2,…,Nq(Nq=int[N/2]+1)所对应的FFT数据被应用于结构的模态参数识别,其所对应的频率值为fk=(k-1)/NΔt。
有关模态参数θ的后验概率密度函数P(θ|{Zk})正比于似然函数P({Zk}|θ):
P(θ|{Zk})∝P({Zk}|θ)=
(16)
式中:Zk=[FkGk]T∈R2,k=1,2,3,…,Nq;Ck为矩阵Zk的协方差矩阵,其表达式为:
(17)
式中:σ2为预测误差的功率谱密度;I2为2阶单位矩阵;Hk为模态响应自功率谱,表达式为:
(18)
(19)
式中:βk=f/fk为频率比,f和ζ分别是单阶模态信号特征频率和阻尼比;S是单阶模态响应的自功率谱。式(17)可写成:
Ck=[(SDk+σ2)/2]I2
(20)
detCk=2-2(SDk+σ2)2
(21)
若将后验的PDF进一步写成关于对数似然函数L(θ)的表达式,则有:
P(θ|{Zk})∝exp[-L(θ)]
(22)
式中:
(23)
将Ck和Zk代入式(23),则有:
L(θ)=-(Nq-1)ln 2+
(24)

(25)
f、ζ、S和σ2的MPV值可通过对式(25)的无约束优化直接求得。求得的f、ζ、S和σ2的MPV值后,利用蒙特卡罗方法对式(22)进行采样分析,得到f、ζ、S和σ2的后验概率分布,进行不确定度分析。
2 计算流程
上文提出的Bayesian TDD-FFT方法的计算流程见图1所示。

图1 Bayesian TDD-FFT方法计算流程图
3 数值验证
3.1 基本参数
本节通过数值模拟对Bayesian TDD-FFT模态参数识别方法进行验证。利用中心差分法计算悬臂梁在随机荷载作下的结构响应数据。悬臂梁详细参数如下:长度12 m,热轧工字钢I10,面积为14.345 cm2,惯性矩为245.0 cm4,Q345钢材,杨氏模量E=206 GPa,泊松比为0.3,密度为7 850 kg/m3,取前3阶模态进行分析,每阶模态的阻尼比均取0.5%,前三阶频率分别为0.806 8 Hz,5.056 8 Hz,14.160 6 Hz,荷载由随机白噪声生成,并为结构响应添加随机白噪声。沿梁长度方向均匀设置12个加速度测点,采集频率50 Hz,时长1 200 s,加载点位于悬臂端,如图2所示。图3显示了测点Ac3的加速度时程曲线。

图2 悬臂梁测点布置
3.2 Bayesian TDD-FFT参数识别
图4显示了测点Ac3的加速度功率谱。利用AMD(Analytical Mode Decomposition)[12]法对原始数据进行滤波处理,带宽分别取0~2 Hz、4~6 Hz、13~15 Hz。利用Bayesian TDD法计算得到悬臂梁的前3阶模态振型如图5所示,从图中可看出,计算值与理论值吻合很好,表明Bayesian TDD方法能有效地识别结构振型。

图3 测点Ac3加速度时程
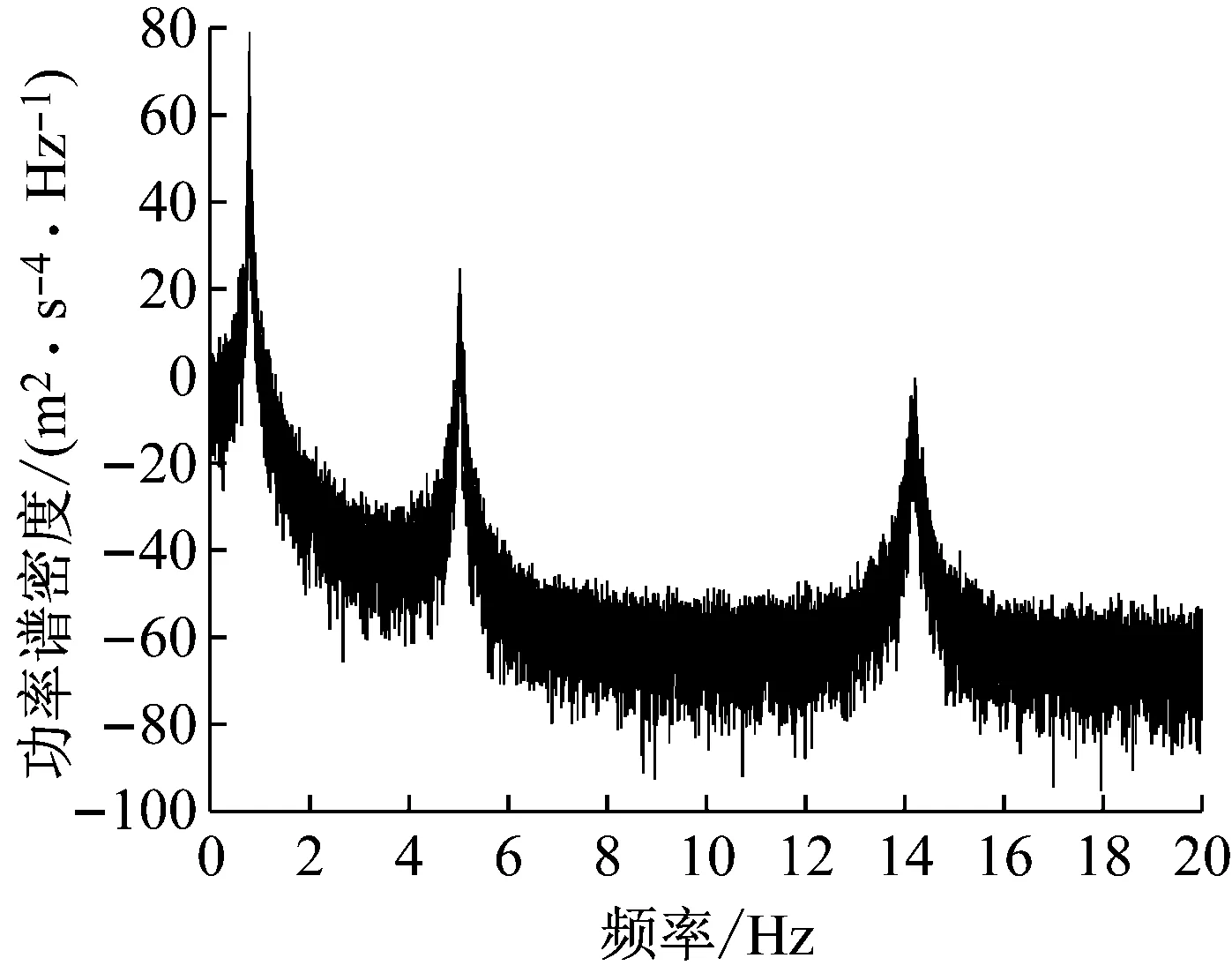
图4 测点Ac3加速度功率谱



图5 Bayesian TDD-FFT法识别出的前3阶振型
Fig.5 The first three modes identified by Bayesian TDD-FFT method
表1列出了部分模态参数的识别结果,其中,频率的识别值与理论值0.806 8 Hz、5.056 8 Hz、14.160 6 Hz很接近,阻尼比的识别值与理论值0.005也基本一致,表明Bayesian TDD-FFT方法能有效地识别结构的动力参数。从变异系数(Coefficient of Variation,COV)可以看出,阻尼比的变异系数是最高的,可见在模态识别中阻尼比的值不易准确测定。
4 工程应用
4.1 上海中心加速度响应采集系统
为了采集自然激励下的加速度数据,上海中心大厦共沿楼层高度方向共安装了71个Lance加速度传感器。加速度传感器的详细参数,见表2。
表1 Bayesian TDD-FFT模态参数识别结果
Tab.1 Modal parameters identification based on Bayesian TDD-FFT method

阶次参数频率阻尼比激励谱密度误差谱密度第一阶MVP0.807 40.004 63.823 71.798 5E-2标准差5.368 4E-34.103 2E-41.727 2E-31.490 5E-4COV/%0.664 98.920 04.517 1E-20.828 7第二阶MVP5.050 20.004 92.611 31.262 0E-2标准差0.039 44.790 4E-46.072 6E-41.503 4E-4COV/%0.780 29.855 52.325 5E-21.191 3第三阶MVP14.167 80.004 82.168 11.940 8E-3标准差0.064 763.843 8E-45.444 2E-43.655 5E-5COV/%0.457 18.007 12.511 0E-21.883 5注:变异系数COV=标准差/MPV

表2 加速度传感器参数
4.2 良态风作用下模态参数识别
2018年4月12日~14日上海浦东风速达到4~5级,尤其是4月13日的瞬时最大风速达到30 m/s,实时风速见图6。考虑到识别效果和仪器的采样精度,取风速较大时间段(13日7时~8时)的加速度数据进行模态参数识别。考虑到篇幅,本文只选取21层、36层、51层、67层、83层、100层、117层、124层的X(东西)向加速度进行识别。图7是各层加速度的样本(600 s)和117层加速度功率谱密度。

图6 2018年4月13日实时风速
利用AMD(Analytical Mode Decomposition)法对原始数据进行滤波处理,带宽分别取[0,0.17]、[0.17,0.25]。对滤波后的数据应用Bayesian TDD-FFT方法进行处理,计算结果见图8~14和表3所示。其中,图8和图9显示了前两阶模态和单自由度响应概率分布。前两阶模态与Fast Bayesian FFT求解结果相似。单自由度响应的概率密度分布与Gauss分布十分吻合,验证了Bayesian TDD假定和推论的正确性。
表3 Bayesian TDD-FFT前两阶模态参数
Tab.3 The first two order modal parameters based on Bayesian TDD-FFT method




(a) 不同楼层600 s加速度样本

(b) 117层加速度功率谱
Fig.7 Acceleration sample during the 600 s and power spectral density of 117th floor acceleration
X方向前两阶模态参数抽样样本如图10所示,MPV值见表3。由于抽样起始点是MPV值,因此抽样样本收敛在MPV值附近。从图11和图12可以看出,频率和阻尼比的后验概率密度分布与Gauss分布相吻合,而激励谱密度和误差谱密度的后验概率密度分布离散且与Gauss分布相差较大。
图13和图14为前两阶的模态参数后验联合分布直方图,从图中可看出,频率与阻尼比没有相关性,而激励谱密度和预测误差谱密度呈近似的线性相关性:预测误差谱密度与激励谱密度呈反比例关系,即噪声谱密度随着激励谱密度的增加而降低,这与信号采集时的常规认知相一致。

(a) X方向第一阶阵型

(b) X方向第一阶模态响应概率分布
Fig.8 The 1stmode shape and the probability distribution of the 1stmode response inXdirection

(a) X方向第二阶阵型
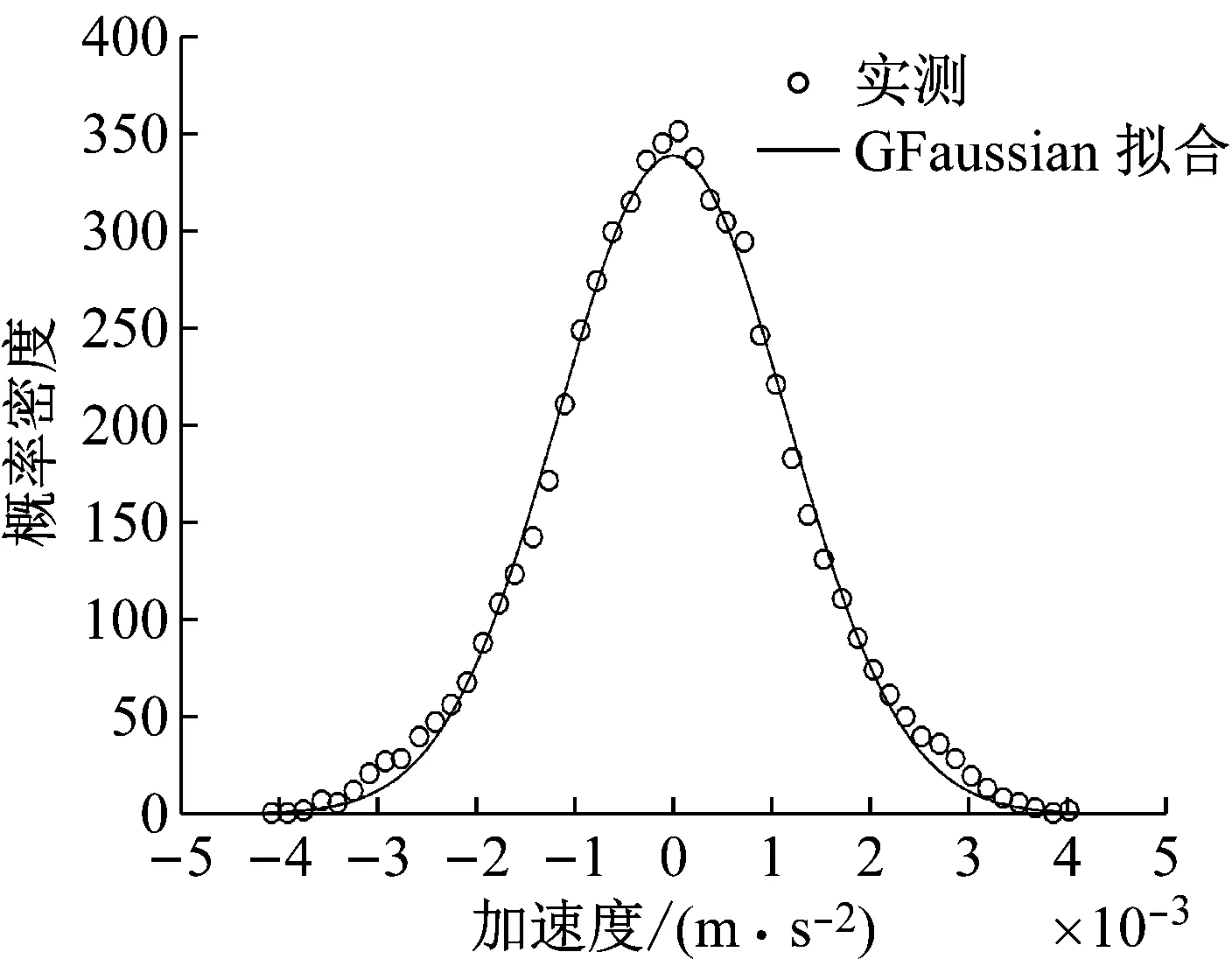
(b) X方向第二阶模态响应概率分布
Fig.9 The 2ndmode shape and the probability distribution of the 2ndmode response inXdirection

(a) 第一阶模态参数抽样样本(b) 第二阶模态参数抽样样本

图10 X向第一阶模态和第二阶模态参数抽样样本
图11 第一阶模态参数后验概率密度分布
Fig.11 The posterior probability density distribution of the 1stmodal parameters

(a) 频率后验概率分布图(b) 阻尼比的后验概率分布图(c) 激励谱的后验概率分布图(d) 误差谱后验概率分布图
图12 第二阶模态参数后验概率密度分布
Fig.12 The posterior probability density distribution of the 2ndmodal parameters
表4为应用Fast Bayesian FFT方法计算得到的前两阶模态结果,Fast Bayesian FFT法采用的滤波带宽与Bayesian TDD-FFT法相同。从表3和表4可看出:Bayesian TDD-FFT法所求得的频率和阻尼与Fast Bayesian FFT法接近,但前者的变异系数更低,结果更稳定。Bayesian TDD-FFT法所求激励谱密度大于Fast Bayesian FFT法所求值,而误差谱密度小于后者,这是由于在Bayesian TDD法处理时舍弃了部分噪声分量。表中变异系数表明,两种方法求解出的频率、激励谱密度和误差谱密度的后验不确定性小,而阻尼比的不确定性大。
表4 Fast Bayesian FFT前两阶模态参数
Tab.4 The first two order modal parameters based on Bayesian FFT method

阶次参数频率阻尼比激励谱密度误差谱密度第一阶MVP0.1060.0141.193E-066.114E-05标准差6.546E-42.206E-39.278E-81.190E-8COV/%0.6115.927.771.947 2E-02第二阶MVP0.2030.0131.226E-071.241E-06标准差3.854E-41.446E-39.526E-95.479E-12COV/%0.1910.987.764.414 9E-04注:变异系数COV=标准差/MPV
表5列出了SSI(Stochastic Subspace Identification,随机子空间)法和Bayesian TDD-FFT法识别的模态频率和阻尼比的对比结果,从表中可看出,两种方法的频率识别结果基本相同,但阻尼比的识别结果存在一定差异,进一步说明了阻尼比识别的不确定性相对较大。相比SSI方法,Bayesian TDD-FFT法的优势在于能够获得参数的后验概率分布,同时可以对参数的不确定性进行评估。
表5 Bayesian TDD-FFT和SSI方法参数识别结果对比
Tab.5 Result comparison of parameter identification using SSI and Bayesian TDD-FFT method
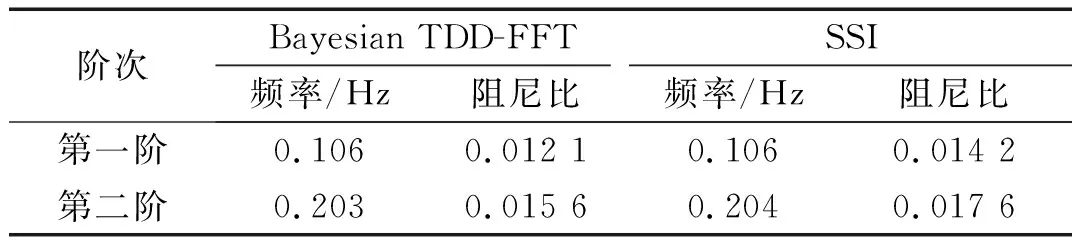
阶次Bayesian TDD-FFTSSI频率/Hz阻尼比频率/Hz阻尼比第一阶 0.1060.012 10.1060.014 2第二阶 0.2030.015 60.2040.017 6
5 结 论
Bayesian TDD法将多测点多自由度信号转换成单测点单自由度信号,有效地降低了监测信号处理的复杂程度。Bayesian TDD和蒙特卡罗方法的联合应用,避免了Bayesian FFT法中病态Hessian矩阵的求逆运算,能够有效地对结构模态参数进行评估。实际工程应用结果表明:

(a) 频率与阻尼比后验联合分布直方图

(b) 频率与阻尼比联合分布热力图

(c) 激励谱密度与误差谱密度后验联合分布直方图

(d) 激励谱密度与误差谱密度联合分布热力图
Fig.13 Posterior joint distribution histogram and hot map of the 1stmodal parameters
(1) Bayesian TDD-FFT法能够有效地识别结构的模态参数,利用蒙特卡罗抽样分析可以获得及验证模态参数的后验概率分布,此为Bayesian TDD-FFT法优于Fast Bayesian FFT法之处;
(2) 对比分析表明:Bayesian TDD-FFT法虽然是一种数值解法,但仍能够达到Fast Bayesian FFT法的解析解精度;相比SSI法,Bayesian TDD-FFT法的优势在于能够获得参数的后验概率分布,同时可以对参数的不确定性进行评估;

(a) 频率与阻尼比后验联合分布直方图

(b) 频率与阻尼比联合分布热力图

(c) 激励谱密度与误差谱密度后验联合分布直方图

(d) 激励谱密度与误差谱密度联合分布热力图
Fig.14 Posterior joint distribution histogram and hot map of the 2ndmodal parameters
(3) 上海中心大厦的实测数据分析结果表明:频率、激励谱密度和误差谱密度的后验不确定性小,而阻尼比的不确定性大;频率和阻尼没有相关性,而激励谱密度和误差谱密度存在近似的线性相关性,即反比例关系。
