双滚柱少齿差行星传动齿形综合与精度优化

张 鹏，杨 坤, 储恒超, 王章铭

(安徽工业大学机械工程学院，安徽 马鞍山 243032)

0 引言

双滚柱少齿差行星传动是一种新型传动，其采用少齿差行星传动的基本结构，具有传动比大、 功率密度高等优点. 该传动采用圆柱形滚柱作为轮齿进行啮合传动，因此较之一般少齿差行星传动，还具备齿形简单、 制造方便、 精度易于控制等优点. 若辅以合理的齿形优化设计，可实现0.017°～0.067°[1]的高精度传动，在机器人、 数控机床、 精密检测装备等领域具备良好的应用前景.

目前，国内外学者针对双滚柱少齿差行星传动进行了一些基础研究，Lai[2-3]、 陈兵奎等[4]针对双滚柱等少齿差行星传动进行了啮合理论研究，Tsukada等[5]构建了该传动的误差分析模型，刘景亚等[6]分析了该传动结构参数对传动精度的影响. 针对双滚柱少齿差行星传动，目前仍缺乏完善的齿形综合研究，尚未建立有效的精度控制及其参数优化设计方法，限制了该传动的有效设计和技术应用.

针对上述问题，基于双滚柱少齿差行星传动的啮合原理，构建了该传动齿形方程； 结合曲率分析，提出了滚柱齿形的替代方法，并利用粒子群优化算法，对齿形参数进行了优化设计，实现了对传动精度的有效控制； 最后通过传动误差分析验证了优化结果的有效性.

1 结构与传动原理

图1 双滚柱少齿差行星传动结构原理图 Fig.1 Structural of double rollers planetary transmission with small tooth number difference

双滚柱少齿差行星传动由行星轮、 中心轮所组成，行星轮外圈均布有圆柱形的行星轮齿，中心轮内圈也均布有圆柱形的中心轮齿，如图1所示. 图1中Oa为行星轮的几何中心，Ob为中心轮的几何中心，Oa与Ob之间的距离等于偏心轴的偏心距e.

行星轮安装于偏心轴上，在传动过程中行星轮随偏心轴以Ob为中心做公转运动，同时行星轮上的行星轮齿与中心轮上的中心轮齿相互啮合，反推行星轮以Oa为中心作低速自转运动，并实现动力输出.

2 齿形综合分析

2.1 双滚柱少齿差行星传动的齿形原理

2.1.1共轭齿形分析

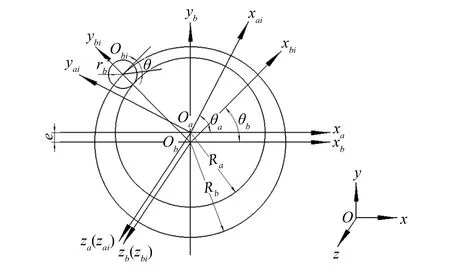
图2 定坐标系与动坐标系 Fig.2 Fixed coordinate system and dynamic coordinate system

以行星轮几何中心Oa和中心轮几何中心Ob为坐标原点，建立定坐标系Oaxayaza和Obxbybzb，如图2所示. 轴xa与xb平行，xa与xb之间的距离为偏心距e； 同时以Oa和Ob为坐标原点，分别建立动坐标系Oaxaiyaizai和Obxbiybizbi，动坐标系Oaxaiyaizai与行星轮固连，动坐标系Obxbiybizbi与中心轮固连，两动坐标系Oaxaiyaizai和Obxbiybizbi分别随行星轮和中心轮作同步转动. 图2中，θa为行星轮在Oaxaya平面内的转角，θb是中心轮在Obxbyb平面内的转角，采用偏心轴固定法，当行星轮绕其中心Oa逆时针旋转θa角度时，中心轮绕其中心Ob逆时针旋转θb角度.

在动坐标系Obxbiybizbi中，中心轮齿的第i个齿廓的位置向量Pbi可表示为

Pbi=[rbcosθrbsinθ+Rbμ]

(1)

式中：rb为中心轮齿的半径；Rb为中心轮齿在中心轮上的分布圆半径；θ为角参量；μ为中心轮齿宽.

(2)

式中：Maibi为从动坐标系Obxbiybizbi到动坐标系Oaxaiyaizai的变换矩阵，Maibi=MaibMbbi.

其中，从定坐标系Obxbybzb到动坐标系Oaxaiyaizai的变换矩阵Maib为

(3)

从动坐标系Obxbiybizbi到定坐标系Obxbybzb的变换矩阵Mbbi为

(4)

(5)

式中：m=θa/θb=Zb/Za；Za为行星轮齿数；Zb为中心轮齿数.

根据曲面单参数的包络方法[3]，可得

(6)

将式(5)代入式(6)，化简后可得角参量θ的表达式为

(7)

则与中心轮共轭的行星轮齿廓方程的一般表达式为

(8)

式(8)的行星轮齿廓方程还可以表示为

(9)

式中：ρ1为行星轮齿廓任一点的极坐标向径.

2.1.2齿廓曲率半径

利用微分中曲率半径公式，求得式(8)对应的行星轮齿廓曲率半径ρ为

(10)

式中：K1为短幅系数；K1=eZb/Rb.

式(10)中，令行星轮齿廓曲率半径的一阶导ρ′=0，可知当θb=-180° 时, 对应行星轮齿廓曲率半径的极值点.

取算例参数K1=0.69，Rb=44 mm，rb=5 mm，Zb=16，代入式(10)绘制出行星轮齿廓曲率半径ρ随转角θb的变化曲线，如图3所示. 行星轮齿廓曲率半径在极值点(θb=180° )附近的变化曲线如图4所示.

图3 行星轮齿廓曲率半径Fig.3 Radius of curvature of planetary gear tooth profile

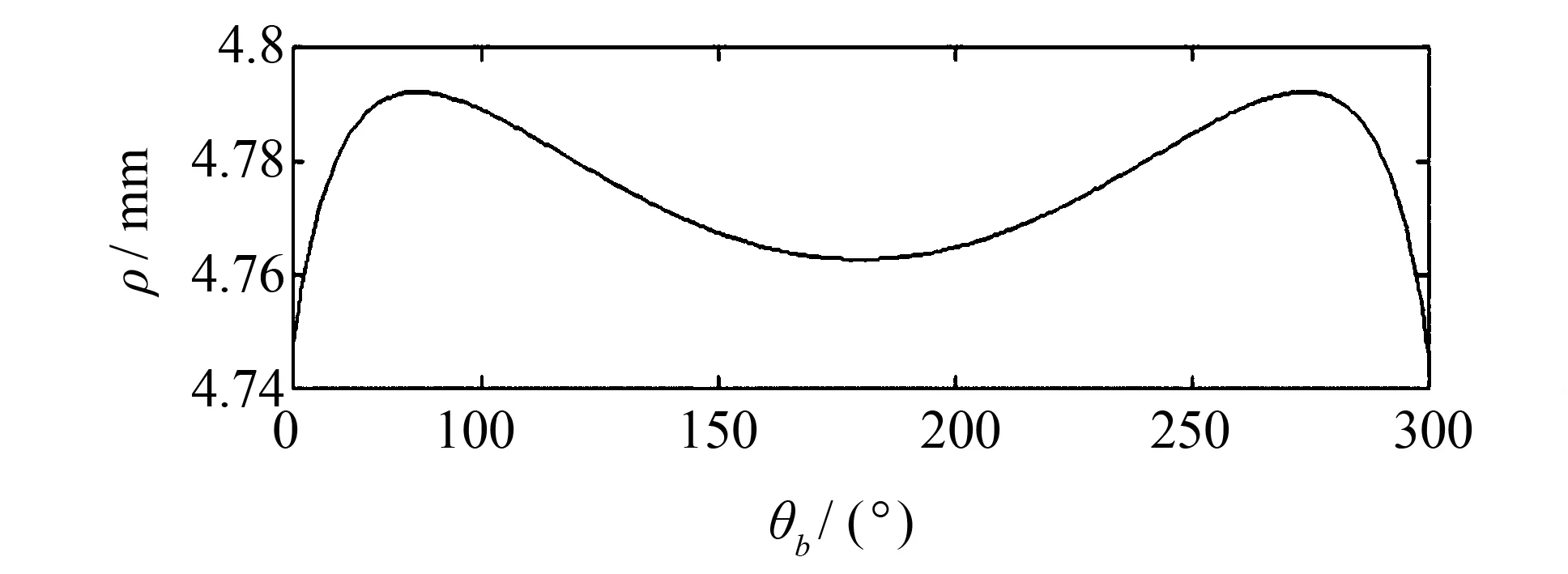
图4 极值点附近的行星轮齿廓曲率半径Fig.4 Curvature radius of planetary gear profile near extreme point

由图3、 图4可知，算例中在极值点(θb=180°) 附近，行星轮齿廓曲率半径的变化幅度仅为0.05 mm，行星轮齿廓曲线可近似于圆，因此可采用圆形滚柱作为行星轮齿.

2.2 双滚柱少齿差行星传动的齿形建模

2.2.1圆形滚柱行星轮齿的建模方法

由2.1.2的分析可得行星轮可以采用圆形滚柱作为轮齿，由于行星轮齿廓曲率半径在极值点(θb=180°) 附近变化很小，且曲率半径以θb=180°位置呈对称式分布，因此宜选取θb=180°对应的齿廓点

图5 圆形滚柱行星轮齿及其坐标系 Fig.5 Circular roller planetary gear and its coordinate system

作为圆形滚柱行星轮齿的齿顶点. 同时，为防止干涉，圆形滚柱行星轮齿半径应小于等于θb=180° 对应的齿廓曲率半径值. 为进一步减小齿形替代误差，优先选取圆形滚柱行星轮齿半径等于θb=180° 对应的齿廓曲率半径，将θb=180°代入式(10)，可得行星轮齿的半径ra为

(11)

圆形滚柱行星轮齿及其坐标系如图5所示，圆形滚柱行星轮齿与行星轮齿廓在θb=180° 处相切，切点坐标为(xA，yA). 由式(8)可得(xA，yA)的表达式为

(12)

由于圆形滚柱行星轮齿的圆心(xa，ya)与(xA，yA)距离为ra，可得圆形滚柱行星轮齿的圆心(xa，ya)表达式为

(13)

2.2.2圆形滚柱行星轮齿的齿形方程

由式(11)～(13)可得极坐标形式的圆形滚柱行星轮齿的齿形方程为

(14)

3 齿形精度优化

用圆形滚柱替代行星轮齿廓进行啮合传动，仍然存在一定的齿形误差与传动误差，需进行齿形参数优化设计，以减小齿形误差，从而实现齿形的精度控制，达到精密传动的要求.

3.1 设计变量

选取对传动精度有显著影响的齿形参数作为设计变量，相应齿形参数包括短幅系数K1、 偏心距e、 中心轮齿数Zb、 中心轮齿半径rb、 行星轮齿半径ra、 中心轮齿分布圆半径Rb和行星轮齿分布圆半径Ra.

3.2 目标函数

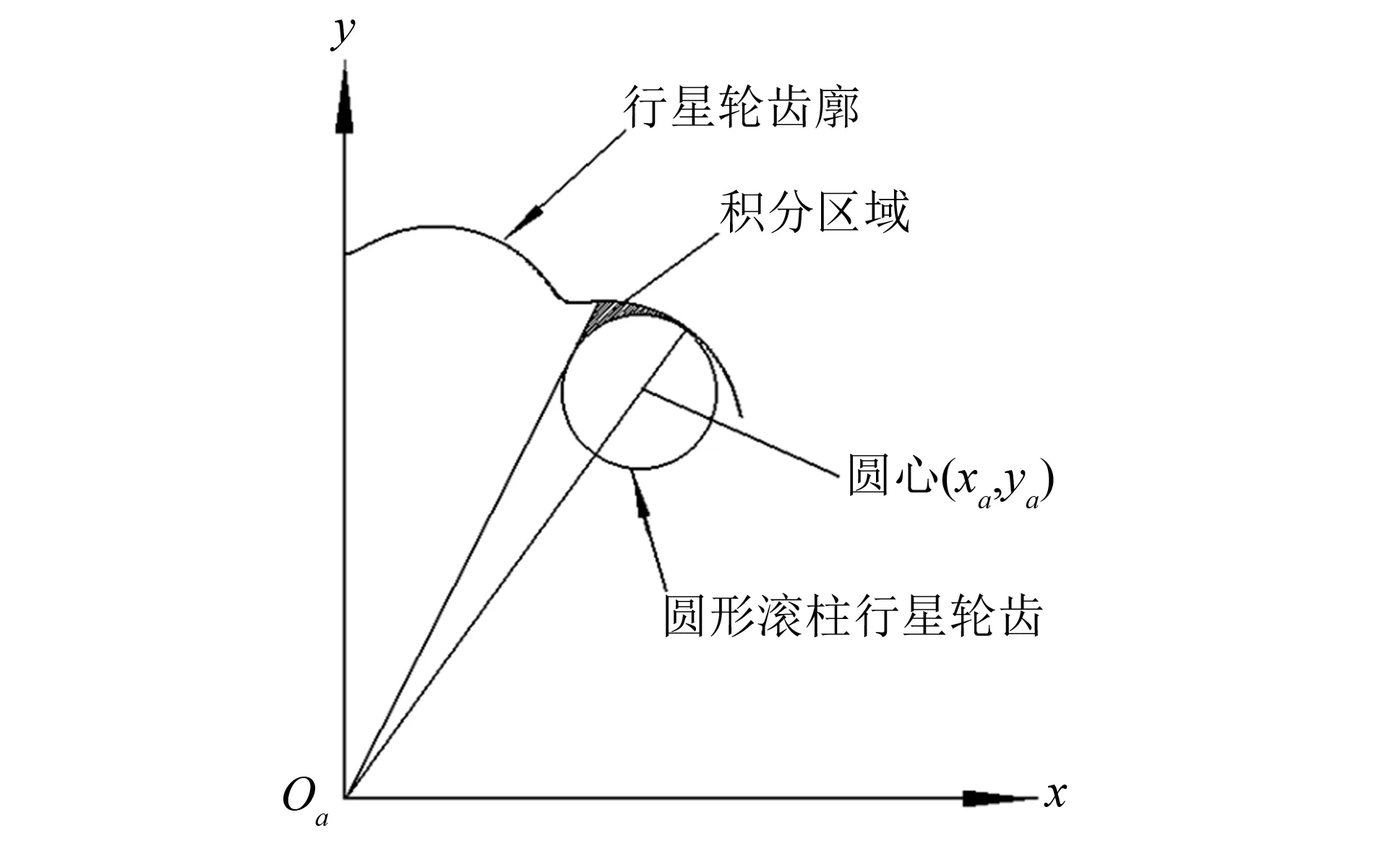
图6 目标函数的几何表达Fig.6 Geometric representation of objective function

为使齿形替代误差尽可能小，以圆形滚柱行星轮齿与行星轮齿廓的径向差值的积分为目标函数进行优化，选任一对轮齿建立分析模型, 如图6所示. 为将优化范围控制在有效啮合区内，积分区间上限为圆心(xa，ya)与原点Oa连线，积分区间下限为过原点Oa的圆形滚柱行星轮齿的切线，即图6所示的阴影区域.

目标函数F的表达式为

(15)

式中：c为积分区间上限对应的相位角，c=nπ/Za，(n=0，1，2，…,Za)；d为积分区间下限对应的相位角，d=c+Zaarcsin[ra/(Rbe-ra)] .

3.3 约束条件

表1 短幅系数K1的优选范围

目标函数中设计变量需满足一定的约束条件，考虑齿形根切[7]、 接触应力[8]、 传动结构等因素，得到如下约束条件为：

1) 短幅系数K1随齿数Za的优选范围[9]如表1所示.

2) 为尽量减小接触应力，ra、rb取值为

(16)

3) 根据少齿差行星传动结构尺寸关系，可得

Ra=Rb-ra-rb+e

(17)

(18)

3.4 优化计算

粒子群优化算法[10]在求解优化函数时，表现出较好的寻优能力，特别是针对复杂的工程问题，通过迭代寻优计算，能够迅速找到近似解，因此粒子群算法在工程计算中应用广泛.

选取Zb=24，Zb=60，Zb=88，以式(15)为目标函数，结合式(16)～(18)及表1的约束条件，运用粒子群优化算法，求得使目标函数F→min时的齿形参数优化结果，如表2所示.

表2 齿形参数优化结果

4 误差分析

4.1 误差公式

将表2所得优化结果代入传动误差公式进行分析. 建立双滚柱少齿差行星传动啮合过程中几何尺寸关系图，如图7所示.

图7 双滚柱少齿差行星传动几何关系Fig.7 Geometric relationship of double roller planetary transmission with few teeth difference

θai为行星轮上的第i个齿与其中心连线和偏心轴之间的夹角，θbi为中心轮上的第i个齿与其中心连线和偏心轴之间的夹角；Oai为行星轮上的第i个滚柱的圆心，其坐标可表示为(Rasinθai，Racosθai+e)，Obi为中心轮上第i个滚柱的圆心，其坐标可表示为(Rbsinθbi，Rbcosθbi)；d为OaiObi之间的距离.

根据文[5]，可得双滚柱少齿差行星传动的传动误差Δθ为

(19)

式中：

4.2 实例计算

将表2中的三组齿形参数优化结果代入式(19)，分别得到误差分析结果如图8所示.

图8 传动误差Fig.8 Transmission error of data

由图8可知，当Zb=88，K1=0.8，e=1时，Δθ可控制在0.060 6°以下，一般摆线针轮减速器的传动精度为0.050°～0.067°[11]，即双滚柱少齿差行星传动能够满足精密传动的要求. 根据文[1]，同等设计参数下，滚柱式减速器的传动误差值约为0.06°，与数据组Ⅲ计算的理论传动误差值基本一致. 与同等条件下的一般渐开线齿轮减速机传动误差[12]相比，数据组Ⅲ计算的传动误差值降低了约50%.

5 结语

1) 建立中心轮和行星轮的共轭齿廓方程，对齿廓方程进行曲率分析，确立圆形滚柱行星轮齿的齿形方程，并进行精度优化设计，验证了双滚柱少齿差行星传动作为精密传动的可行性.

2) 由于行星轮齿廓曲率半径变化小，可以使用圆形滚柱替代行星轮齿廓，再结合优化设计，可实现0.067°以内的精密传动，因此双滚柱少齿差行星传动能够适用于精密传动场合.

3) 中心轮齿数Zb较大时，传动误差Δθ相对较小，可以实现精密传动，因此双滚柱少齿差行星传动更适宜较大传动比的传动场合.