快速路行车安全的可变限速方法

林奕钦，王伟智

(福州大学土木工程学院，福建 福州 350108)

0 引言

城市快速路在城市交通中拥有越来越重要的地位，合理的限速值可促使驾驶员行驶在一定的安全速度范围以内，从而提升快速路上的行车安全. 以往道路限速值是以自由流状态下85%的车速作为基本依据，再结合道路线型等因素进行修正，限速值确定之后一般不会改变，其本质属于静态限速. 而城市快速路有别于全封闭的高速公路，外部干扰较多，交通流运行较复杂，固定的道路限速值在复杂的交通环境下难以为驾驶员提供安全合理的限速，因此，传统的限速值确定方法具有很大的局限性.

可变限速(variable speed limits，VSL)控制是通过检测交通流参数从而对道路交通流进行实时的监控，在适当的时候启用可变限速控制来保证交通流高效、 安全的运行，其本质是动态限速，能很好地对道路交通流的运行进行实时控制. 国外较早开始可变限速方面的研究，相关方法已开始应用到实际的道路中. 众多研究表明： 可变限速控制策略能够有效地提升交通安全水平[1-5]. 文献[1]能够降低碰撞几率和冲突数，文献[3]通过减少车道内和跨车道以及上下游之间的速度变化来改善交通安全，达到减少事故数量的目的. 文献[4]建立了合流区和警告区限速模型，在通行能力变化不显著的情况下，模型计算的限速方案使平均速度有所降低，同时也降低了最大排队长度和速度标准差，提高了事故现场路段的安全性. 文献[5]将可变限速方法应用于高速公路入口匝道瓶颈上游路段，以减少因运动波传播而引发的追尾事故，起到了提高交通安全的目的.

以往大多数可变限速研究都是针对通行效率进行改善，而道路上一旦发生交通事故，不仅会影响通行效率，更重要的是可能会造成财物损失或人畜伤亡. 所以，针对交通安全的可变限速研究具有更重要的意义.

本研究基于碰撞时间(time to collision, TTC)，构建了针对行车安全的快速路可变限速优化控制模型. 以TTC作为可变限速控制的启动阈值，能够实时对交通流的事故风险进行预测，同时在动态交通流模型的基础上构建了基于TTC的限速值优化计算模式，对可变限速方法进行了优化. 仿真实验也说明本研究提出的方法能够为基于安全的可变限速控制提供参考.

1 可变限速对交通安全影响机理

可变限速对交通安全的影响并非简单降低交通流速度，速度的绝对值会直接影响事故的严重程度，而速度离散度才是影响事故发生的关键因素. 可变限速控制通过对速度产生影响，从而对交通流密度、 流量等参数也产生影响，并引起交通流运行状态向期望的方向改变与转移. 可变限速在对交通安全进行调控的同时，还能降低交通流的速度离散度以及减少车辆换道等，提升交通安全的同时也能避免或者降低通行能力下降的现象，可提高通行效率，并保证了交通流运行的稳定.

可变限速控制通过改变路段内的车速从而减少速度方差，平稳车辆间的车头时距，保证了路段交通流的稳定性. 同时，可变限速控制降低了下游路段的流量，减少了车辆间的相互干扰，提升了交通安全水平. 本质上，可变限速控制通过对交通流进行调控，从而间接对交通安全产生影响，可变限速控制在判断交通事故风险的基础上，通过调节限速值对交通流状态进行主动干预，从而增强快速道路行车安全性.

2 交通安全风险预测模型

快速路的交通安全调控要先对实行可变限速的路段制定实时事故风险预测模型. 传统交通事故风险预测模型大都需要路段上大量的事故数据以及非事故数据来进行模型构建，由于交通事故的发生具有小概率、 偶然性的特征，某些新建路段常常缺少交通事故的历史数据. 此外，传统的事故风险预测模型往往没有直接考虑交通流的运行特性，而是通过对事故数据进行逻辑回归来进行建模，将会存在一定的局限性和不准确性. 因此，本研究充分考虑交通事故发生前的交通流运行特性，将采用基于交通冲突的事故风险预测模型.

2.1 交通冲突的描述

快速路交通流特性较复杂，交通流运行干扰较多，常见的快速路交通冲突描述如图1所示. 在图1(a)中，当后车速度大于前车时，后车一旦遇上瓶颈导致当前车道无法通行时，如果后车驾驶员没能提前发现瓶颈并采取避险措施时，就只能进行强制换道进行避险，由于速度大于前车，极其容易在箭头交汇处产生一个冲突，严重的时候甚至会造成交通事故. 在图1(b)中，也假设后车速度大于前车，当前车遇上瓶颈难以通过换道进行避险时，必然采取紧急刹车行为，后车如若没有采取避险措施则会发生追尾事故.

图1 常见快速路冲突类型Fig.1 Common types of conflicts on expressway

2.2 交通事故风险预测模型构建

交通冲突的判别方法通常有空间距离法、 时间距离法、 能量判别法. 快速路上的交通事故通常是由于驾驶员对与其他交通个体之间的安全距离把握不当，当有紧急情况发生的时候，来不及采取避险措施而导致交通事故的发生. 因此本研究的交通事故风险预测模型利用测量车速、 车辆通过检测断面的时间以及车辆所处车道这三个检测参数，并通过推测TTC进而预测路段上发生交通事故的风险. TTC是道路使用者逼近相撞点的实际速度与距离的时间矢量对事故点的投影，其综合反映了距离和速度的因素. 研究表明： 基于TTC的可变限速方法能克服现有限速方法的不足[6].

在非失控状态下，车辆一般只会与本车道或相邻车道的车辆产生交通冲突，且后车速度大于前车，即两辆车处于不断接近的状态. 考虑两种情况，即追尾冲突及换道冲突. 对于通过检测断面的前后两车，当后车速度大于前车车速时，对于两车之间的TTC可按照下式计算：

(1)

式中：vn为第n辆车通过检测断面时的车速，m·s-1；tn为第n辆车通过检测断面时的时间；θ为指示通过检测断面前后两车相对位置的参数，取0或1，取0表示两车位于同一车道，取1表示两车位于相邻车道.

一般而言，TTC≤3 s时即认为是一次严重的有可能导致交通事故的冲突. 将一个控制周期内通过检测断面前后两车之间的TTC按照从大到小的顺序排列，当第85%位的TTC≤3 s时，即启动可变限速控制来降低路段内发生交通事故的风险.

随着人口老龄化的不断加剧，养老问题成为一大难题。我国人口老龄化易呈现家庭小型化、空巢化，养老模式由单一的家庭养老逐步向多样化的社会化养老演变。

3 基于TTC的可变限速控制优化模型

3.1 快速路动态交通流模型

图2 可变限速控制路段划分 Fig.2 The road section of the variable speed limits control

为准确描述快速路交通流的动态传播过程，将快速路划分成N个基本路段(如图2)，每个基本路段具有一致的基本属性. 对第k控制周期内基本路段i的流率qi(k)进行预测，其表达式为：

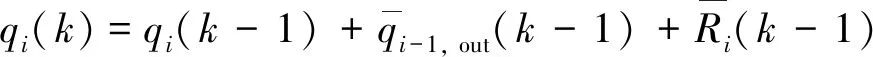
(2)

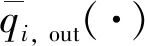
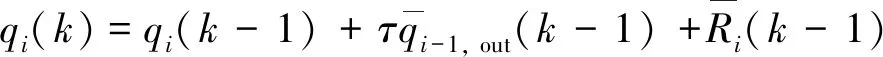
(3)

式中：τ为影响系数，表示对基本路段i流出率的影响.

(4)

此时基本路段i内的密度为：

(5)

式中：T0为检测周期；Li为单位基本路段的长度；ωi为基本路段内的车道数.

相关学者已经构建了适用于各种交通负荷下的车速—流量模型[8]，通过其模型求出第k控制周期存在瓶颈区域的基本路段i的交通流期望车速vd, k(k)为：

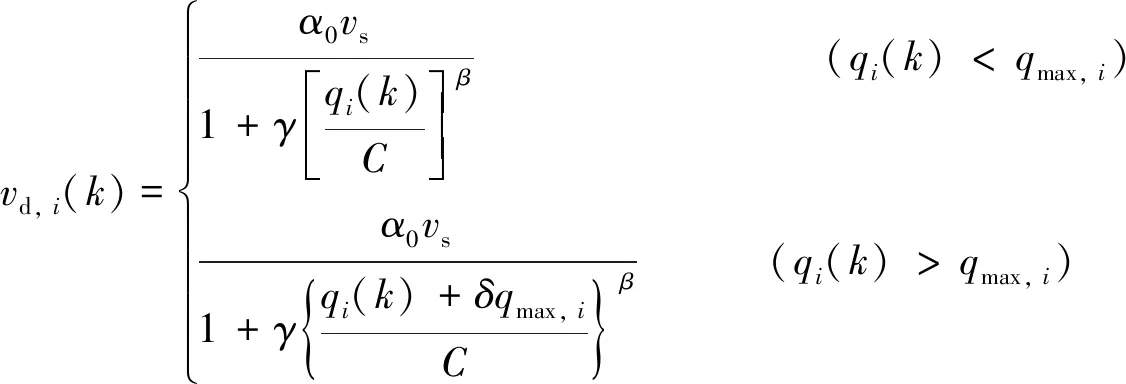
(6)

式中：α0，β，γ为修正系数；vs为设计车速；C为路段通行能力.

3.2 基于TTC的可变限速值计算

传统可变限速方法大都基于动态交通流模型来计算可变限速值[6-7]，随着时间推移或环境因素的改变，交通流与动态交通流模型的拟合度可能会降低，基于动态交通流的可变限速值并不能准确地对交通流进行控制，需要定时对动态交通流的拟合度进行校验. 交通冲突技术是新兴的交通安全相关技术，在国内外的实践、 研究中都表明交通冲突能够替换事故，从而作为一种独立的方法用于交通安全的评价. TTC通过对交通流的车辆运行速度及轨迹进行实时分析计算，对不同交通流条件及环境因素下的交通流运行状态都能进行准确的判断. 基于TTC的限速值计算能够优化在动态交通流模型基础上的可变限速值，适应实时的交通流状态，保障行车安全. 在国际上通常将TTC小于3 s定义为严重冲突，此时在下游的交织区域或瓶颈区域两车易发生交通事故. 当TTC≥3 s认为是可以接受的状态，两边取等号计算出基于TTC的限速值vTTC为：

(7)

此时基本路段i的可变限速值vl, i为：

vl, i(k)=min{vd, i(k),vTTC, i(k)}

(8)

3.3 优化控制函数

在以安全为目标的可变限速控制中，也应尽量保证路段的通行效率，不能以通行效率为代价来提升交通安全. 可采用总延误时间(total delay time, TDT)最小和总通行交通量最大为优化控制目标，构建如下优化控制目标函数：

(9)

式中：α1，α2为总延误时间TDT和总通行交通量的权重系数；Nm，kp分别为基本路段数，控制周期内的时间步长数；tq(i)为第i辆车的排队时间，s；T0为控制周期时间；Li为单位基本路段的长度，m. 为了使可变限速控制更加合理地对交通流进行控制，需要为可变限速控制构建几个约束条件.

1) 车速极值约束. 可变限速控制的限速值既不能超过路段限速值的最高限速值也不能低于路段限速值的最低限速值.

2) 可变限速改变幅度约束. 可变限速控制的改变幅度不能过大，相邻的两次限速值改变幅度一般不能超过20 km·h-1，且为10的倍数.

3) 相邻路段可变限速改变幅度约束. 相邻两个基本路段之间的可变限速改变幅度不能超过20 km·h-1，改变幅度过大使得驾驶员需要更大的减速度来达到限速值，极易对交通流产生扰动，影响基本路段内的交通安全.

4 仿真实验分析

4.1 数据采集

本研究采集了2018年10月15日高峰期17:00—18:00福州三环快速洪塘大桥下道路施工瓶颈路段的交通流数据(包括高峰时段的交通量及车速数据)，并依照调查的数据对模型参数进行拟合，得到车速与流量的函数关系式为：

(10)

以福州市三环快速路为例，在VISSIM微观仿真软件中模拟一段长约200 m的快速路施工瓶颈，如图3所示. 代入调查的交通流数据，取100仿真步长为一个的数据获取周期.

图3 福州市三环快速仿真场景Fig.3 Simulation scene of the Fuzhou expressway

4.2 评价指标

既有研究表明, 路段车速离散度和路段交通冲突等级存在显著的正相关性，可作为交通安全评价的间接指标，选取车速均方差作为评价交通安全水平的指标. 同时构建“跟车距离速度比”的评价指标，以路段平均跟车距离与路段平均车速的比值作为评价指标，该指标能够表明在不同速度下的跟车距离的安全性，指标值越大表明此速度值下对应的跟车距离越安全. 其表达式为：

(11)

4.3 仿真结果

图4为可变限速路段内的冲突数统计，路段1～6分别表示可变限速控制区上游、 可变限速控制区、 过渡区、 合流区、 瓶颈区、 分流区. 从图4中可以看出在可变限速控制区，由于可变限速的影响，可变限速控制状态下的路段冲突数大于无控制路段，随后在可变限速平滑交通流的作用下，可变限速控制下的路段冲突数都小于无控制路段. 路段5为瓶颈区上游的合流段，可以看出交通冲突在路段4、 5内急剧增加，因为在路段5内由三车道突变为两车道，导致冲突数量急剧增加. 可变限速路段内总冲突数量为546次，较无控制状态下的573次改善了4.71%.

瓶颈上游路段车速分布见图5，从图5中可以看出无控制状态下交通流的整体通行速度较高，然而其速度异常值(红色加号)远多于可变限速控制下的合流段，交通流处于极不稳定的状态，其原因是车速离散度大，车辆间的相互干扰较多. 而可变限速状态下，虽然整体通行速度降低了，合流段的车速极差较无控制状态下也增大，其原因为可变限速降低了路段的整体车速，造成了个别车辆的较低车速，但可以明显看出可变限速控制下的合流段速度异常值显著减少，提升了路段交通流的稳定性和安全性.

表1是仿真评价数据，从表1可以看出，可变限速降低了合流段的车速均方差，提高了跟车距离速度比，有效改善了行车的安全性. 在改善交通安全的同时，总排队时间显著降低，改善了通行效率，其总通行车辆数则没有因可变限速而产生影响. 由此可见, 本研究提出的可变限速控制方法在有效提高交通安全的同时还能不影响车辆的通行效率，起到节约资源保护环境的作用.

表1 仿真评价数据

5 结语

针对城市快速路的特殊性，本研究以交通安全为主要考虑因素提出了一个可变限速优化控制模型. 同时，为了避免传统模型的逻辑回归预测交通事故风险的局限性，提出了基于碰撞时间TTC的交通事故风险阈值预测模型，给出了基于TTC的可变限速值的优化计算方法. 以福州市三环快速路为例，利用VISSIM微观仿真软件对改进的可变限速方法进行了验证. 实验结果表明, 可变限速方法能够有效降低速度离散性，减少冲突次数，可提升路段的交通安全水平，同时还能减少总排队时间，对路段的通行效率也影响较小.