基于回归分析的公路货运量预测

薛方，苏芮锋，杨升，姚远征，张俊

（陕西重型汽车有限公司，陕西 西安 710200）

前言

公路货运量反应了国民经济水平，同时也是重卡销量的基石。国内很多学者都对公路货运量进行过相关的分析，可概括为：（1）基于公路货运量统计方法的研究：梁仁鸿、仵思燃研究了公路货物运输量统计新试行方案问题及完善思路[4]；张忠民做了公路货物运输量统计方案完善与应用研究[5]；孙磊磊、李琼提出了公路运输量统计中的计量误差分析[6]；刘拥华等人提出了高速公路货物运输量统计方法[7]。（2）基于调查方法的研究：于丹阳等人提出了北京市公路货物运输量抽样调查分析与建议[8]；郭红霞、栗庆耀提出了公路货运量统计调查方法的改进[9]；张志俊、周娅提出了满足多层次需要的公路运输量抽样调查方法[10]。（3）基于公路货运量预测的研究：王俊波提出了组合预测方法在公路运输量预测中的应用研究[11]；吴凤山、范林业做了中国公路货物运输量的长期预测[12]；瞿尔仁等人做了公路运输量预测的综合时序分析[13]。

公路货运量预测是制定公路运输业发展规划和重卡销量研究的基础。本文从宏观上影响公路货运量的因子出发，首先利用散点图分析各因子和公路货运量之间的关系，然后用逐步回归法剔除掉对公路货运量不显著的因子，建立了多元线性回归方程对货运量进行预测。经检验预测模型拟合效果好。

1 公路货运量预测模型分析

公路货运量，如下图所示。货运量数据呈现上升趋势，且跌宕起伏，是一条折线，用一条直线或者曲线是描述不清楚的。因此需要考虑使用多变量预测模型。

表1 2010-2017 年货运量统计

图1 公路货运量随着年份的变化趋势

表2 2010-2017 国内生产总值、国民总收入、第一产业增加值、第二产业增加值

经过严格的分析可知，与货运量相关的可以获取到的数据有：国内生产总值，国民总收入，人均国内生产总值，工业增加值，建筑业增加值，批发和零售业增加值，交通运输、仓储和邮政业增加值，第一产业增加值，第二产业增加值，第三产业增加值这10 种数据。

表3 2010-2017 第三产业增加值、人均国内生产总值、工业增加值、建筑业增加值

表4 2010-2017 批发和零售业增加值、交通运输、仓储和邮政业增加值

1.1 模型选择

能否使用线性回归模型，要先分析自变量和因变量之间是否有线性关系，最常见的方法是散点图法，画出自变量和因变量之间的二维散点图，进行观察，如果呈现线性关系，就用线性回归，如果呈现非线性关系，就使用非线性函数来进行非线性回归。

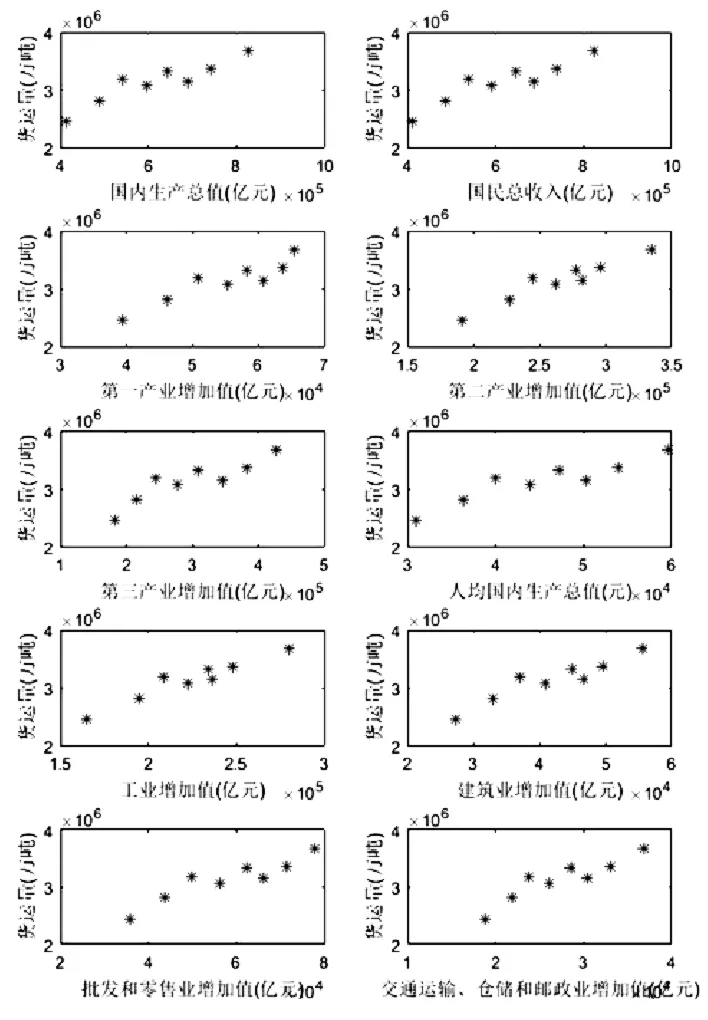
图2 公路货运量随着各个因子的变化趋势

观察图2 中的散点图，可见各因子对公路货运量的影响不是直接的线性但是可以近似为线性关系。因此可以建立多元线性回归模型求解。

1.2 因子选择

这10 个因子对公路货运量的影响程度决定了回归模型的优劣。通常情况下，如果方程中含有对因变量不起作用或者作用极小的自变量，也就是不显著的自变量，会造成回归方程预测效果下降，因此先使用多元逐步回归法对因子进行选择。

逐步回归的思想是有进有出。引入一个自变量，对已引入的变量要进行逐个检验，当原引入的变量由于后面变量的引入而变得不再显著时，要将其剔除。引入一个变量或从回归方程中剔除一个变量为逐步回归的一步，每一步都要进行F 检验，以确保每次引入新的变量之后回归方程中只包含显著的变量。这个过程反复进行，直到既无显著的自变量引入回归方程，也无不显著的自变量从回归方程中剔除为止。这样就可以保证最后所得的变量子集中的所有变量都是显著的。经过若干步以后可得到“最优”变量子集。

使用MATLAB 工具箱中的stepwise 命令进行因子选择，结果见表5。

表5 因子选择的结果

2 多元线性回归模型

回归分析预测法，是在分析了自变量和因变量之间相关关系的基础上，建立变量之间的回归方程，并将建立的回归方程作为预测模型。根据自变量的变化来预测因变量的变化，变化关系一般为相关关系。回归分析预测法主要是对具有因果关系的变量进行分析预测。回归分析所建立的模型，只有通过了各种检验，并且预测误差很小，才能应用到实际的预测中。

根据模型中自变量个数的多少，可以将回归模型分为一元回归模型和多元回归模型；根据模型是否是线性的，可分为线性回归模型和非线性回归模型。本文主要使用了一元和多元线性回归模型。

2.1 一元线性回归模型

一元线性回归只涉及一个因变量y 和一个自变量x，用x的线性函数对y 建模，即y=a+bx，其中a,b 称为回归系数对应的直线称为回归直线。在用一元线性回归模型进行预测时，首先必须对a,b 进行评估。一般采用最小二乘法。根据最小二乘法得到的参数估计值为：

式中，xi，yi是已知的历史数据，x，y 是自变量和因变量的算数平均值。考虑到随机因素的影响，可以加入随机干扰项ε，一般假定服从正态分布，且各εi互不相关。一元线性回归预测模型为：yi=a+bxi+εi。

2.2 多元线性回归模型

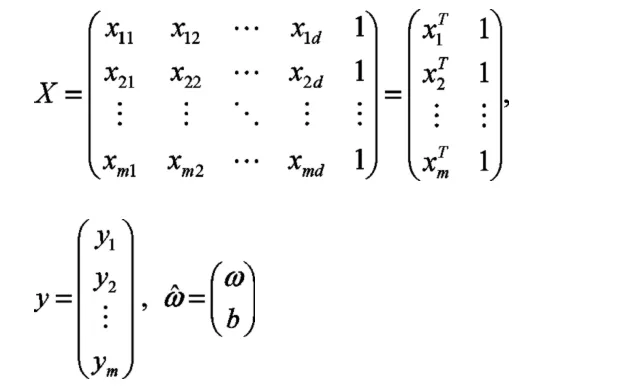
用最小二乘法求解ω 和b

当XTX 为满秩矩阵或正定矩阵时，另上式为零可得：，其中（XTX）-1是矩阵（XTX）的逆矩阵，令，则最终学得的多元线性模型为。

3 模型求解及短期中期预测

3.1 模型求解

对货运量y 与国民总收入、人均国内生产总值、工业增加值、建筑业增加值、批发和零售业增加值、交通运输、仓储和邮政业增加值这6 个因子建立6 元线性回归模型：

其中，

应用最小二乘法解得：

得到模型的回归系数

其中β0为常数项，β1,…,β6为各因子系数。因此该模型的函数表达式为：

x1,…x6依次为国民总收入(亿元)，人均国内生产总值(元)，工业增加值(亿元)，建筑业增加值(亿元)，批发和零售业增加值(亿元)，交通运输、仓储和邮政业增加值(亿元)。为货运量预测值。

预测结果见表6。

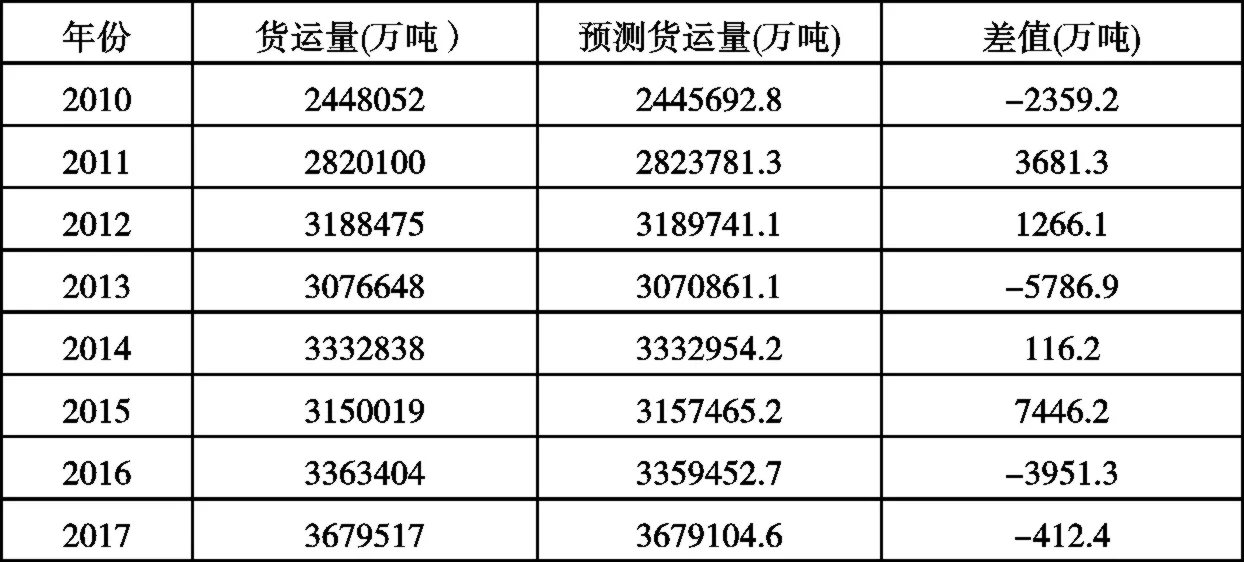
表6 多元线性回归模型预测结果

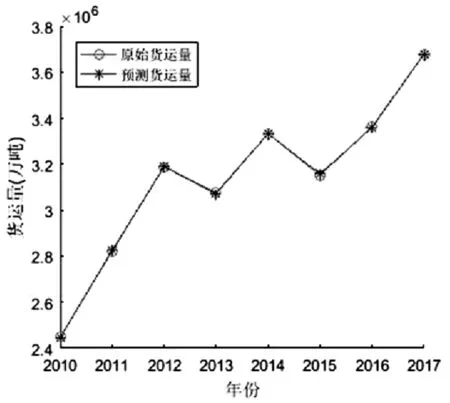
图3 原始货运量与预测货运量的曲线图

3.2 模型检验

对回归模型进行检验，结果见表7。

表7 检验结果

该模型使得p=0.02137＜0.05，样本可决系数R2=0.99987，接近于1，因此模型的拟合效果较好。

3.3 短期预测

要对未来1 年或者未来2-5 年的货运量进行预测，只需要在模型中输入自变量的值，就可以求得。但是本文自变量的数据来源于国家统计局，统计局的数据是根据真实数据测得的，因此不可能提前得知自变量的真实值。

所以需对6 种自变量进行预测，根据因子的变化趋势可知，各因子的变化和年份成一元线性关系，因此可以建立一元线性模型，分别对各项因子进行预测。预测结果见表8。使用一元线性回归模型预测的结果和原始值的对比图见图4。

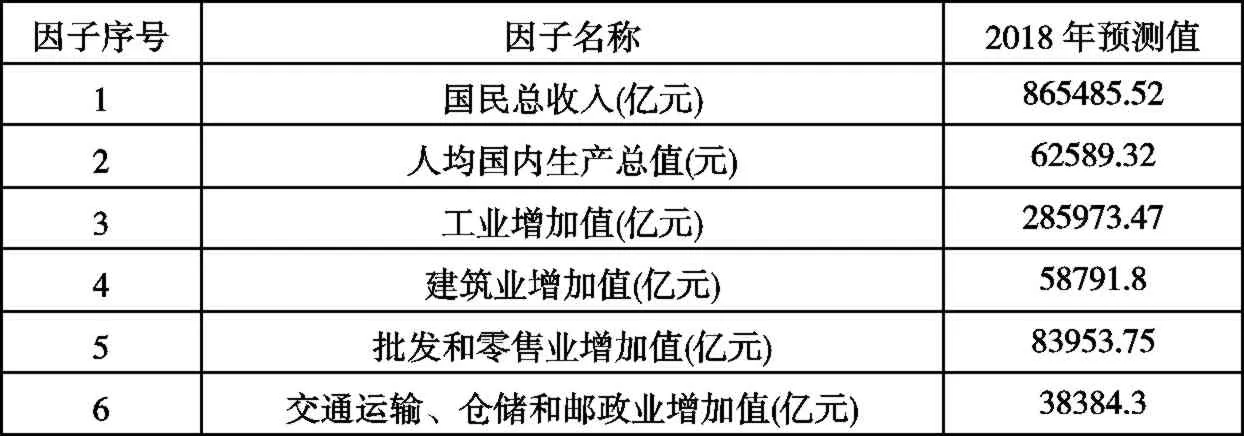
表8 2018 年各因子的预测值

图4 各因子原始值与预测值的曲线图

将2018 年各因子的预测值代入货运量预测模型可以求得2018 年的货运量为：3747247.95 万吨。

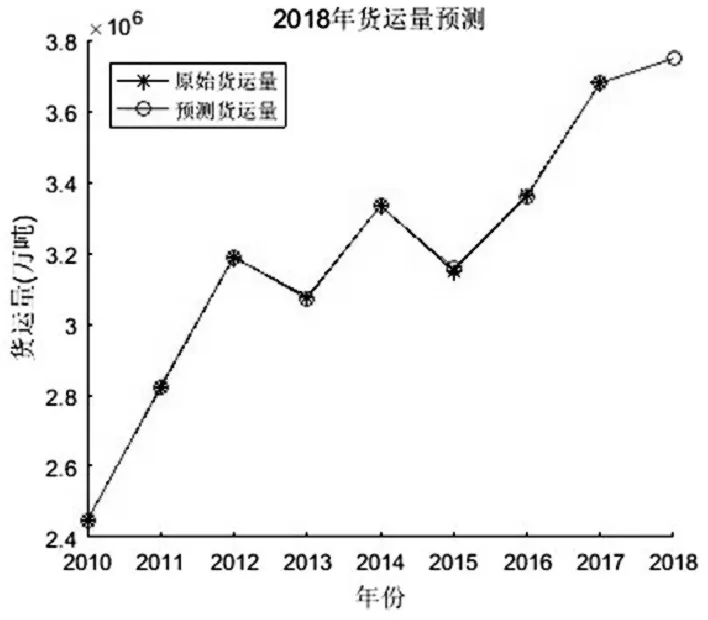
图5 货运量预测结果曲线图

4 结论

本文以中华人民共和国交通运输部公开的公路货运量数据为基准，结合国家统计局公开的年度数据搭建多元线性回归预测模型来预测未来某时段的公路货运量，模型可行性较好，预测效果优。

不足之处：各因子都近似为线性模型，如果可以找到一种非线性的函数形式替换效果估计更好。