组合KdV-Burgers方程扭状孤波解的渐近稳定性

邓升尔， 张卫国

（上海理工大学 理学院，上海 200093）

1 问题的提出

组合KdV-Burgers方程是非线性研究领域重要的模型方程，在等离子体物理、量子场理论以及固态物理中有着广泛的应用[1-6]。其中，，，是非线性项系数。当，，给定一些值时，方程（1）可以改写成其他著名的非线性方程。例如，当，方程（1）即为人们熟知的KdV-Burgers方程

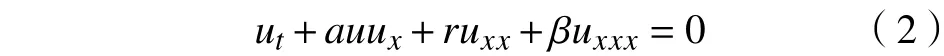
方程（2）可作为许多具有某种耗散作用的实际问题的控制方程，如粘性液体中的浅水波、弹性管内液体的流动和波动、等离子体中的磁声波等。当方程（2）中，则为著名的KdV方程

文献[7-10]研究了方程（1）孤波解的求解问题，在文献[7]中求出了方程（1）的扭状孤波解；文献[8-9]分别运用齐次平衡法和直接法与假设法的一种结合得到了方程（1）的精确解；随后，文献[10]应用Liapunov稳定性分析法证明了广义组合KdV-Burgers方程的扭状孤波解是线性稳定的，并得到了孤波解线性稳定的条件。文献[11]研究了组合KdV-Burgers方程（1）行波解与耗散系数的关系，找到了2个临界值，，，，分别为的3个实根，，，，并给出了引理1。

文献[11]利用平面动力系统的理论和方法研究了方程（1）的行波解。对于引理1中涉及的方程（1）的衰减振荡解，文献[11]利用解轨线在相图中的演化关系、假设待定法，求出了方程（1）衰减震荡解的近似解，进一步得到了近似解与真解间的误差估计，证明了误差是以指数形式速降的无穷小量。对于引理1中方程（1）所具有的波形函数为单调的行波解（也可称为扭状孤波解），目前尚未发现有对它的稳定性研究的文献发表。本文研究当时方程所有的单调递减行波解的渐近稳定性。

2 方程（1）单调递减扭状孤波解的基本性质

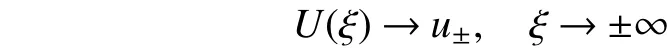
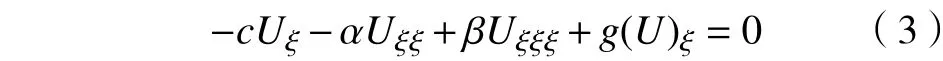
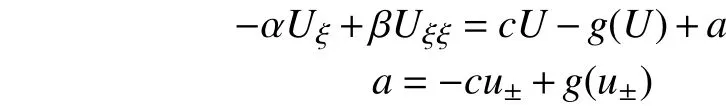
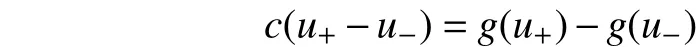
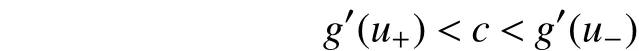
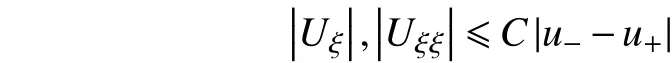
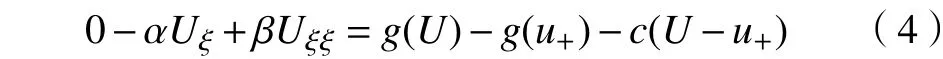
利用积分中值定理，将式（4）化为

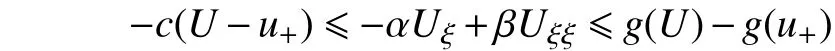
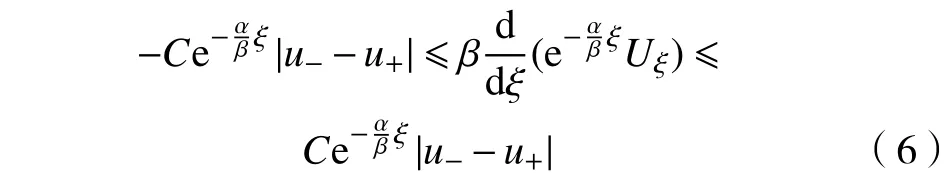
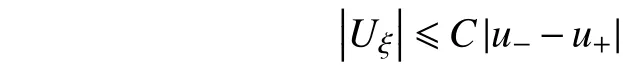
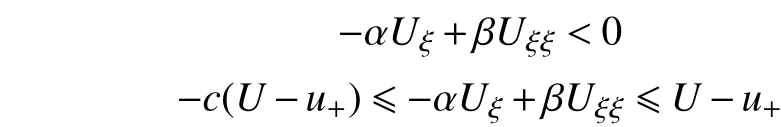
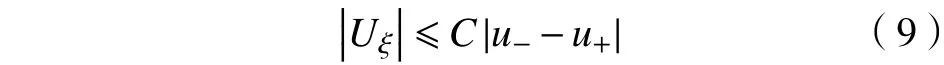
同理，利用微分中值定理以及式（9），可得

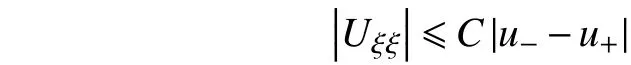
故性质3得证。

3 单调递减扭状孤波解的渐近稳定性定理

考虑方程（1）的初值问题，初值条件为

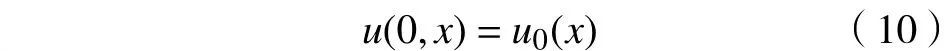
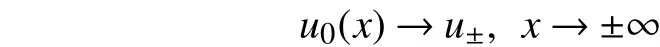
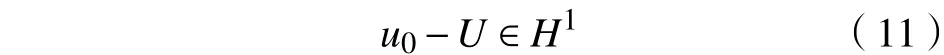
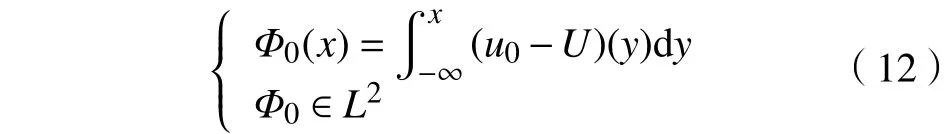
由条件式（11）和式（12）可知，

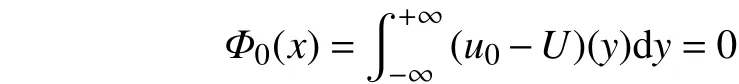
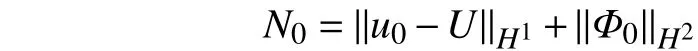
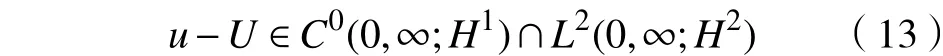
进一步，该解以最大范数的形式趋近于行波解

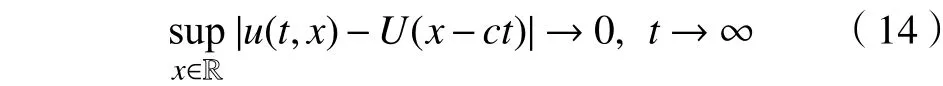
定理1的证明可以分为两部分：第一部分是证明解的整体存在性；第二部分则是证明解的渐近稳定性。

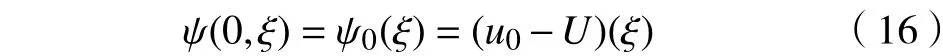
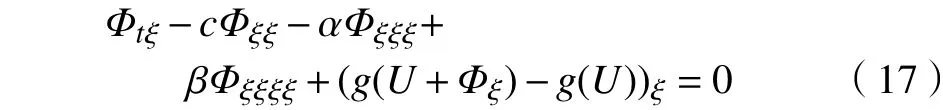
将式（18）线性化，则式（18）化为

其中，

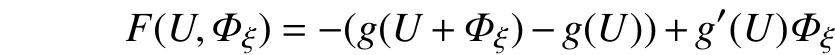
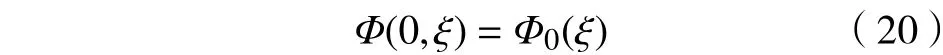
定义初值问题式（18）和式（20）的解空间为

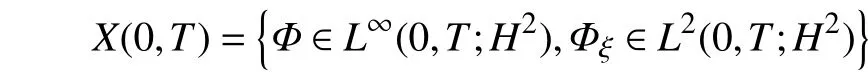
于是，有定理2。

对于定理2的证明也可以分为两个部分：第一部分证明初值问题式（18）和式（20）解的局部存在性；第二部分证明解的全局存在性。对于初值问题式（18）和式（20）解的局部存在性的证明，可运用Galerkin方法按标准方式进行证明，可参考文献[12-13]等。本文省略证明而给出定理3。

对于定理2中的初值问题式（18）和式（20）的全局存在性及不等式（21），需要在局部解存在的基础上给出一致先验估计。

引理2（Young不等式[14]） a. 令，，且，，则有下列不等式成立：

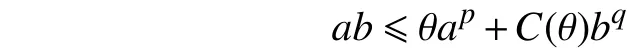
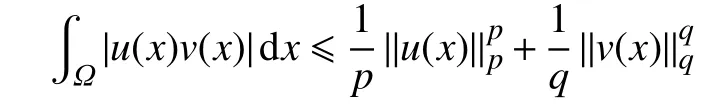
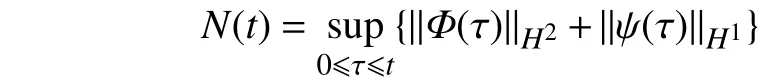
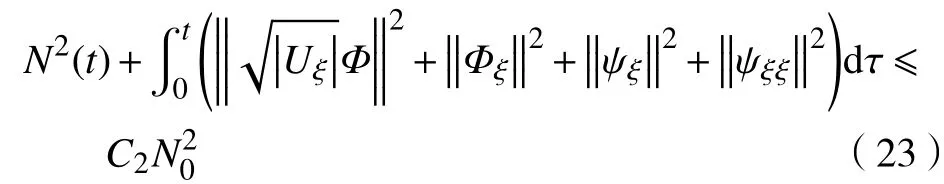
a. 低阶先验估计。

由于

故式（24）可写为

其中，

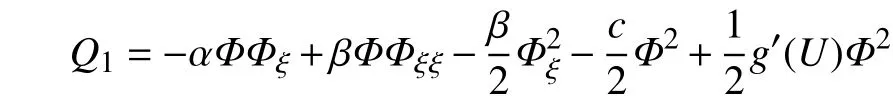
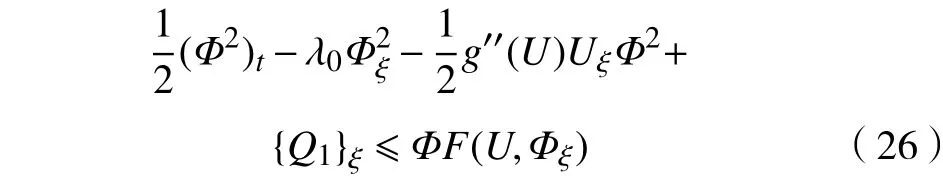
即

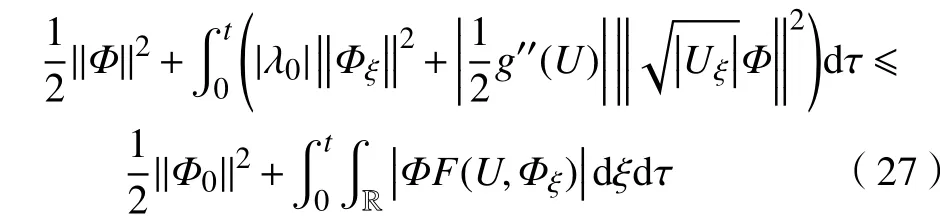
b. 高阶先验估计。

将式（15）线性化，有

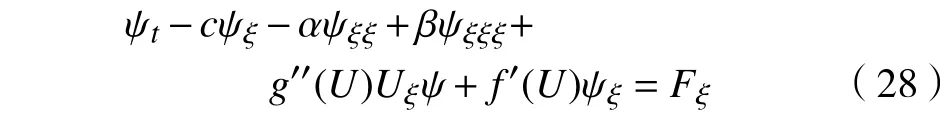
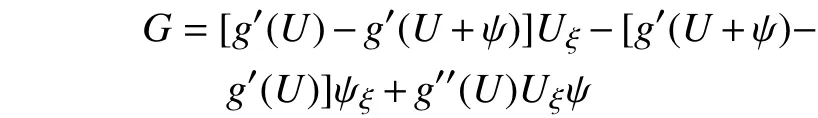
类似于对式（24）的分析，则式（29）可改写为

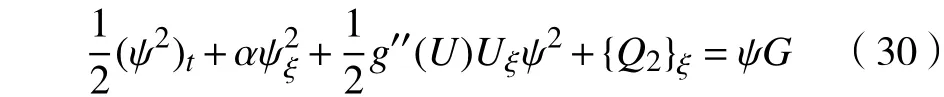
其中，

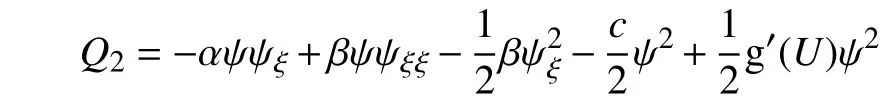
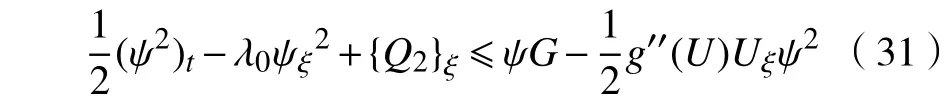
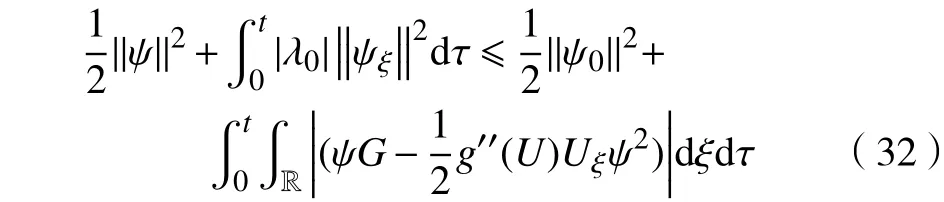
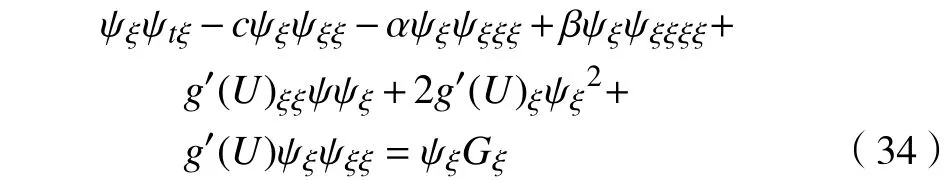
同理，类似于对式（24）的分析，则式（34）可改写为

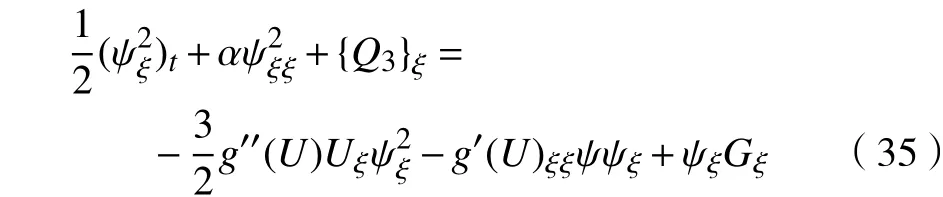
其

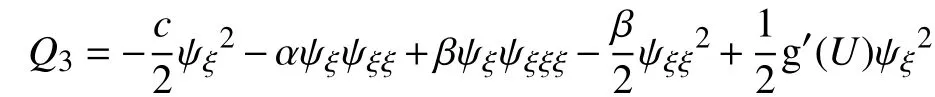
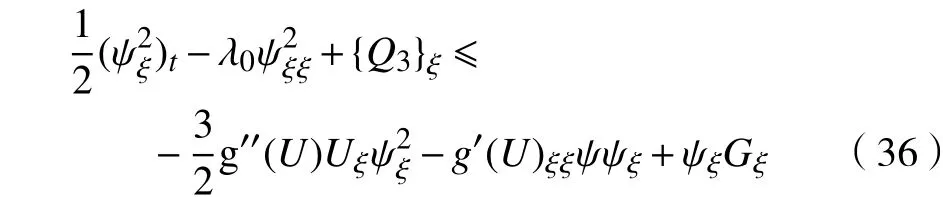
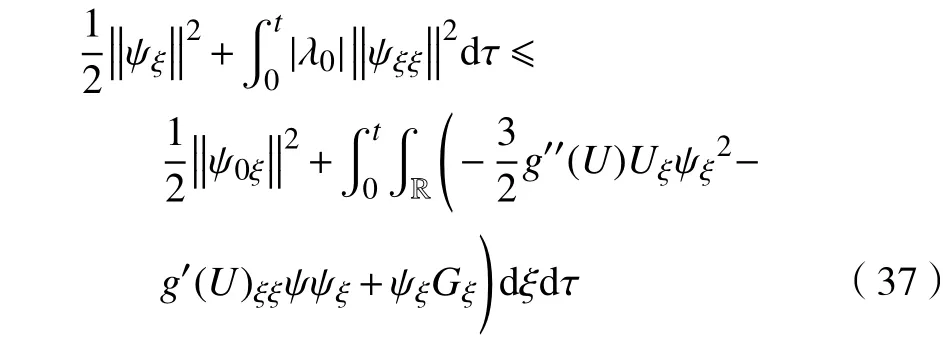
再将式（27），式（32），式（37）这 3式相加，有

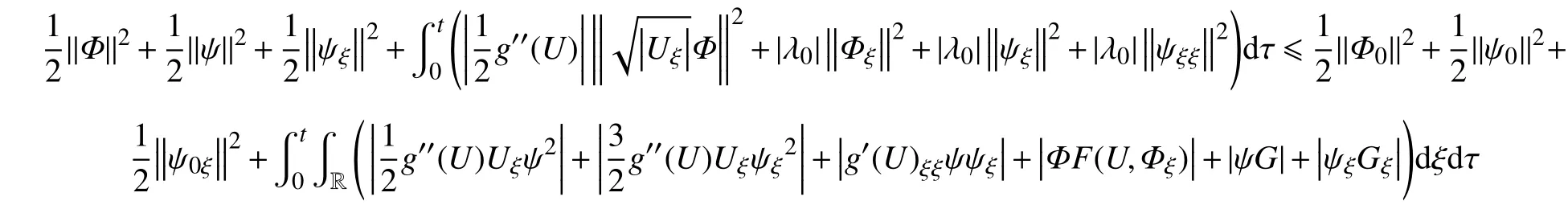
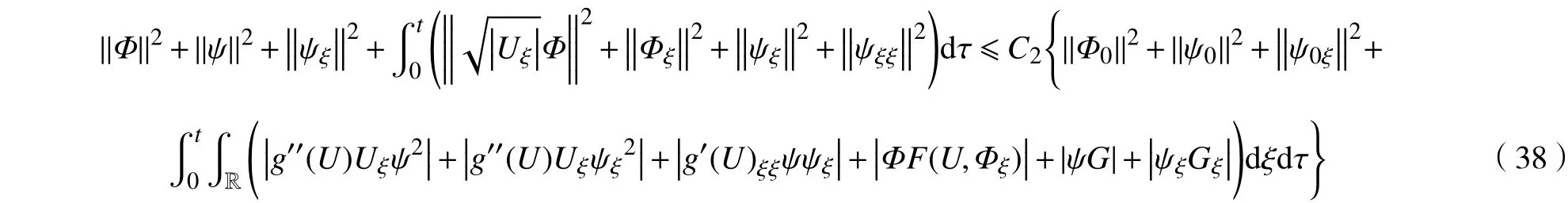
注意到式（38）右端第4项，利用Young不等式，有

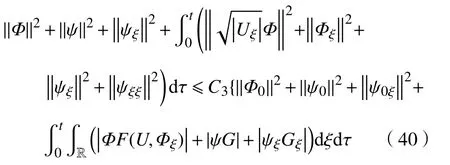
又因为，

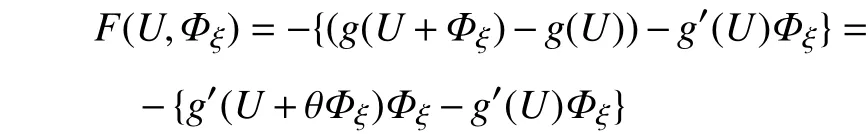
所以，

利用Young不等式，可得

即

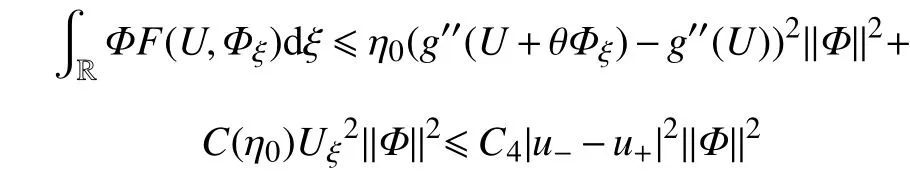
同样，利用Young不等式，可得

所以，

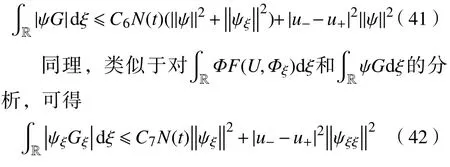
从而

由于在局部存在的时间区间内，式（22）成立，可得

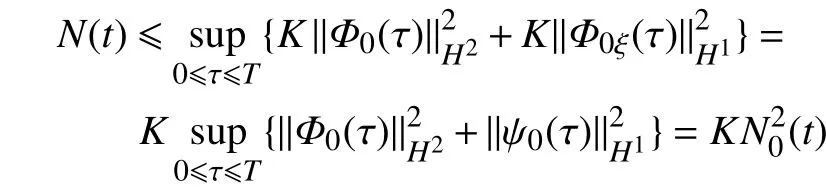
由此可知：

据（a）和（b）可以推知

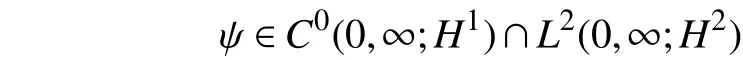
即

故式（13）得证。

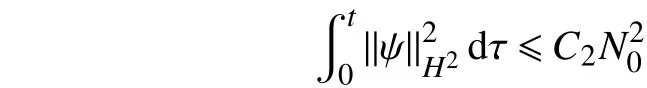
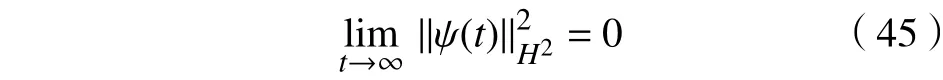
根据不等式[15]

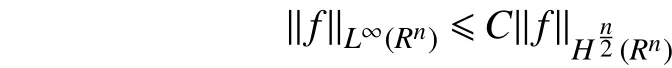
可得

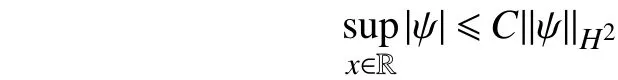
由此，根据式（45）即可推得

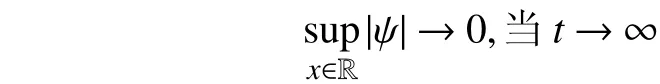
故定理1得证。

4 方程（1）单调递减扭状孤波解扰动的衰减估计

引理 3（Gagliardo-Nirenberg 不等式[16]） 假设，，，，则对任意，有

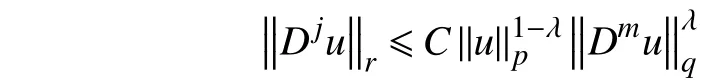
其中，

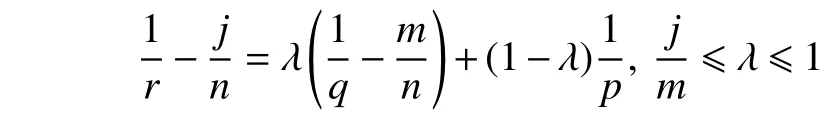
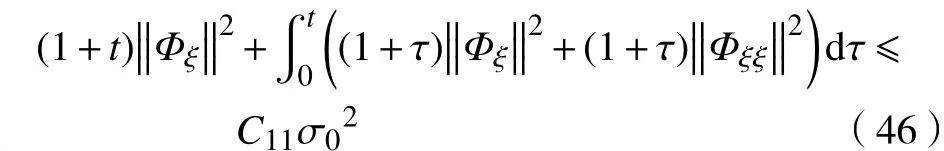
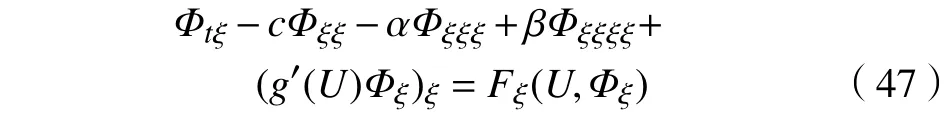
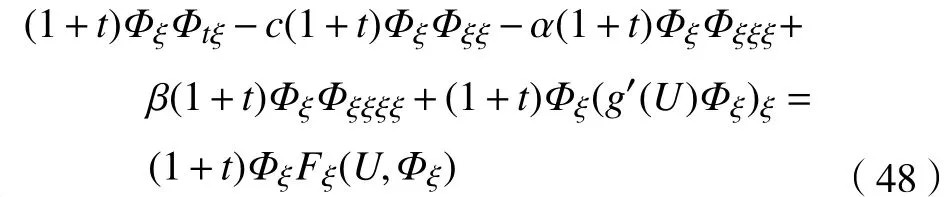
由于

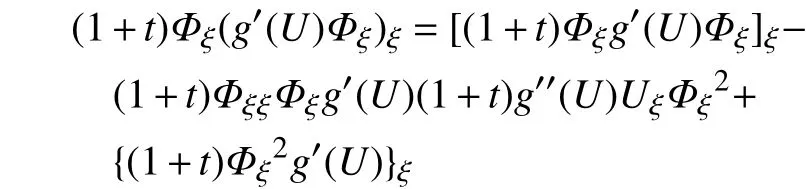
故式（48）可写为

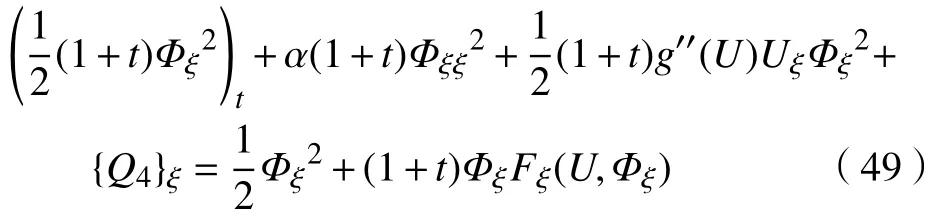
其中，

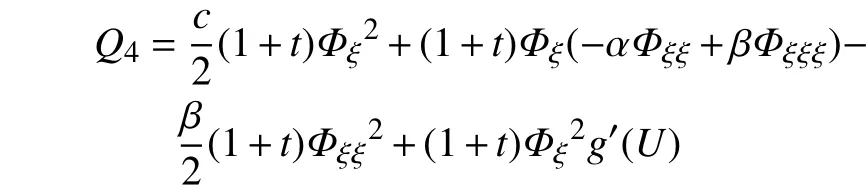
又由式（49）左边第2项，有

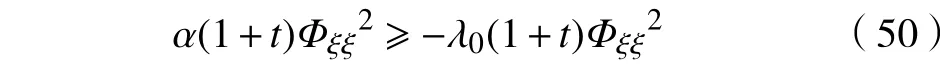
将式（50）代入式（49）中，有

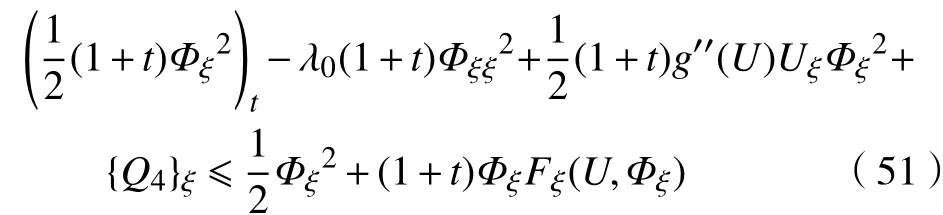
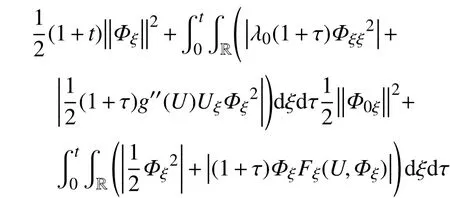
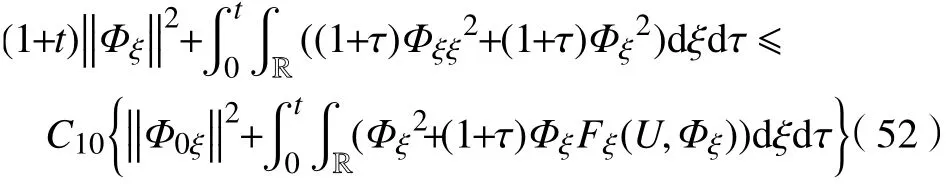
又由式（23）可知

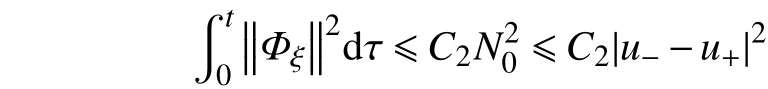
注意到式（52）中，

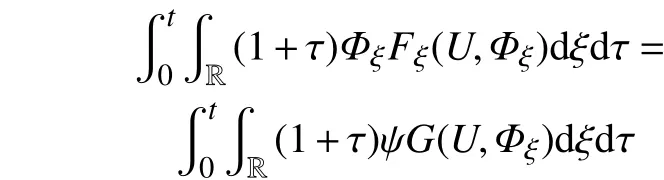
类似于对式（41）与式（43）的分析，有

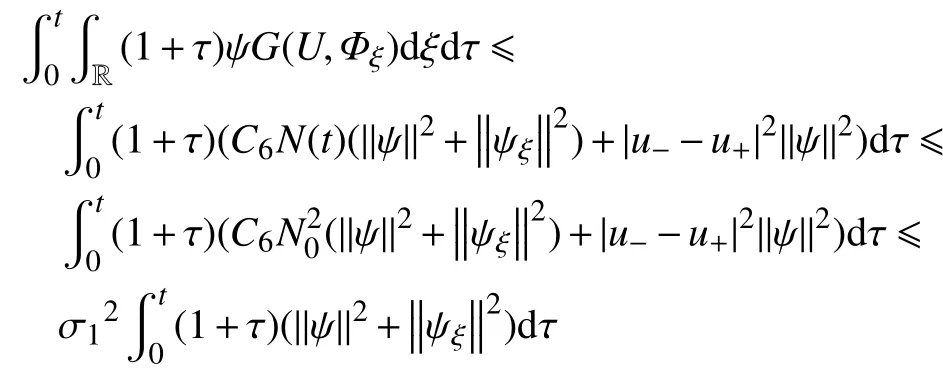
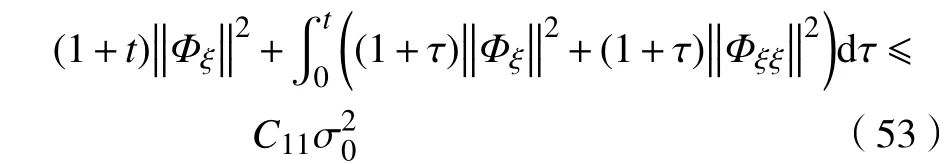
故定理4得证。

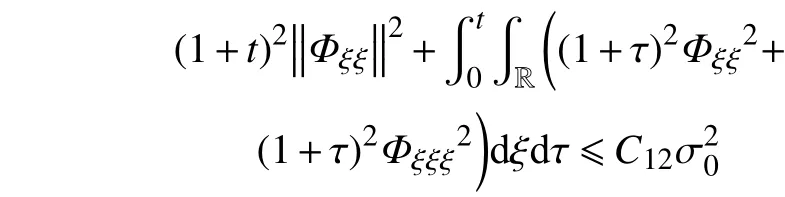
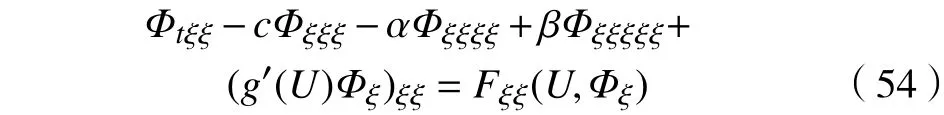
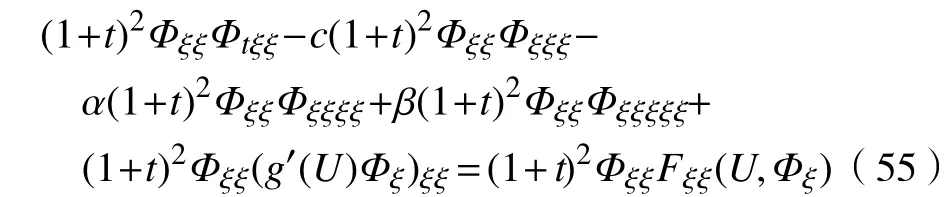
类似于对式（48）的分析，式（55）可改写为

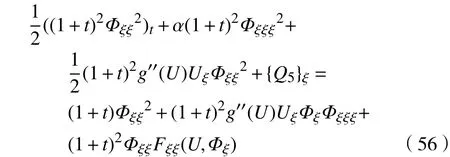
其中，

又由式（56）左边第2项，有

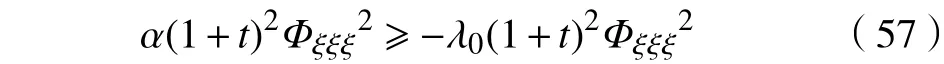
将式（57）代入式（56）中，有

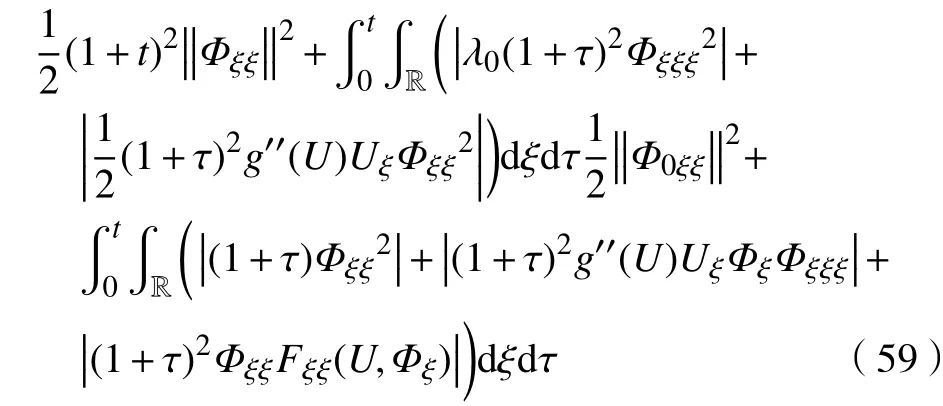
由式（53）可知

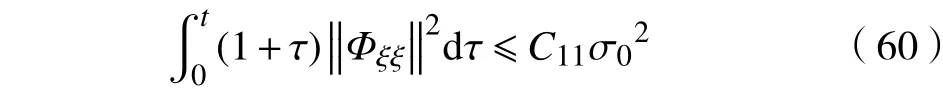
注意到不等式（59）右端第3项，运用Young不等式，

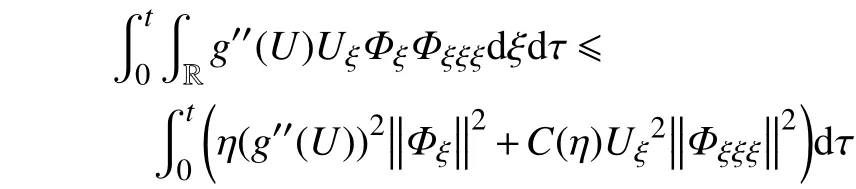
从而，

又

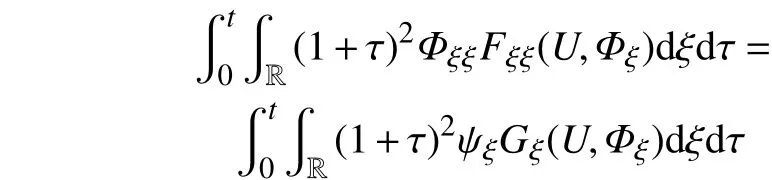
根据式（42），有

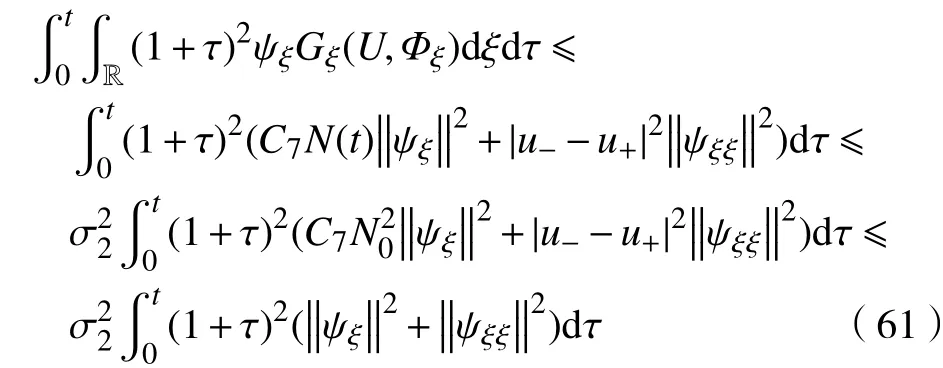
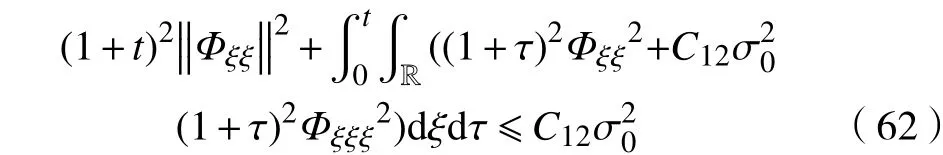
故定理5得证。

由式（53）可知

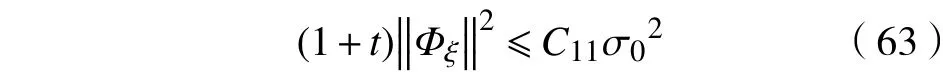
又由式（61），有

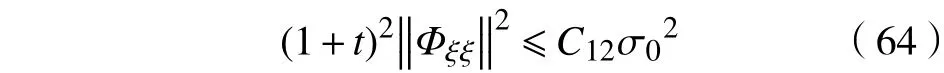
由式（62）和式（63），有

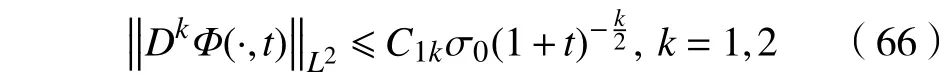
再由Gargliado-Nirenberg不等式，得到在范数意义下的衰减速度为

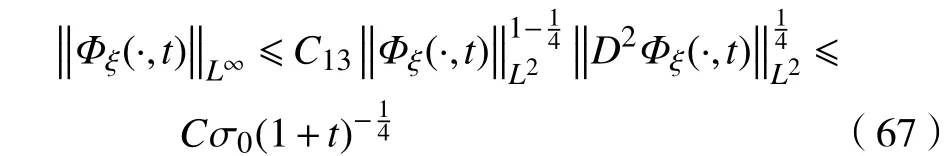
5 结 论

b. 组合KdV-Burgers方程（1）单调递减扭状孤波解的扰动在与范数意义下的衰减速率分别为和。