稳健经验似然估计方法

苏依官， 樊亚莉， 徐孝琳

（上海理工大学 理学院，上海 200093）

普通最小二乘（OLS）估计和最大似然（ML）估计是线性回归模型[1]中常用的参数估计方法。这些方法在分布假设合理的情况下表现良好，但是，当实际的数据不一定满足这些假设的情况下，这些方法所得到的估计会有较大偏差，这时需要考虑其他非参数估计方法。经验似然（EL）方法就是一种非参数推断方法，它是由Owen于1988年在完全样本下提出的一种统计推断方法[2]，它有类似于boot-strap方法的抽样特性。这一方法与经典的统计方法相比优点突出，当用经验似然方法构造置性区间时，它具有域保持性、变换不变性、Bartlett纠偏性等诸多优点。同时，经验似然置信域的形状只由样本决定，无需构造枢轴统计量[2-3]。正因为如此，经验似然统计方法引起了许多学者的重视，他们将这一方法应用到各种统计模型及统计推断问题中，如总体均值的估计、线性回归模型的拟合、分位数的估计[4]、估计方程[5]的建立，同时它也可以在不完全的删失数据[3]中得到很好的应用。实际上，EL方法的本质是带约束的最优化问题，在经验似然方法中，对每个观测值赋于一个权重，EL估计就是最大化权重乘积，而人们感兴趣的参数一般体现在该最大化问题的约束条件中。

众所周知，OLS，ML估计方程对异常值较为敏感，当数据中存在异常值时，用普通的OLS和ML估计方法所得估计会有较大的偏差和方差，而稳健的估计方法恰好可以弥补这一点，有许多学者讨论了稳健估计的重要性以及如何构造稳健估计量[6-10]。它可以在异常值存在的情况下，选择适当的抑制异常值影响的技术，使参数估值尽可能不受其影响，得出正常模式下的最优或接近最优的参数估值。由于EL方法目标函数的约束条件继承了OLS估计方程的原理，而异常值的存在也可能对EL估计产生较大的影响，因此，如何改进EL方法约束条件中的估计方程使之能够有效抑制异常值的影响，这是一个值得研究的问题。文献[11]考虑将稳健估计方程和经验似然方法结合起来，构造稳健的经验似然估计，但是，他们的估计方程只考虑了限制因变量中的异常值，对自变量中可能存在的异常值并没有采取相应的措施。

本文考虑稳健的经验似然估计方法，基于经验似然方法，在约束条件的估计方程中用一个依赖于自变量的权重函数使得杠杆点对估计方程的影响降低，并且对残差项使用一个有界的得分函数来限制因变量中异常点的影响，从而在数据分布来源未知的情况下有效地抑制可能的异常值对估计的影响。

1 模型和方法

1.1 普通经验似然估计方法

考虑一般线性模型

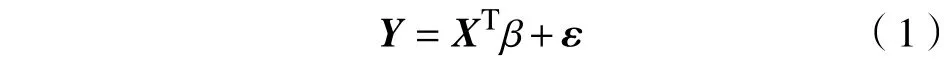
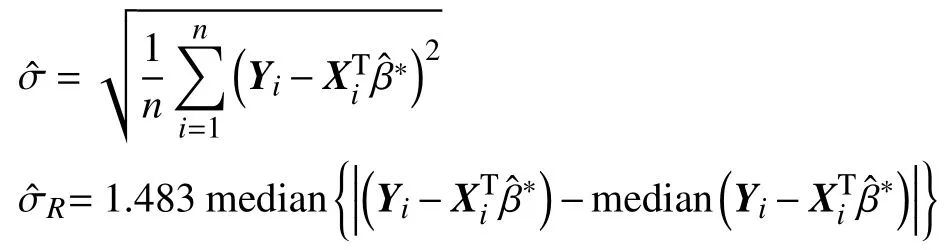
对线性模型（1），EL估计是下面优化问题的最优解[4,12]。

最大化目标函数

其约束条件为

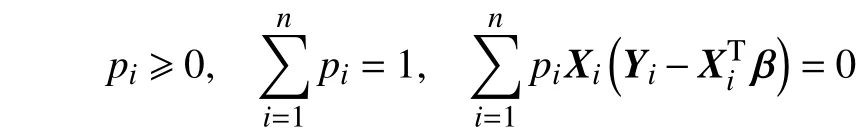
记

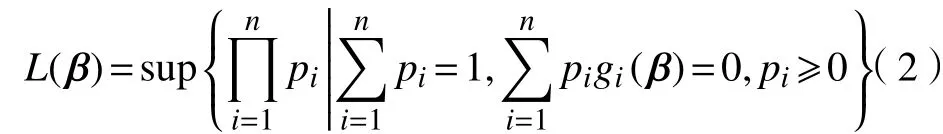
1.2 稳健的经验似然估计方法

考虑到实际数据受各种因素的影响，会有不同程度的污染，若仅按式（2）估计，势必会有较大的偏差。于是，在经验似然估计的基础上进行稳健化处理[13-14]，即稳健的经验似然估计。

a. 定义有界得分函数

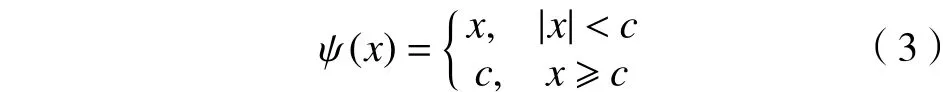
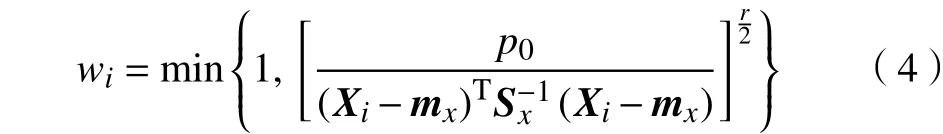
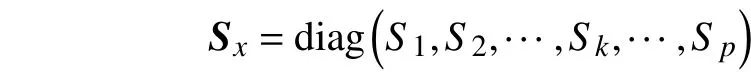
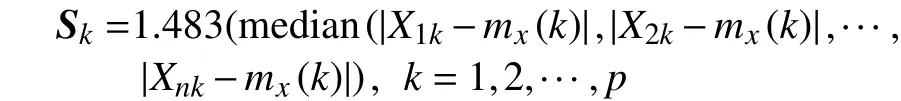
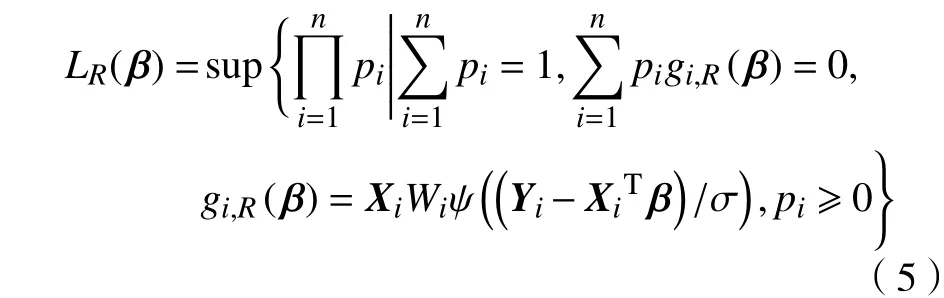
2 理论性质

现针对提出的稳健经验似然估计解的存在性以及估计量、统计量的性质给出一些理论证明，证明方法类似于文献[4]。记，，定义

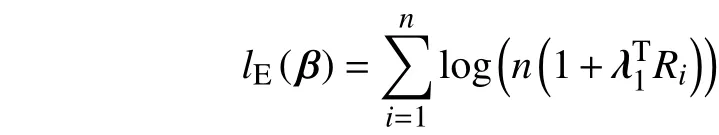
显然，上式的最小值点为式（5）的解[15]。

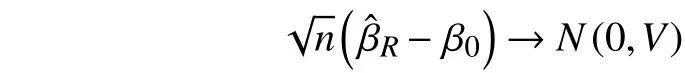
这里

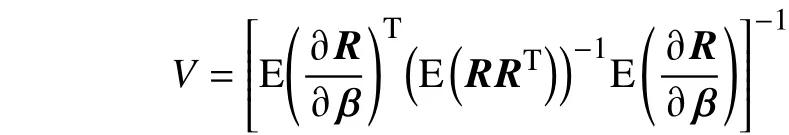
3 算 法

3.1 普通经验似然估计求解

式（2）的解等价于如下目标函数的解[16]：

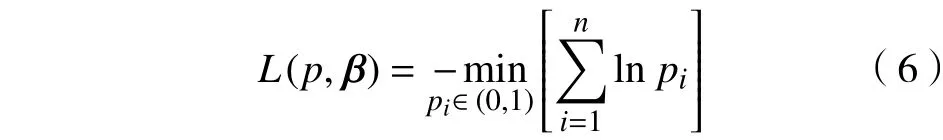
对于一般的带约束的函数求极值普遍采用拉格朗日乘数法，得到下式：

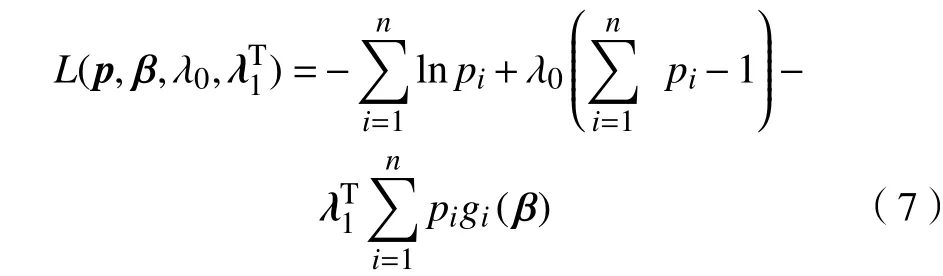
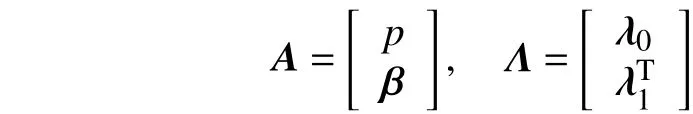
式（7）的一阶梯度为

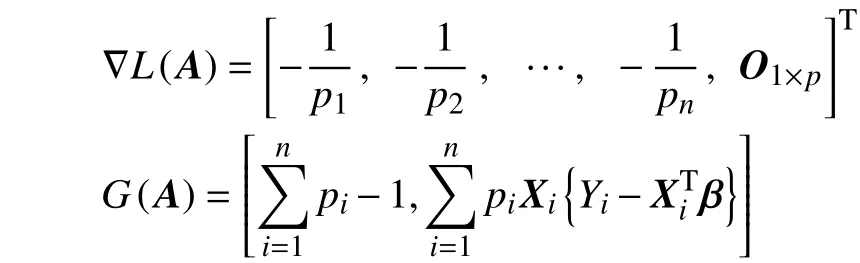
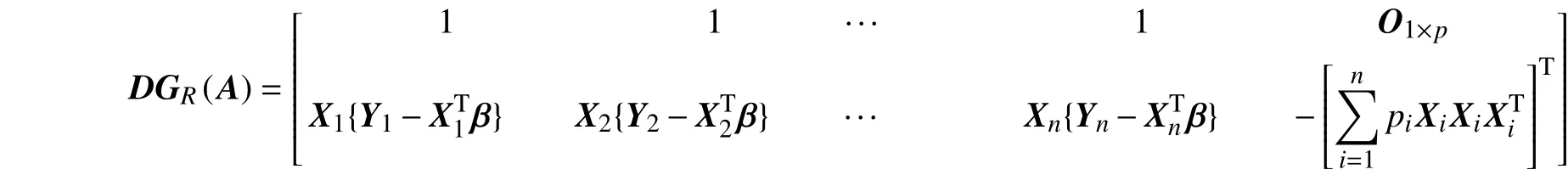
那么，式（7）的Hessian矩阵可表示为

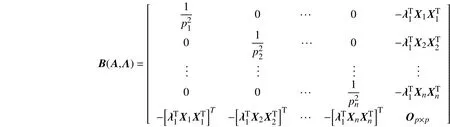
根据牛顿迭代原理，可以得到

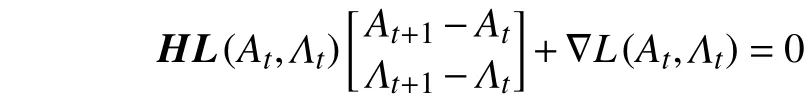
该算法的步骤可以归结如下：

3.2 稳健的经验似然估计求解

由于稳健方法与非稳健方法的区别只在估计方程中，因此，算法类似，只是将和变成和。其拉格朗日函数为

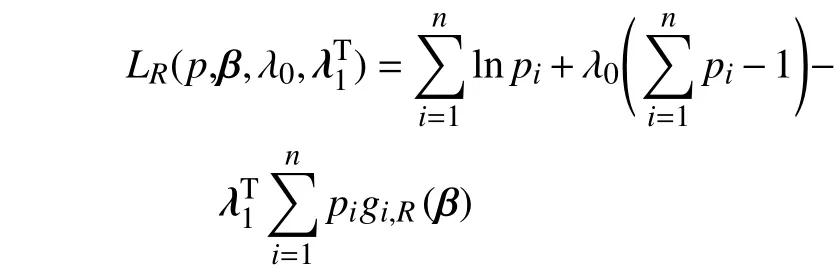
新的迭代式为

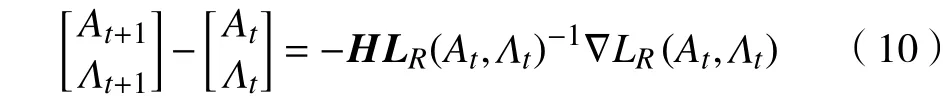
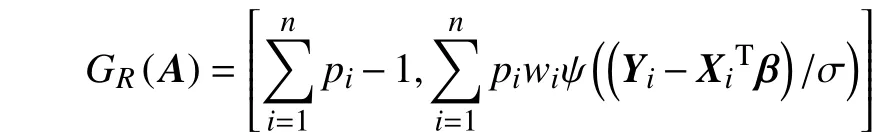
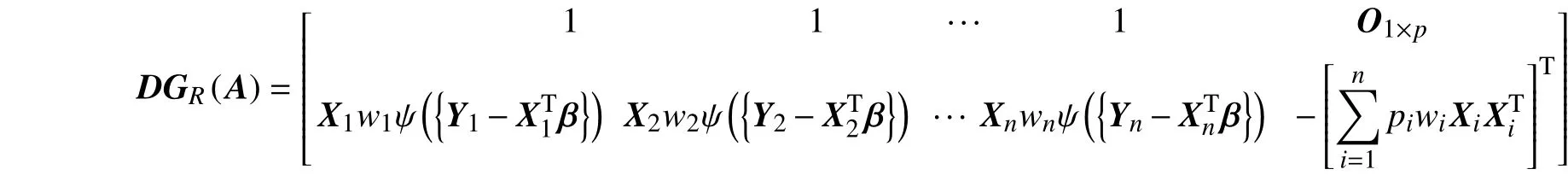
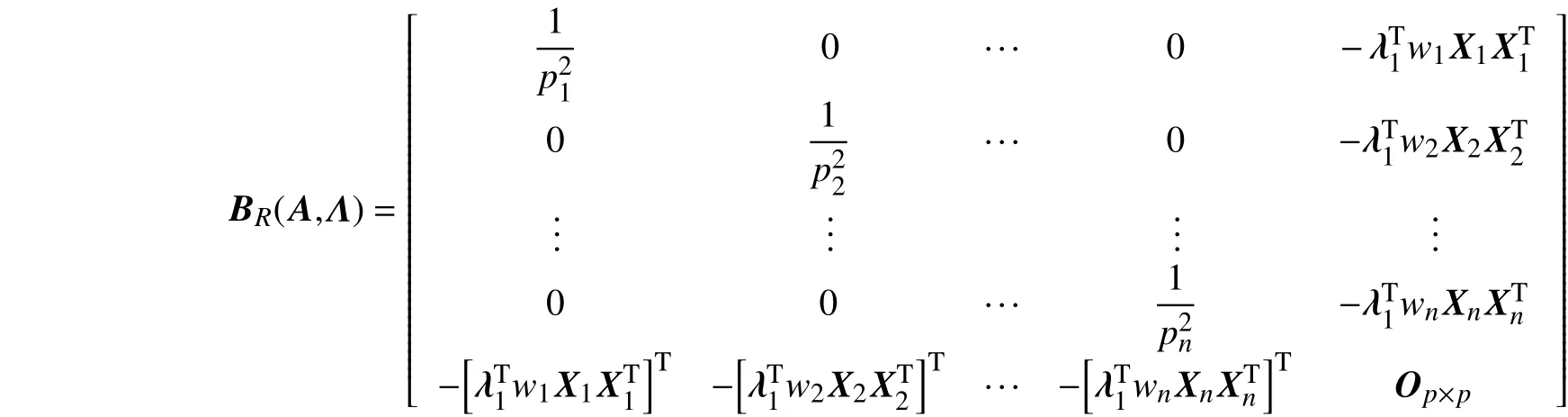
4 模拟研究

为了研究稳健经验似然估计方法在有限样本下的表现效果，通过模拟试验将稳健方法与非稳健方法以及最小二乘方法进行比较。

4.1 数据的产生

试验1 对于一般的参数估计方法，误差项往往取自标准正态分布，为了说明本文所述方法同样适用，在试验1中取自。

试验2 考虑到本文的估计方法是一个非参数方法，不同于参数的方法，其对误差项分布来源没有太严格的要求，为了验证这一点，在试验2中取 自。

4.2 数据污染与方式

为了考察本文的稳健方法的优势，对于试验1通过几种污染数据的方式产生数据中的异常值。

污染3 污染1，污染2同时进行。

4.3 结果与分析

在表1中，NR表示在无污染下的非稳健方法，R表示在无污染下的稳健方法，NR-C1表示在污染1下的非稳健方法，R-C1表示在污染1下的稳健方法；在表2中，OSL-t（1）表示在残差项服从t（1）厚尾分布下的最小二乘法方法，其余符号的含义类似。记录下3个分量在各指标下的结果，每个指标下各设置1个综合量，利用3个结果的二范数来更直观地比较各种估计方法的优劣。

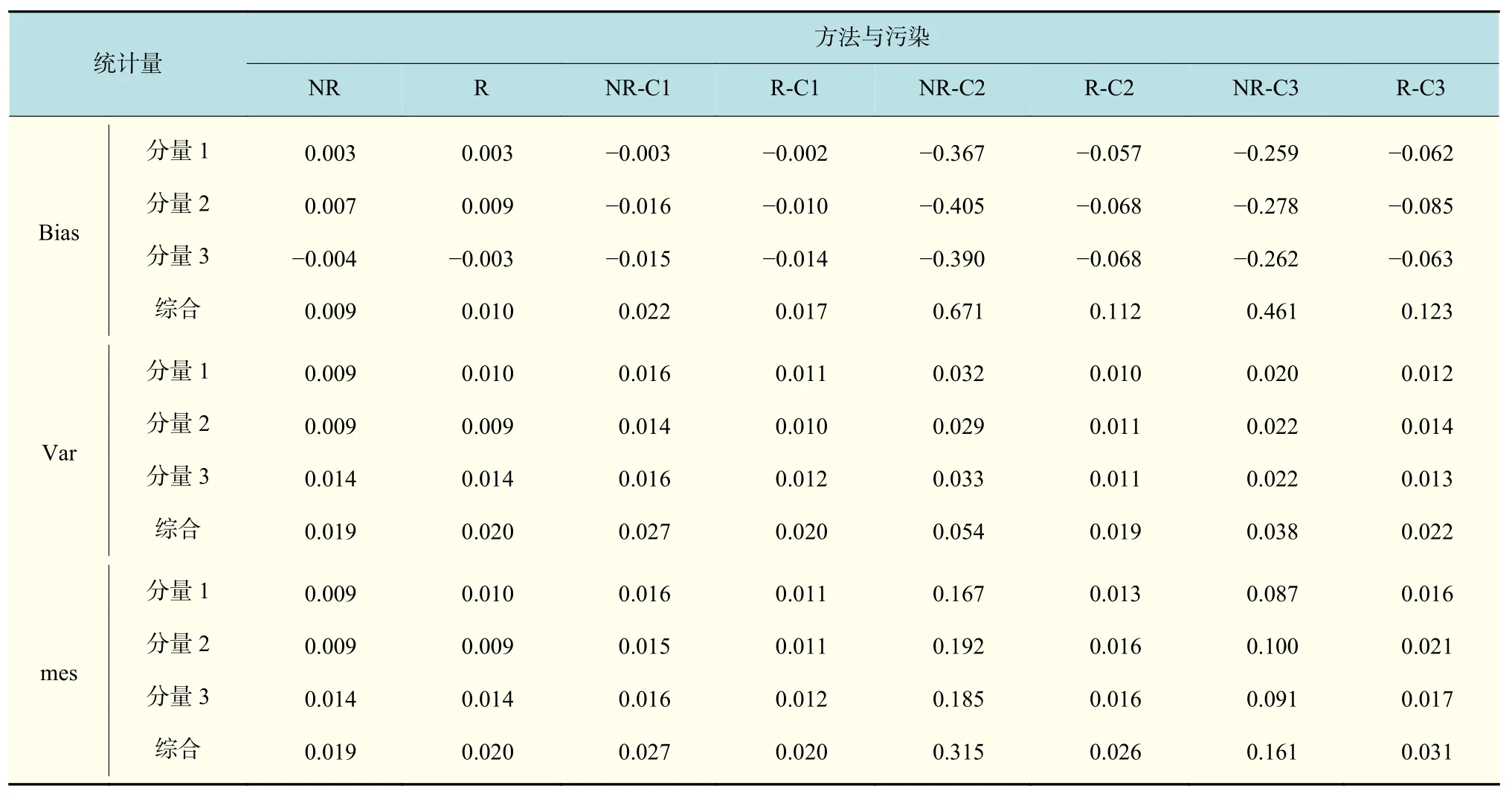
表 1 试验1的模拟结果Tab.1 Simulation results of experiment 1

结论：

a. 稳健与非稳健方法处理无污染数据的情况。对于误差项来自的情况，大体上稳健方法的3个指标的综合量略微大于非稳健方法的，因为，稳健方法损失了数据中的一些信息，这完全是正常的。对于误差项来自的情况，稳健方法的3个指标的综合量均大幅小于非稳健方法的，在表2中，，的偏差分别为0.777，0.061，方差分别为43.996，0.381，均方误差分别为44.402，0.384，说明稳健方法的优势尤为明显。

c. 从方差角度观察，污染1（仅对X污染的情况），以及误差项来自的情况，稳健的方法的该指标各个分量基本都小于非稳健方法的。而对于污染2、污染3（即包含对的污染），大体上稳健方法的该指标各个分量基本只是略微大于非稳健方法的，说明该稳健方法在受污染时对方差的控制也比较稳定。

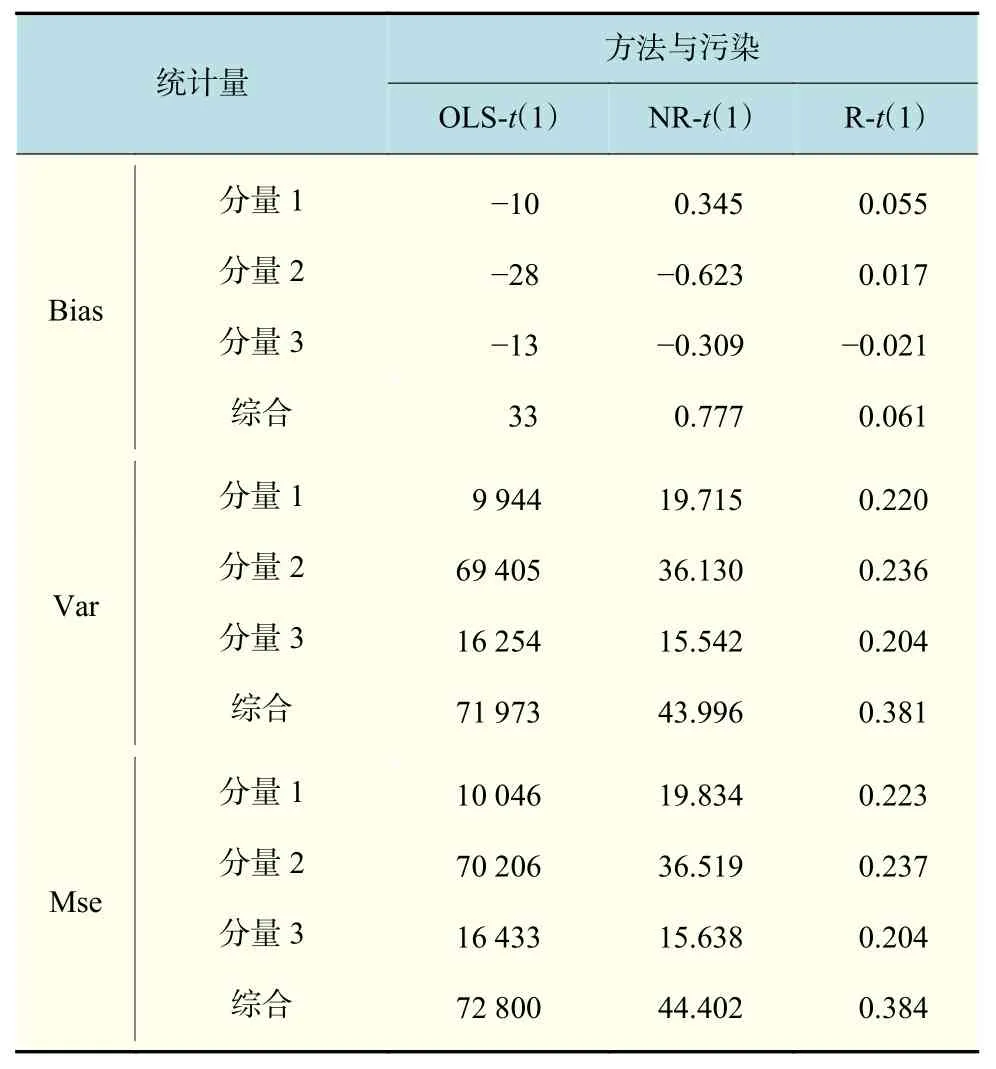
表 2 试验2的模拟结果Tab.2 Simulation results of experiment 2

5 实证分析

将本文提出的稳健经验似然估计方法应用到全国各地区房价预测中，这批数据共收集了35个地区在2014年的住宅商品房平均销售价格及在岗职工平均工资、生产总值、住宅房屋竣工面积3个可能的影响因素数据。其数据来源于国家统计局及各城市的统计年鉴http：//www.stats.gov.cn/。

将每个地区看作一次观测，每次观测有4个数据，将观测到的住宅商品房平均销售价格作为因变量，将剩下的3个观测指标作为基本自变量，在此基础上添加3个自变量平方项、交叉项作为生成自变量。对于交叉项，经实际数据的回归分析只取在岗职工平均工资与生产总值乘积项。

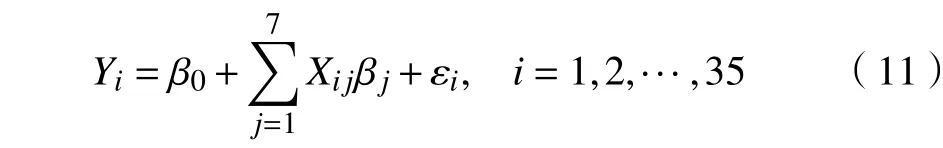
考虑到实际数据各项指标单位不同，数值差异较大，因此，先将各项指标标准化，使其均值为0，方差为1。现将本文的稳健经验似然估计方法与非稳健经验似然方法应用到这批数据中。为了考察本文方法的稳健性，进一步用交叉验证方法比较稳健与非稳健方法的两种表现，每次剔除1个地区数据，用剩下34个地区数据估计式（11）中的回归系数，并用CV来衡量两种方法在交叉验证过程的稳健性，定义

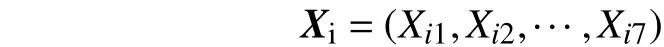
在表3中，NR为普通经验似然估计，R为稳健经验似然估计，VNR为普通经验似然估计的方差，VR为稳健经验似然估计的方差。从表3数据可以看出，稳健经验似然估计在稳定性方面优于普通经验似然估计，这一点可以通过对比VNR与VR在各系数下的值来得到。

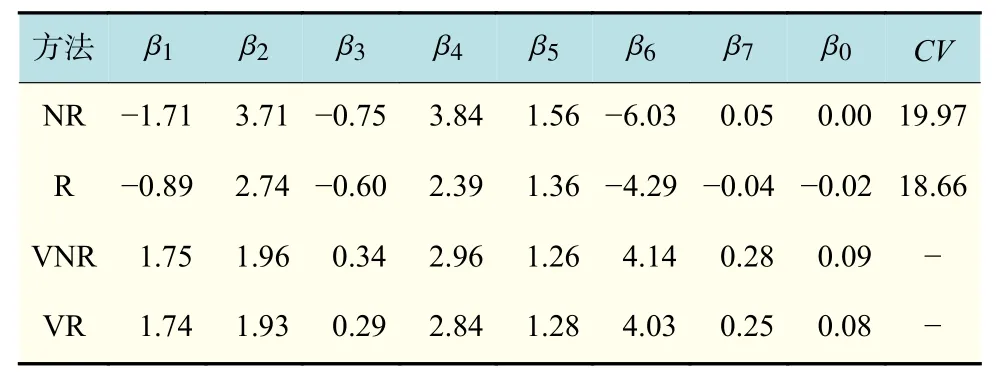
表 3 稳健与非稳健方法对房价数据的结果分析Tab.3 Analysis results on the price data by the robust and unsteady methods

观察前3个比较直观的变量，分别为在岗职工平均工资、生产总值、住宅房屋竣工面积。从经济学角度来说，供给和需求是决定商品价格的2个方面。住宅房屋竣工面积是通过供给方面来影响房价的。从经济意义上讲，住宅房屋竣工面积越多，说明对商品房的供给越多，房价的增长速度应该放缓，直至下降。因此，的理论值应是负的，本文的估计结果与之相符。在岗职工平均工资、生产总值是通过需求方面来影响房价的。人均可支配收入决定个人消费水平的高低，随着收入水平的提高，消费能力也会相应提高，增加的居民可支配收入会提高房屋的销售价格。收入的上涨可以收缩买房时间，这直接影响房地产的销售量和销售额。人均可支配收入较高的城市，其居民有相对充足的资金购房，其房价自然较高；反之，若房价相同，人均可支配收入较低城市的居民没有足够的资金购房，房价无疑会下降。因此，的理论值应是正的，由于受到部分地区的异常值影响，导致经验似然估计结果较差，为-1.71，而本文的稳健方法可以较大程度地减小这种影响，其估计结果为-0.89。房价是商品价格的体现，当生产总值增长时，房价也会随之增长。日本在1991年之前长时间的经济增长与房地产泡沫可以体现这点。美国的经济飞速增长，房价也随之增长。反之，如我国东三省因为依赖的重工业发展缓慢，导致生产总值增长缓慢，人口外流，从而间接导致房价下降。因此，的理论值应是正的。

CV值越小，表示该方法稳健效果越好。计算非稳健方法的CV值为19.97，稳健方法的CV值为18.66，小于前者，因此，稳健方法得到的结果比较稳定，同时也说明了数据中存在某些异常值。实际上，杭州、北京、深圳等几个城市的房价确实存在过高现象，这与本文的分析结果相符。

6 总结与展望

基于稳健估计方程和经验似然方法，提出稳健经验似然估计，研究了相应的算法，并作了大量模拟研究。研究表明，当数据中不含异常值时，稳健经验似然估计的效果和普通的经验似然估计的效果是相近的，但是，当数据中含有异常值时，稳健经验似然估计的效率明显高于普通的经验似然估计的效率。随着污染力度和污染比例的增加，稳健经验似然估计方法的优势更为明显。同时，模拟表明，作为一种非参数估计方法，本文的稳健经验似然估计适用于分析非正态的数据。因此，对于实际生活中的数据分析，建议使用稳健经验似然估计。

在本文研究的基础上，进一步还可以考虑将稳健经验似然估计方法运用到纵向数据分析中，同时还可以考虑在稳健估计的基础上作变量选择等，这些问题都值得进一步研究。