无言的结局

张小渔

(江苏省苏州国际外语学校 215000)

代数题，在求解时有的比较繁琐、有的比较困难.如果我们换一种思路，通过挖掘其隐含的几何背景，构造出符合题意的几何图形，解答往往极其简单、直观.请看以下几例.

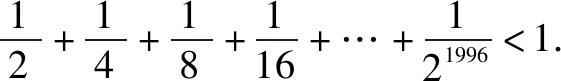
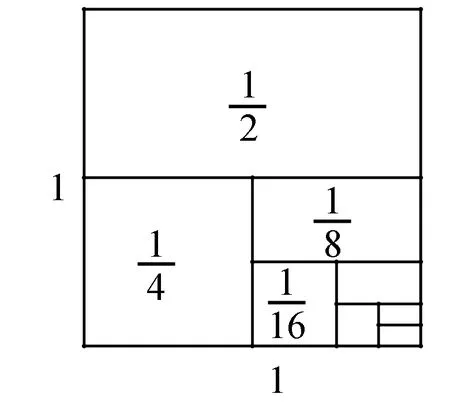
图1

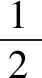
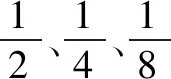
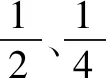
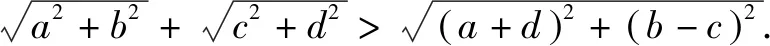
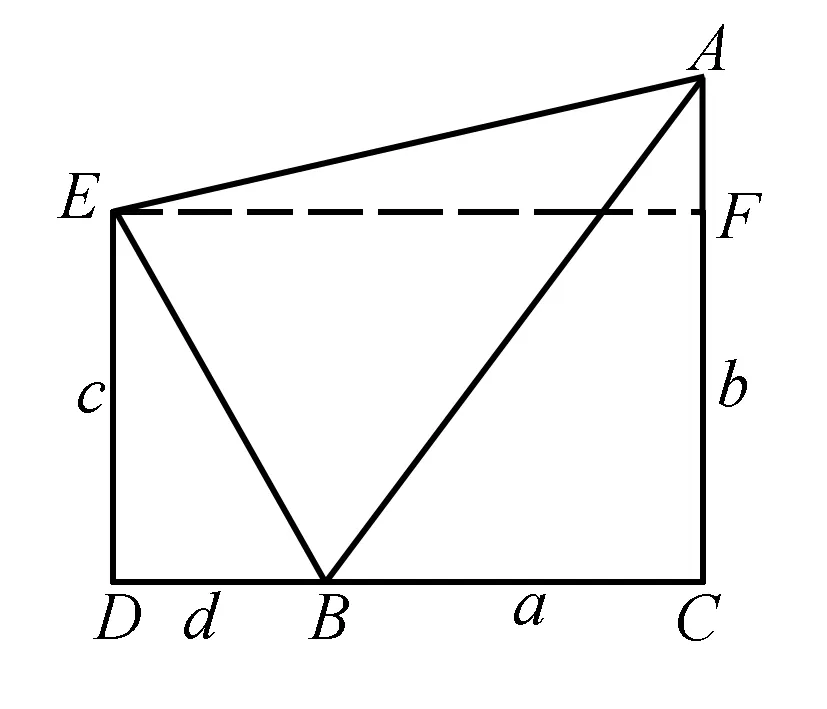
图2

分析本题从解不等式的角度，必须经过两次运算推理，繁琐是免不了的.若能把根式反映成直角三角形的斜边的长，本题的三个二次根式就转化为三角形三边长，也就不难求证了.

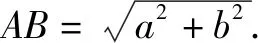
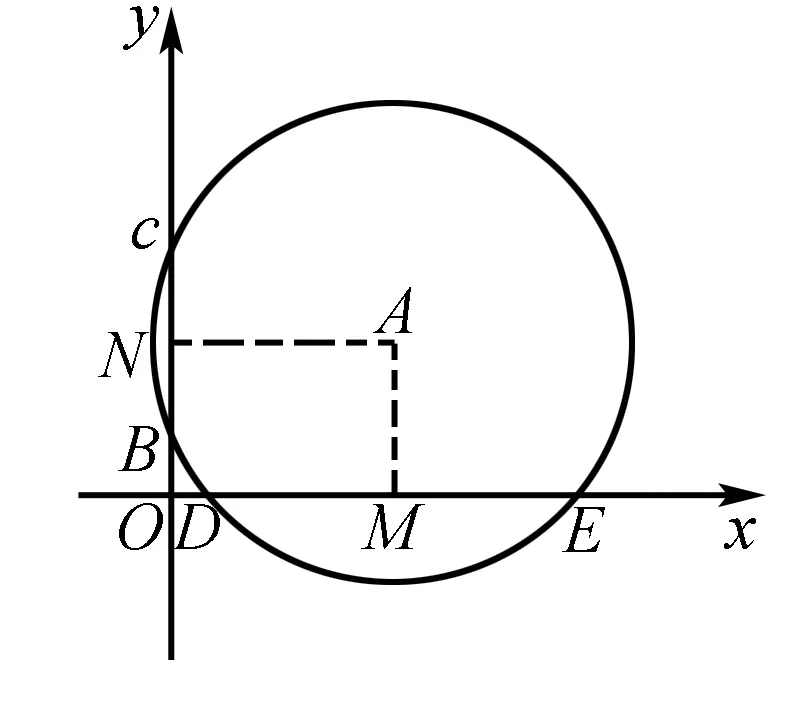
图3

例3已知方程x2-px+rs=0(p、r、s都是正实数)，且p2-4rs≥0，试用几何方法求方程的根.

分析要求方程的两根，由于两根之积为rs反映成几何图形就是圆中的切割线定理或相交弦定理，那么如何构造两根之和呢？如果借助两线段和及中点坐标公式问题就迎刃而解了.

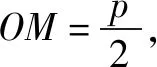
评注本题从一个全新的角度让我们认识一元二次方程的根，只要制作精度较高的直角坐标系，对于x2-px+rs=0的方程，当其中的p2-4rs≥0,且p>0,r>0,s>0，根据p、r、s的读数，也就相应得到方程两个根的近似值的读数.

本题的求解让我们学到如何处理两数和与积的构图方法.

著名的勾股定理的证明方法多达300余种，大多数是利用构造图形来证明的.下面我们一起欣赏一下美国第十二届总统加菲尔德的证明.

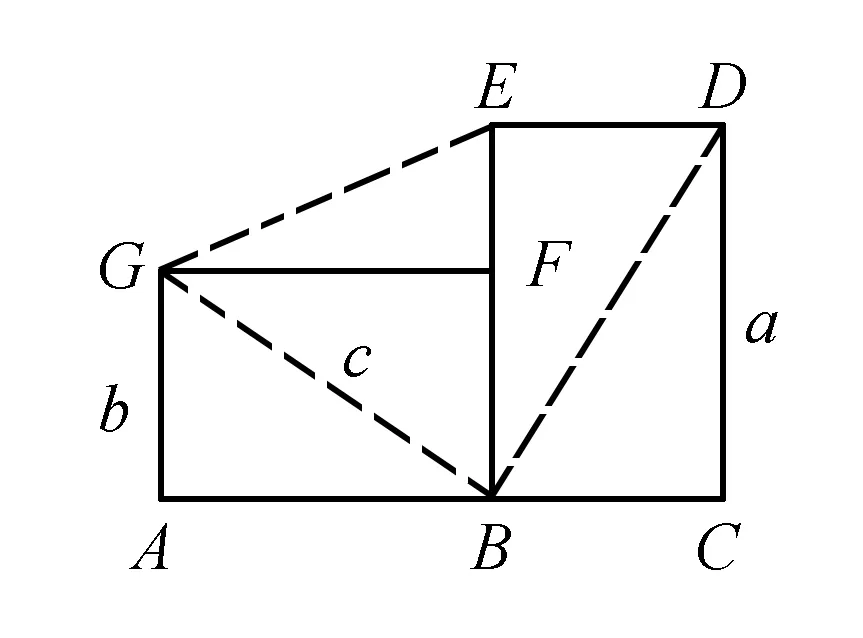
图4

例4如图4,构造两个全等的矩形显然有：

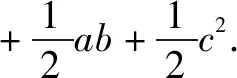
综合得a2+b2=c2.

人们戏称，美国总统踢倒一块砖头便证明了勾股定理.