基于协同进化算法的集中竞价市场模拟分析

2019-08-13陈皓勇尚金成刘雨梦

浙江电力 2019年7期

何洋，黄龙，陈皓勇，尚金成，李鹏，刘雨梦

（1.河南电力交易中心有限公司，郑州 450046；2.华南理工大学电力学院，广州 510640；3.国网河南省电力公司经济技术研究院，郑州 450052）

0 引言

当前我国电力市场改革正在逐步推进，各省市都在积极寻求电改的契机和实施方案，针对现行的市场规则、评估规则的优劣性包含多方面的考量。基于实验经济学的模拟仿真能在一定程度上反映竞价双方的博弈过程，目前国内外已广泛开展实验经济学理论的应用研究。

实验经济学是应用实验的方法，在有显性或隐性规则的社会背景下，研究人类相互作用的决策行为，它将经济活动参与人实证化。文献[1]引入实验经济学方法探讨了统一出清方式和按报价结算方式，结果表明后者并不能降低平均电价水平。文献[2]提出人-代理混合实验方法，对多种电力市场模式开展仿真实验。价值诱导理论是实验经济学的核心理论[3]，在实际的决策实验中，往往利用报酬等媒介来实施方案。但是，实验经济学往往需要进行大量的实验来获得满意的结果，参与者受外因、环境因素干扰较大，实验者与参与者不可避免地被各种场外因素所左右。

近年来，协同进化作为一类智能算法，由于计算速度较快、精确度、鲁棒性较优等特点[4-6]，在各个领域得到了广泛应用。文献[7]对协同进化算法的代表性研究进展给予了综述，总结了协同进化算法的机制和算法设计。文献[8]提出一种自适应协同进化蝙蝠算法，提高了进化效率和收敛精度。协同进化算法在电力系统中的应用，在较早之前就开展了研究。文献[9]基于协同进化算法求解配电网重构问题，一定程度上提升了配电网的经济运行。文献[10]采用协同策略对系统进行无功优化，具有良好的收敛性能。文献[11]讨论了计及网络约束的供需双方竞价的博弈模型，求解了市场的均衡。文件[12]对比了协同进化算法和遗传算法、退火算法在无功优化中的应用，指出前者收敛性能更好，求解速度更快。研究表明，相比于其他智能算法，协同进化机制的寻优精度更优，能够被进一步运用到电力市场仿真均衡的求解中。

目前的市场出清机制包括统一出清和PAB（按报价支付出清）两种。统一价格和PAB 竞价的实验分析通常采用实验经济学与多商品同时拍卖模型，文献[13]采用实验经济学的方法对比了PAB和统一价格出清，结果表明统一价格出清时发电商之间的竞争更为明显。文献[14]在PAB 竞价机制的基础上，采用最优概率随机匹配模式，验证了其能更好地激励市场成员按照真实成本报价。文献[15]构建了电力市场双层优化模型，说明了不同出清机制下电价波动范围和电价大小都不相同。文献[16]建立了PAB 机制下基于概率分布的连续策略伯川德模型，结果证实了市场份额大的发电商倾向于报高价，从而产生市场力。

集中竞价交易包含边际电价法和报价撮合法两种方式，购售双方在电力交易平台申报电量、电价等信息。文献[17]立足云南实际情况，研究PAB 出清机制下集中竞价交易规则，表明其有效防范了市场力的产生。文献[18]基于四川省电力市场特征，提出了复式竞价模式，扩大了市场空间的竞争性。广东省作为电力市场改革先行点之一，其月度集中竞价市场采取申报价差方式，文献[19]利用实验经济学的方法对广东省出清价格影响进行了分析，验证不同供需比的价格变化情况。文献[20]利用JADE（Java 智能体开发框架）电力市场仿真系统，针对广东月度集中竞价市场，定量评估出清价格及偏差考核机制对市场表现的影响。

因此，本文在现有电力市场均衡模型的基础上，构建了统一出清和撮合出清机制的竞价模型，模型以发电公司和售电公司（用户）的申报电量和申报电价为变量，市场目标为各主体利润最大化，通过模拟市场博弈过程得到最终市场成交情况，并对各主体的报价过程作了分析。

1 协同进化算法

生物界中，协同现象广泛存在于物种间的交互与合作，各物种间通过竞争、捕食、合作等方式进行博弈和生存，从而最终达到生态的平衡。区别于遗传算法，协同进化算法在传统寻优的基础上增加了各种群的信息交流和博弈，种群成员通过不断更新自身的信息，参与整个大环境下的寻优，最终实现均衡求解。作为一种智能算法，协同进化算法可以被应用到市场间成员的博弈，进而探求发用双方竞价过程的动态变化。基于协同进化算法的市场出清求解需要3 个步骤。

步骤2：对各种群实行遗传操作。假设进化进行到第K 代，对个体报量、报价信息依次执行交叉、变异操作，同时执行精英保留机制，避免上一代最优报价策略遗失。

基于协同进化算法的流程如图1 所示。

图1 协同进化算法流程

可以看出，协同进化算法将各种群间个体通过策略集形式联系起来，避免了传统遗传算法种群的孤立性，更有利于进化的多样性，算法寻优也更精准。每一代个体依托上一代最优策略集为报价环境进行市场出清，可以看做是市场成员在已知上一次竞价结果的情况下，进行下一轮的报量、报价，寻求自身效益最大化。

2 市场模型

2.1 发电商与用户

市场环境下，发用电双方参与竞争的主要目的是为了使自身利益最大化，对于发电方来说，存在发电成本，即电厂发电所耗费的生产成本。通常情况下，发电机组生产成本和发电量存在函数关系，以火电机组为例，可将机组动态成本分为固定成本和可变成本，固定成本以电网目标年运行过程中的容量投资年金为基础，可变成本包含燃料费、水电费等费用。考虑机组煤耗情况，出力的变动导致单位成本变化，因此成本函数为二次曲线。

发电商成本函数具有如下形式：

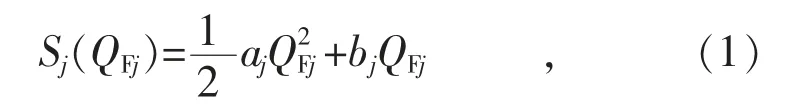
式中：QFj为发电商在市场中竞得电量；Sj为对应发电量的发电成本；aj，bj为发电成本系数。

对应发电商j 的边际成本函数为：

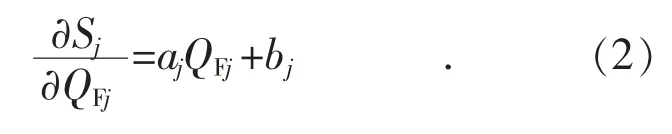
同理，对于用电侧来说，存在用户效益函数如下：

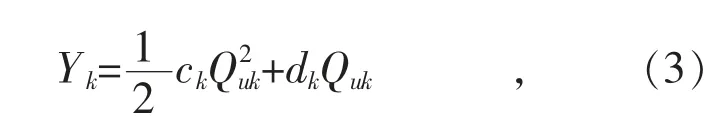
式中：Quk为用户在市场中竞得电量；Yk为对应电量的效益；ck，dk为效益函数的系数。

对应用户的边际效益函数为：

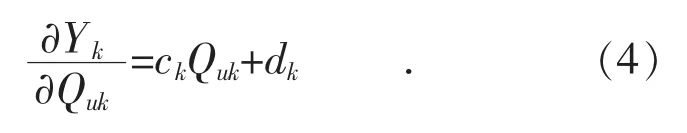
2.2 出清模型

假设市场上有j 个发电商和k 个购电商想要最大化其利润，依据月度集中竞价交易规则，市场假设如下：

（1）实际市场中，允许发电商和购电商进行n（n≤3）段电量申报，由于各段申报是相互独立的，因此可以看成由n 个发电商或购电商申报，仿真模拟中市场各主体只考虑单段申报。

（2）发、用电双侧均采用绝对价格申报电价、电量，计算所有可能的电力用户与发电企业的直接交易价差，交易价差大于等于0 则形成有效匹配对，由大到小依次撮合有效匹配对，申报价差对相同情况下，售电侧按照环保节能顺序优先，购电侧按照申报比例分摊电量。

（3）市场出清方式分为两种，一种是采用统一出清的模式，以最后一个撮合匹配对形成的价格作为市场的统一出清价格；另一种是按照报价撮合法，由各有效匹配对依照价差均分原则形成市场双方交易价格。

（4）各发电商的利润为售电收入和发电成本之差，各购电商的利润为需求效益和购电成本之差，决策规划目标如下：

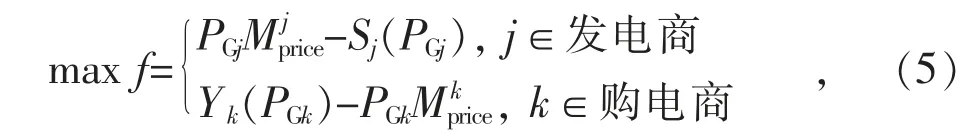
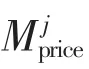
3 仿真分析

3.1 实验方案

本次实验的目的是研究月度集中竞价背景下，报价撮合出清和统一出清机制下发、用电双方的博弈情况，依据不同类型发电商和用户（售电商）竞价信息和成本函数，利用协同进化算法求解市场均衡，分析不同参与者的竞价行为。

实验设置4 个发电厂商和4 个用户（售电商），发电商和用户的申报电量和申报电价均为决策变量。其中，发电厂商和用户的电量申报上限均为1 000 MWh，上网标杆电价设定为0.355元/kWh，实验参与者根据上网标杆电价来申报价格。种群中个体数量为50，设定交叉因子为0.5，变异因子为0.15，市场各主体参数设置见表1 和表2。

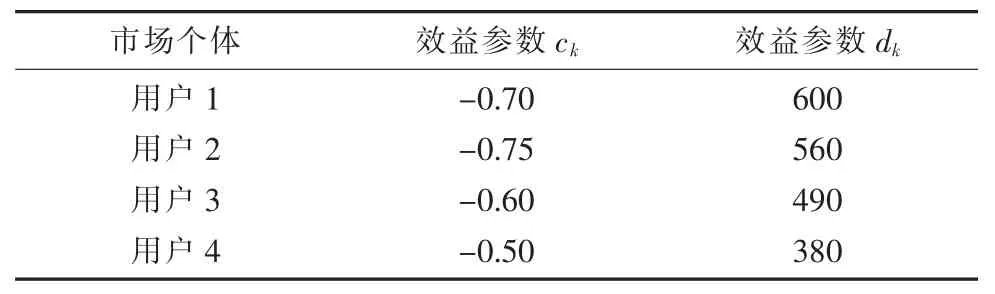
表1 用户参数设置情况

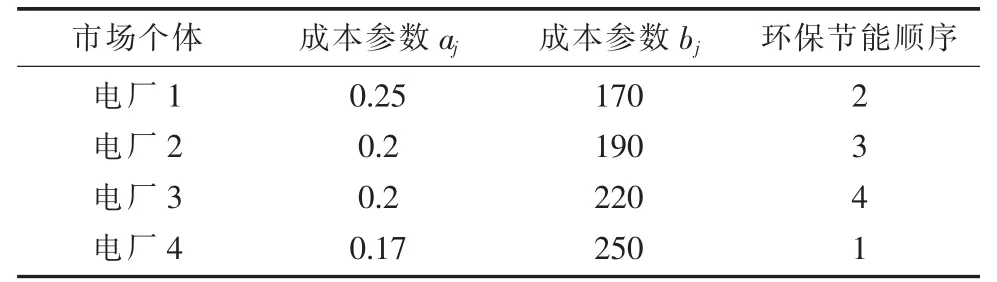
表2 电厂参数设置情况

3.2 仿真分析

3.2.1 统一出清结果

由图2 可以看出，市场中各主体收益经过一定代数后趋于稳定，其中，用户1 和电厂1 具有较高的收益，稳定情况下市场出清价格为282元/MWh。种群进化初期，市场各主体收益波动剧烈，主要是因为各主体成本函数和效益函数不同，报量和报价均处于试探过程。市场竞价在300～500代过程处于稳定，后又剧烈波动，主要是由于市场中部分个体重新改变自身报价策略。进一步的博弈过程中，用户1 的收益增加，市场各主体的报价策略也随之改变，主要是因为用户1 与电厂1 为竞价过程中的边际用户和边际电厂，当非边际主体报价接近出清价格时，边际主体通过降低自身报价提高成交电量进而促进收益的提高。

图2 统一出清下用户和电厂收益情况

由图3 可以看出：市场稳定情况下，电厂1申报电量剧烈波动，申报电价维持不变；电厂2、电厂3、电厂4 申报电量均维持不变，但申报电价均大幅波动。可知，电厂1 为出清过程中的边际电厂，因此收敛情况下，边际成交价格即为电厂1的申报电价282 元/MWh，非边际电厂的申报电价对市场出清过程并无影响。稳定情况下，电厂2、电厂3、电厂4 的申报电量分别为460 MWh，310 MWh，188 MWh。

由图4 可知：市场稳定情况下，用户1 的申报电价维持在282 元/MWh，其为边际用户；用户2、用户3、用户4 为非边际用户，其申报价格处于波动情况，且都大于用户1 的边际申报价格，对市场出清并无影响。稳定情况下，用户1、用户2、用户3、用户4 的申报电量分别454 MWh，371 MWh，347 MWh，196 MWh，满足边际价格下的最优申报电量。分析可知，市场中用户侧均达到边际价格对应的最优成交电量，此时市场处于供大于求的阶段。边际电厂1 按照自身成本申报电量电价，其满足边际用户1 对应边际出清价格下的电量需求，但自身未达到边际价格下最大成交电量，由此造成边际电厂的申报电量存在随机性，但都大于410 MWh。同理可知，当市场处于供小于求的情况，边际用户的申报电量将处于波动情况。

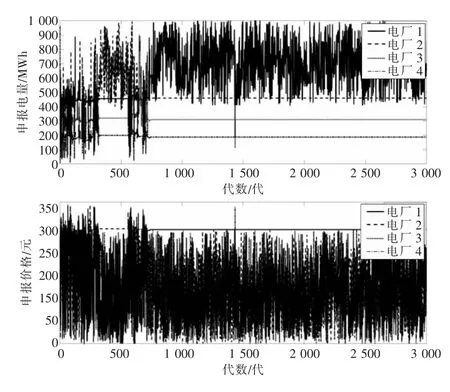
图3 统一出清下电厂申报情况

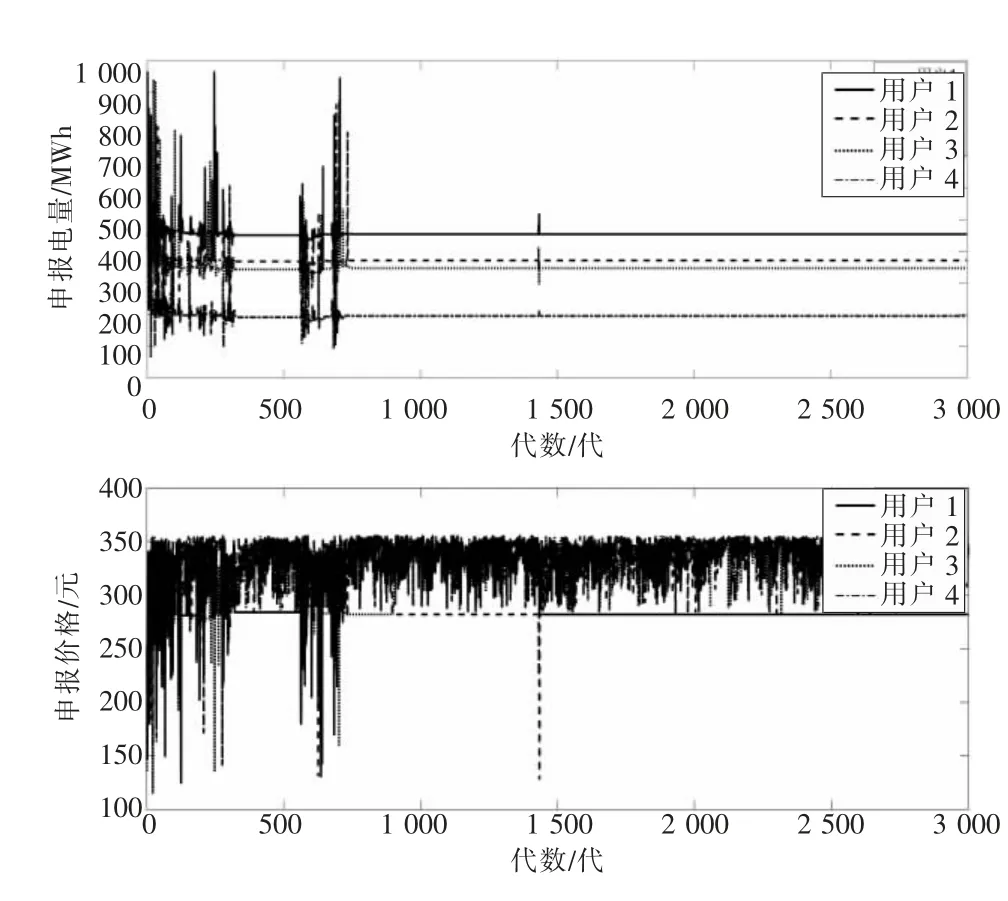
图4 统一出清下用户申报情况

3.2.2 撮合出清结果

由图5 可以看出，购售电双方在市场初期就达到了仿真均衡，其中，电厂1 和用户1 具有较高的收益，稳定情况下，电厂1 的收益为24 642元，用户1 的收益为72 686 元。

图5 报价撮合出清下用户和电厂收益情况

由图6 可以看出，撮合出清机制下，除电厂3 外的其他电厂申报电量很快达到均衡状态，且在该机制下电厂侧报价趋于一致，为281 元/MWh。主要是由于按照高低匹配出清机制，申报价差对越高成交的概率越高，市场出清价为购售双方申报的均价，市场主体为了避免无法撮合，其报价意向将趋于统一价格。但实际撮合过程中，在申报相同价差对的情况下，按照电厂环保节能顺序优先级别，电厂3 处于最劣势，因此其成为边际电厂。

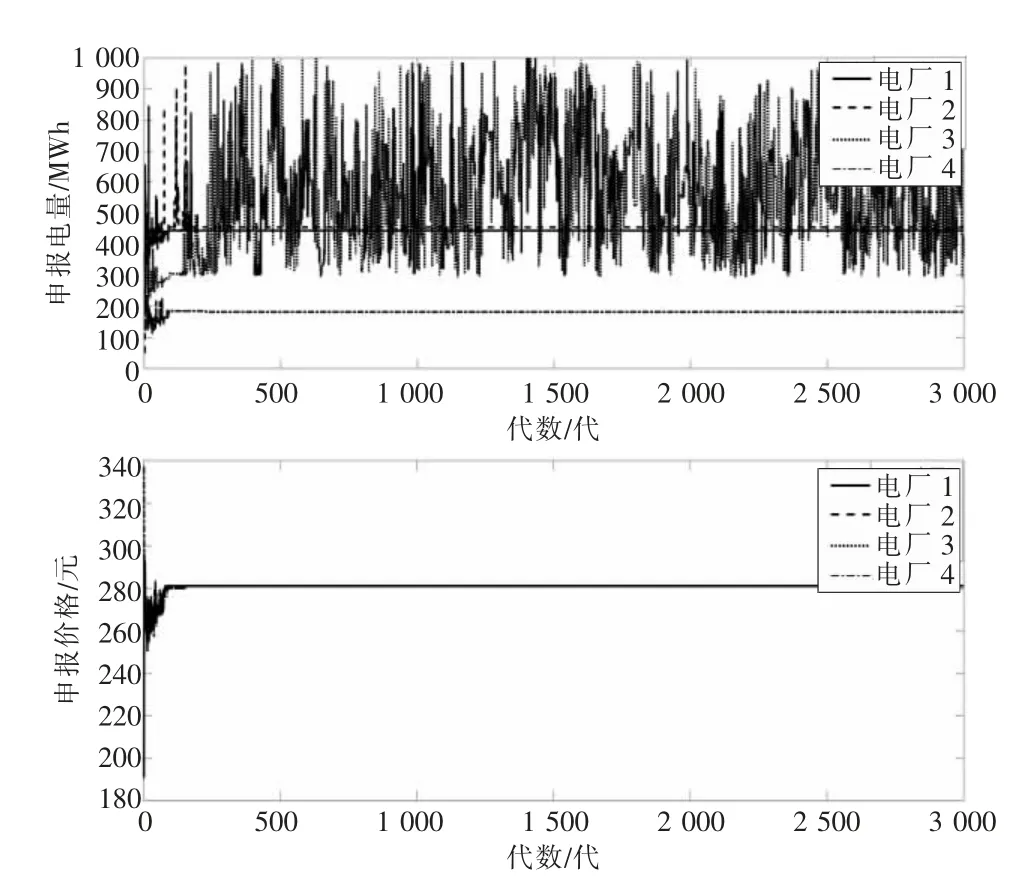
图6 撮合出清下电厂申报情况

图7 可以看出，市场用户的申报电量很快就达到均衡状态，撮合出清机制下用户的申报电价也趋于统一，为281 元/MWh。此时，用户侧对应边际价格下的最优申报电量均得到满足，分析可知，此时市场处于供大于求的阶段，依据规则，3号电厂为环保节能顺序最差的电厂，因此处在最后一位出清，其成本较低，因此有较大意愿申报富足电量，市场申报购电电量全部撮合，此时，3号电厂申报电量存在随机性，但都大于293 MWh。

3.2.3 实验结果讨论

由表3 和表4 可以看到，统一出清下电厂和用户实际申报信息的范围大于撮合出清，其波动性较高。统一出清下除电厂1 外，其他成员均满足边际价格下最优成交电量。统一出清下边际价格为282 元/MWh，撮合出清下边际价格为281元/MWh。由以上两种实验方案可得到如下结论：

（1）统一出清机制较报价撮合出清机制波动更为剧烈，其收敛至稳定解的代数更久，主要原因在于统一出清下市场边际用户和边际电厂决定了市场的边际价格，其他成员申报价格对市场出清点无影响，申报价格随机性较高，仅追求边际价格下最优的成交电量，因此模拟过程中前者收敛时间较长。两种出清机制下稳定的市场边际价格基本一致，用户侧和电厂侧收益情况差别不大。

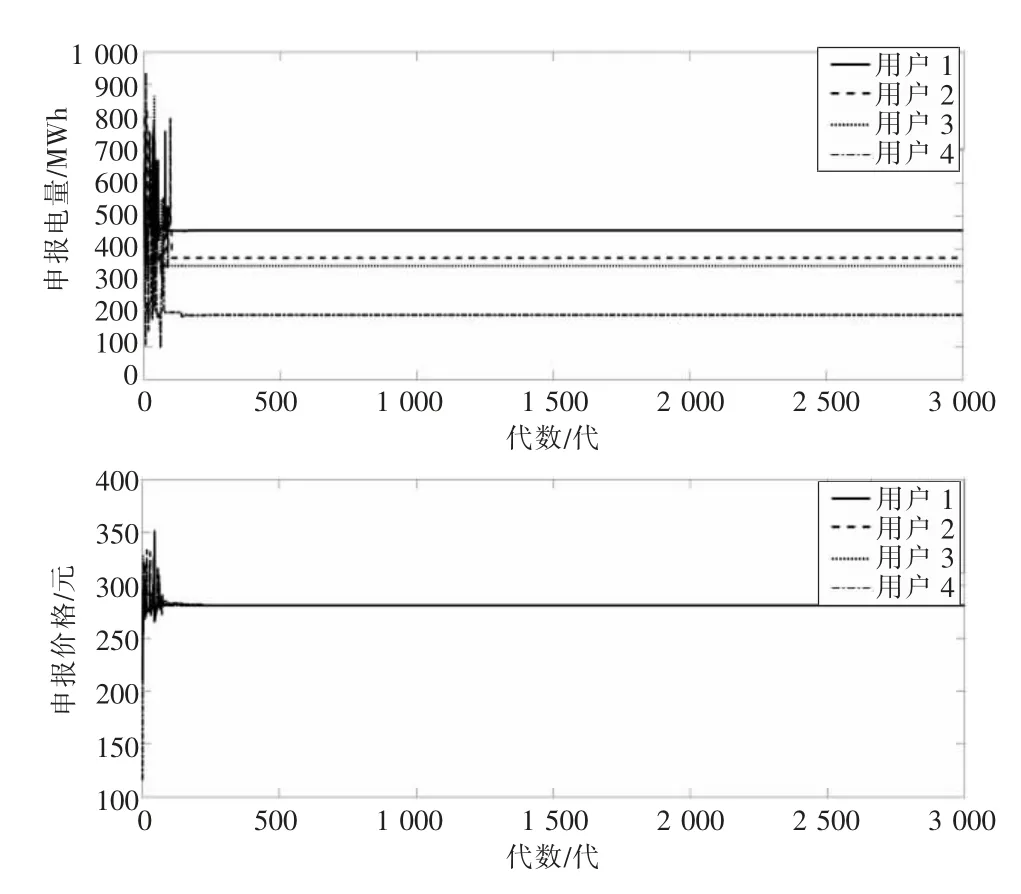
图7 撮合出清下用户申报情况

（2）统一出清机制下，市场出清价格取决于边际机组，因此稳定情况下边际电厂和边际用户的申报电价将维持不变，非边际个体申报电价将持续波动。报价撮合出清机制下，市场主体为避免无法形成有效匹配对导致竞价失败，将会产生一定的趋同效应，即收敛情况下市场上各主体的申报电价将趋于一致，且维持不变。

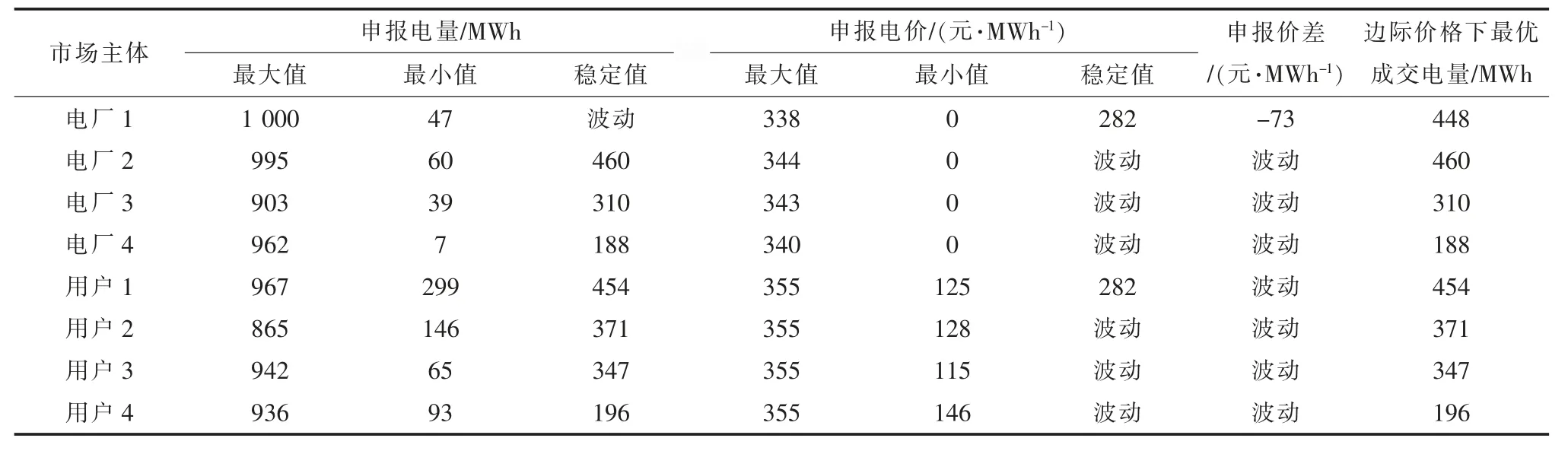
表3 统一出清下市场成员申报情况

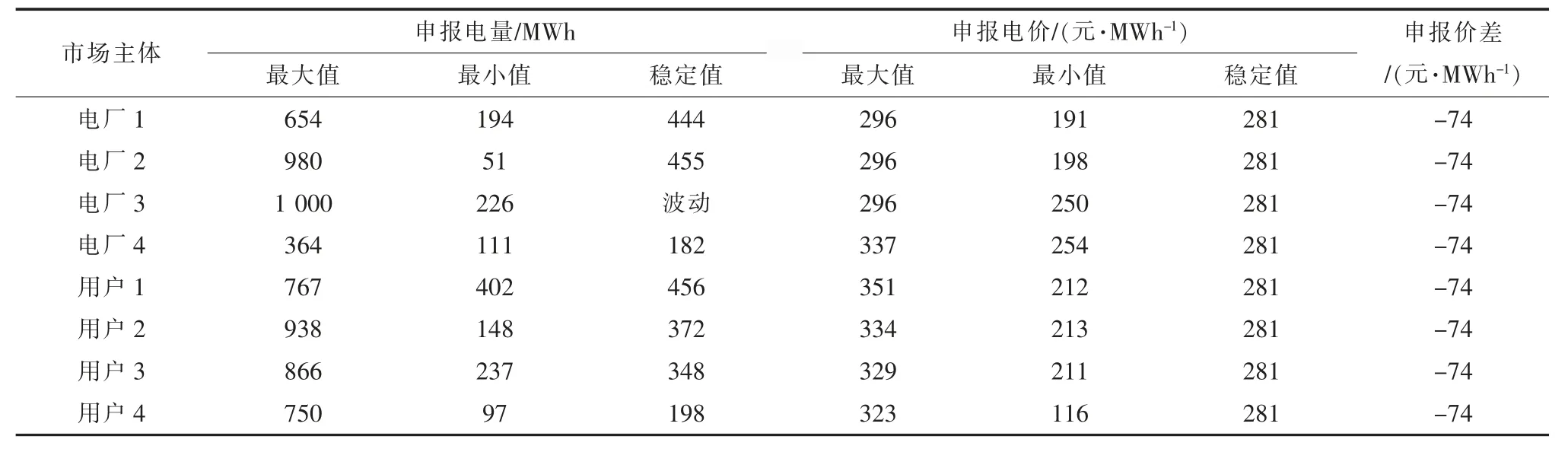
表4 撮合出清下市场成员申报情况

（3）用户和电厂以自身利润最大化为目标进行市场博弈，有可能出现供大于求或供不应求的情况，供需情况取决于边际机组和用户追求自身效益最大化情况下的最优成交电量。依据统一出清机制，供大于求情况下，边际电厂的申报电量将持续波动；供不应求情况下，边际用户的申报电量将持续波动。依据报价撮合出清规则，用户侧的申报电量符合其申报价格对应的最优成交电量，环保节能顺序最差的电厂其申报电量存在随机性，其他电厂按照其成本报价。供小于求的情况下，电厂侧申报电量均按照成本申报，用户侧平均分摊电量，但都无法达到最优申报电量。