覆冰导线动态风偏简化计算方法及影响因素分析

卞 荣，徐 雄，王一枫，楼文娟

（1.国网浙江省电力有限公司经济技术研究院，杭州 310008；2.国网浙江省电力有限公司绍兴供电公司，浙江 绍兴 312000；3.浙江大学 建筑工程学院结构工程研究所，杭州 310058）

0 引言

我国是世界上输电线路遭受冰冻灾害最严重的地区之一。 对于输电线路因覆冰引起的灾害事故，线路过载、脱冰跳跃、覆冰舞动已有大量学者进行了研究，但覆冰导线的风偏问题却鲜有研究涉及。导线覆冰之后，一方面所受重力会增加，另一方面迎风面积和所受风荷载也会相应增大，难以直接判断出覆冰对绝缘子串风偏角的影响。

大气层中的过冷却水滴在下降过程中接触到地面附近温度较低的物体（如铁塔、导线）时，会冻结形成覆冰。 文献[1-2]指出，根据形成的气象条件和物理性质，覆冰可以分为雨凇、混合淞、雾凇和积雪等多种形式，其中雨凇和混合淞由于密度较大（0.5～0.9 g/cm3）、粘附力强，对输电导线最为不利；而雾凇、积雪的密度小（0.1～0.5 g/cm3）、粘附力弱，在大风作用下容易消散。 对于导线的覆冰形状，曾黎玉[3]指出导线覆冰往往在迎风面上先出现扇形或新月形覆冰，而档距长、直径细的导线在不均匀覆冰的扭矩作用下最终易形成圆形或椭圆形覆冰。 肖正直[4]等通过输电导线的结冰风洞试验，研究了导线覆冰量及覆冰形状与风速的关系，随着风速条件的不同，导线的覆冰可能呈新月形（准椭圆形）以及扇形（或D 形）等典型形状。 此外，不同覆冰形状的导线气动力参数各异且与裸导线截然不同[5]。

可以看出，对于覆冰导线的风偏响应问题，除了线路本身结构参数和风场特性，还需考虑导线的覆冰形状、密度、厚度和气动力参数，计算工况非常复杂，需要一种准确、快速的计算方法。 目前国内电力行业标准采用单摆模型[6]来计算绝缘子串风偏角，该方法形式简洁、物理含义明确，但并未考虑风荷载的脉动效应，也没有考虑导线覆冰的情形。 文献[7]也指出，当线路存在较大的导线支座高差时，单摆模型的计算结果误差较大，需要进行高差修正。 基于脉动风速模拟和有限元计算的时域分析方法[8]可以获得较为准确的风偏角结果，但不便于大量的参数化分析和工程设计计算。 在此基础上，楼文娟[9]等提出输电线路风偏响应的频域计算方法，该方法在获得准确计算结果的同时拥有更高的计算效率，但仍需要模型建立等较为繁琐的准备工作。

本文以导线在自重和平均风荷载作用下的静力平衡构型和几何刚度作为初始条件，推导出导线的等效静力风荷载；以单摆模型为基础并考虑导线覆冰的情形，引入等效静力风荷载和高差修正系数，提出覆冰条件下输电线路动态风偏角的简化计算方法，并结合某真实线路采用时域法检验了该简化算法的准确性；以圆形覆冰导线为例，考虑不同的覆冰厚度、密度和风速，采用动态风偏角的简化计算方法对该真实线路的覆冰风偏响应进行参数化分析，得出风偏角随冰厚、密度和风速的变化规律，为输电线路的设计提供了参考。

1 多跨导线的等效静力风荷载

导线虽是一种具有显著几何非线性特征的结构，但通常情况下导线高度处的大气湍流度较小，导线风偏响应的脉动部分可视为在自重与平均风荷载共同作用下的平衡状态位置（平均风偏状态）附近的小位移振动[10]。 其计算模型如图1 所示，其运动方程可表示为：

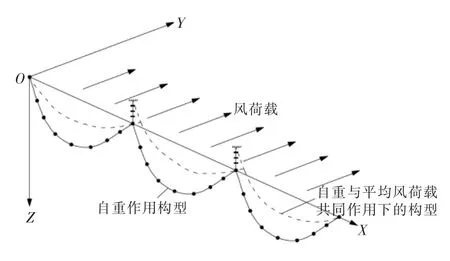
图1 导线计算模型

结构的脉动响应分为背景响应和共振响应两部分，其中背景响应可以看做脉动风荷载的准静力效应，而共振响应则是脉动风荷载中与结构自振频率接近的部分引起的动力放大作用。 文献[11]通过有限元计算指出，在我国规范规定的设计风速下，导线风致响应的共振分量因气动阻尼效应而大幅降低，计算中可忽略不计。 美国ASCE 规范[12]同样认为可以不考虑导线风致响应的共振分量。 可见，用导线风偏的背景响应均方根代替脉动总响应均方根并不会造成太大的误差，可以满足工程要求。 因此，将导线的等效静力风荷载表示为平均响应等效静力风荷载和背景响应等效静力风荷载的线性组合，其中与平均响应对应的等效静力风荷载即为导线所受的平均风荷载，与背景响应对应的等效静力风荷载可由准静力计算方法求得[13]。

我国输电线路设计规范采用风荷载调整系数βc来考虑风荷载的动力放大效应，这与等效静力风荷载的思想相同。 将风荷载调整系数βc定义为等效静力风荷载与平均风荷载的比值，即：

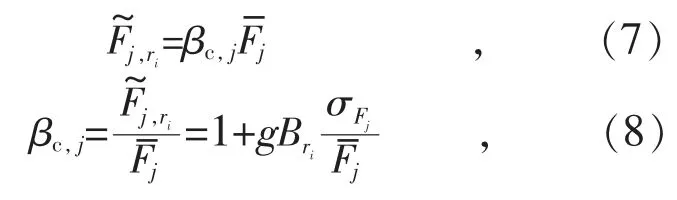
基于准定常假设，式（8）可以简化为：

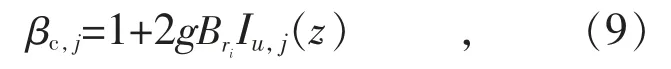
式中：Iu，j（z）为j 位置处顺风向湍流度。

对输电线路而言，顺风向湍流度在导线高度变化范围内取值差别不大，若以目标区段内导线有效高度处的湍流度Iu为基准计算风荷载调整系数，则有：

可以看出，采用式（10）计算时，整个目标区段内的所有导线节点均采用同一个风荷载调整系数，更方便在实际工程中应用。

对同一个等效目标，采用GLE 法计算的荷载折减系数Bri在导线不同位置是相同的。 但采用式（4）—（6）来计算该荷载折减系数需要知道脉动风荷载的标准差、协方差和导线平均风偏状态下的影响系数等参数，仍需要进行繁琐的计算。 为此，参考美国ASCE 规范[12]对导线阵风响应系数Gc的定义：

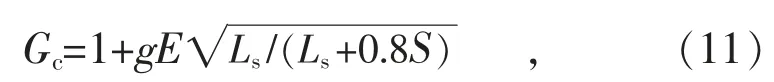
式中：E 为与湍流强度相关的系数；S 为档距；Ls为湍流积分尺度。

阵风响应系数Gc从结构响应出发，综合档距、地形、湍流积分尺度的影响，用于考虑风场脉动风速对结构静力风响应的动力放大，与风荷载调整系数βc含义非常接近。 结合式（10）和式（11），可采用式（12）来计算荷载折减系数Bri：

其中E 可参考该规范取值，其他参数也易获得，因此采用该式计算更为简便。

2 动态风偏简化计算方法

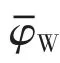
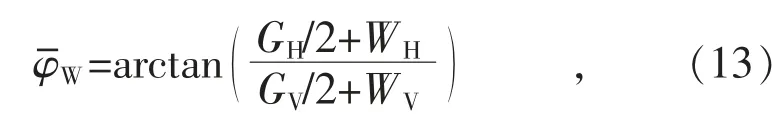
其中WH和WV可以表示为：

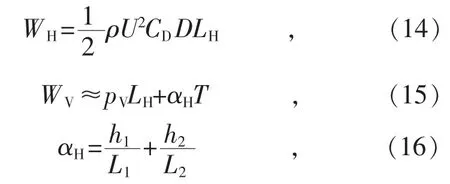
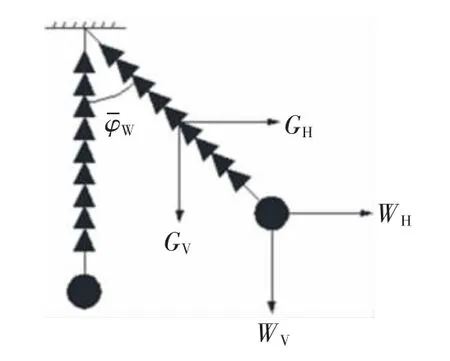
图2 单摆模型

式中：ρ 为空气密度；CD为导线的阻力系数；D为导线直径；U 为跨度内的有效高度处平均风速；pV为导线单位长度内的重力荷载；LH为水平档距，其值等于左右两跨导线档距L1和L2的平均值；αH为高差系数；h1和h2为该挂点与左右导线挂点的高差，比左右两侧挂点高时为正；T 为导线有风时的张力。

单摆模型具有受力明确、计算简单的特点，在工程上应用起来较为方便。 但单摆模型作为一种静力计算方法，既不能考虑导线覆冰时的工况，又没有考虑脉动风荷载的放大作用，会低估绝缘子串的风偏角。 此外，文献[7]指出，单摆模型对导线重力荷载WV的估算在挂点高差较大时误差较为明显，需要对式（15）中第二项乘高差修正系数k 进行修正。 该文针对大量不同支座高差线路，分别采用有限元法和单摆模型计算绝缘子串风偏角φFEM和φMOD，随后以高差系数αH为自变量，采用式（17）对tanφMOD/tanφFEM与αH的关系进行拟合，最后得到k=0.741 5 的结果。

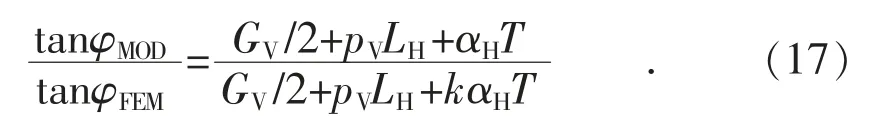
本节首先考虑导线覆冰对水平风荷载和竖向重力荷载的影响。 同时对刚性直棒法进行修正，即对于水平向的风荷载，以导线和绝缘子串覆冰状态下的等效静力风荷载Wice，eq和Gice，eq代 替 原有的平均风荷载WH和GH；对于竖向的重力荷载，以导线和绝缘子串覆冰状态下的重力荷载Wice，V和Gice，V代替原有的重力荷载WV和GV，并引入高差修正系数k 来减少因可能存在挂点之间的大高差而引起的误差。

由等效静力风荷载的定义可知，经荷载修正后计算得到的风偏角与动态风荷载作用下的峰值风偏角等效，可以视为动态风偏角。 以圆形均匀覆冰为例，对覆冰密度为ρice、覆冰厚度为d 的导线，其动态风偏角可按式（18）计算：

其中覆冰导线的等效静力风荷载Wice，eq和修正后的重力荷载Wice，V分别为：

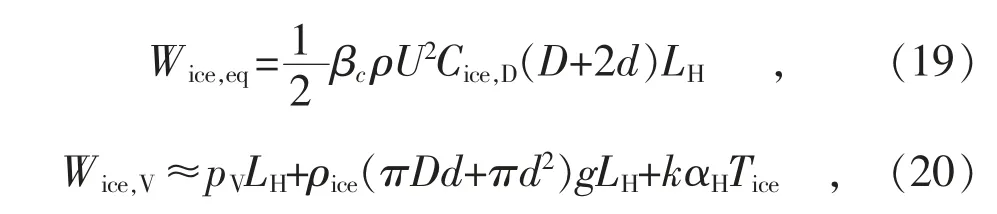
式中：Cice，D为覆冰导线的气动力系数；Tice为覆冰导线有风时的张力。

可以看出，式（19）中考虑了风荷载调整系数及覆冰厚度对迎风面积的影响；而式（20）中第二项为覆冰后增加的重力荷载，第三项考虑了高差修正和覆冰对有风时张力的影响。 对于绝缘子串覆冰后的等效静力风荷载Gice，eq和重力荷载Gice，V，其计算方法与导线类似，且无需考虑高差修正，因此不再赘述。

3 对动态风偏简化计算方法的验证

对于输电线路风偏问题，日本和部分北美学者在早期开展过实测和风洞试验研究[15-16]。 但随着计算机技术的发展，目前国内外学者多采用非线性有限元计算来获取输电线路的风偏响应，并指出了该方法具有足够的精度[8-9，17-18]。 因此，本文采用非线性有限元方法来验证该简化算法的准确性。

3.1 计算模型和参数

以某1 000 kV 特高压交流输电线路的N6 直线塔为中心，按照线路的实际档距、挂点高差等参数，建立了四跨输电线路的精细化模型，线路的几何参数和挂点编号如图3 所示。 为提高计算效率，将八分裂导线等效为单导线，绝缘子串和导线的型号及物理参数如表1 和表2 所示，其中绝缘子串和八分裂导线的阻力系数均由节段模型的风洞试验得到[19]。 线路所处地区为B 类地貌，10 m 高处基本风速按我国输电线路设计规范[20]取为27 m/s。

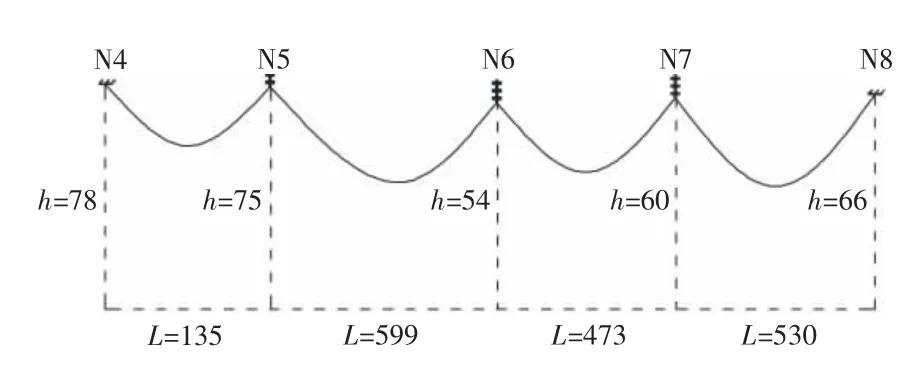
图3 某1 000 kV 特高压线路模型

表1 54×XWP-300 绝缘子串物理参数

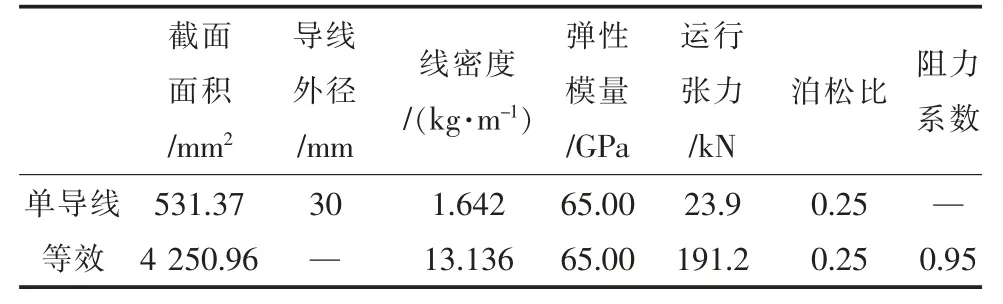
表2 LGJ-500/35 单导线物理参数及等效参数

采用有限元分析软件ANSYS 建模，输电导线采用LINK10 单元，每10 m 划分一个单元；绝缘子串采用LINK8 单元，考虑到特高压输电线路绝缘子串较长，在大风下可能发生局部转动，每个绝缘子串划分为9 个单元。 由于导线跨中弧垂与跨度之比小于1/8，导线在自重作用下的初始构型可近似采用抛物线方程确定。

分别采用动态风偏的简化计算方法和有限元时程分析求解出N6 塔处的绝缘子串动态风偏角，并将两者的结果进行对比。

3.2 动态风偏简化方法计算结果

分别采用式（9）中离散化和式（10）中平均化风荷载调整系数2 种表达形式，运用简化计算方法求解N6 塔的动态风偏角，离散化计算结果记为结果1。 式（10）中的平均风荷载调整系数为βc，以N6 塔的水平档距LH内导线为对象，分别采用式（4）—（6）和式（12）求解荷载折减系数Bri。 2 种方法求得该区段内的平均风荷载调整系数βc分别为1.292 和1.313，风偏角结果分别记为结果2和结果3。 峰值因子g 取2.5，三者的计算结果如表3 所示。

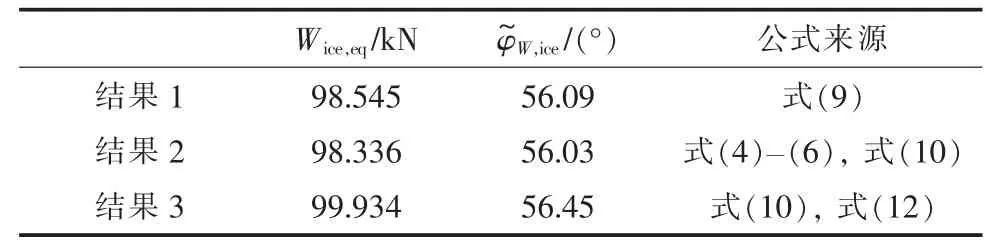
表3 动态风偏角计算结果

由计算结果可知，2 种平均化计算虽然做了一些近似处理，但其结果与离散化计算非常接近，可以认为是准确的。 采用式（10）和式（12）的平均化计算方法公式简洁、计算量最小，更适合在工程上应用。

3.3 有限元时程分析

采用谐波叠加法并考虑空间相关性，生成该四跨线路各节点的脉动风速时程。 根据准定常假设，可以将风速时程转换为风荷载并在ANSYS中施加给各节点。 计算时考虑气动阻尼的影响并激活大变形和应力刚化选项，根据N6 塔导线挂点处的顺风向位移时程结果可以换算得到该塔处的绝缘子串风偏角时程。 时程分析总长度T=2 048 s，每步时间间隔Δt=0.062 5 s。 图4 为N6 塔导线挂点处的风速时程，图5 为该塔的绝缘子串风偏角时程结果，表4 为该塔绝缘子串风偏角的统计结果。 表4 中φW，ice为计入了脉动风荷载影响的绝缘子串风偏角峰值，可以表示为：

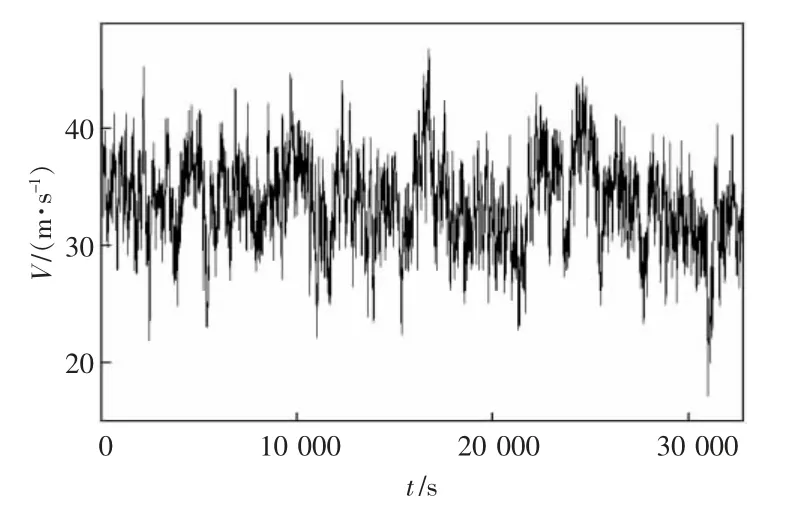
图4 N6 塔导线挂点处风速时程

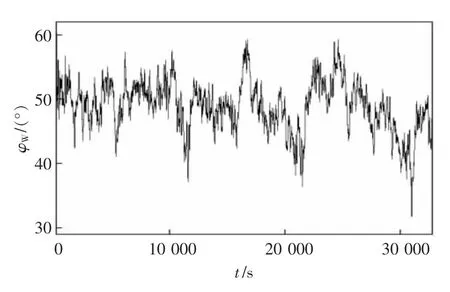
图5 N6 塔导线挂点处风偏角时程

表4 N6 塔绝缘子串风偏角统计结果对比

对比2 种方法的计算结果可以发现，基于简化计算方法的动态风偏角比有限元时程分析的风偏角极大值略小，这是因为动态风偏的简化计算方法中等效静力风荷载只计入了背景响应的贡献，没有包含共振响应的贡献。 若视有限元时程分析结果为准确值，采用简化计算方法得到的动态风偏角的误差也仅为4.8%，完全可以满足工程需要，也更适合用于覆冰导线动态风偏的参数化分析。

4 覆冰导线动态风偏影响因素分析

导线覆冰时往往总是先在迎风面上出现扇形或新月形覆冰，然后在偏心荷载的作用下导线发生扭转，会使覆冰较少的表面转到迎风面继续覆冰。 特高压输电线路档距长且子导线线径相对较小，因此其扭转刚度小，更易形成圆形覆冰[3]。

对于理想的圆截面覆冰导线来说，覆冰会使导线的重量和迎风面积均增大，难以直接看出其对绝缘子串风偏角的影响。 本节以图3 的四跨线路为基础，考虑不同覆冰厚度d（如图6 所示）、覆冰密度ρice和10 m 高处基本风速V0，采用动态风偏的简化计算方法研究不同覆冰条件对N6 塔处绝缘子串风偏角的影响。

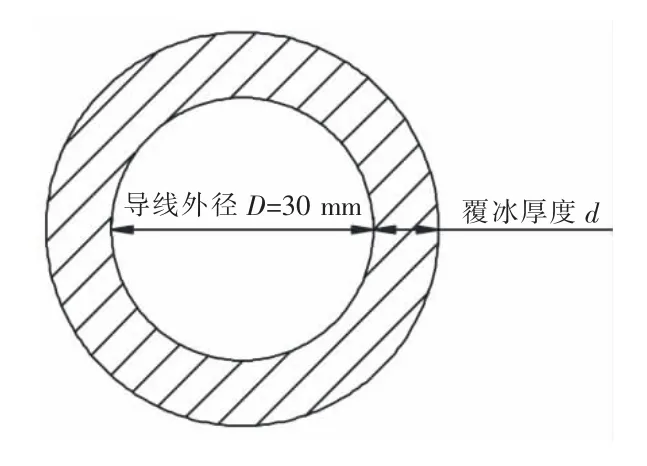
图6 理想圆截面覆冰导线

对于工况的选择，我国重覆冰架空输电线路设计技术规程[11]给出了中冰区和重冰区的覆冰气象条件：中冰区设计冰厚为15～20 mm，设计风速10 m/s；重冰区设计冰厚20～50 mm，设计风速15 m/s。 考虑到可能出现的极端恶劣冰风气象条件，本节10 m 高处基本风速V0选为10 m/s，15 m/s 和20 m/s。 过大的覆冰厚度会导致导线弧垂最低点的张力过大而不满足规范要求，结合该线路使用的LGJ-500/35 导线物理参数，覆冰厚度d可取5～30 mm。 覆冰密度根据文献[1]，选取粘附力强的混合淞的密度，即0.5～0.9 g/cm3。 为直观体现出覆冰对风偏角的影响，计算时圆形覆冰导线的整体阻力系数同裸导线，取为CD=0.95。 计算结果如图7 所示。

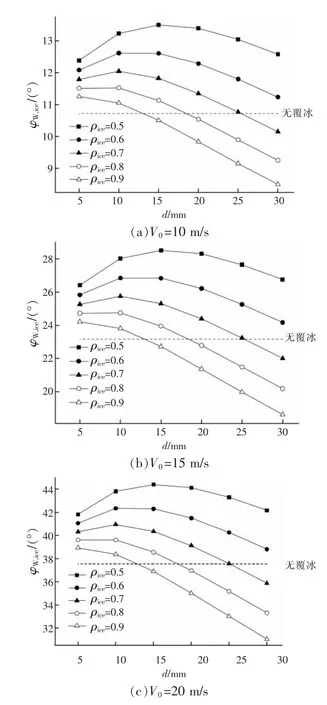
图7 圆截面覆冰导线风偏角结果

由图7 可知，3 种风速条件下圆截面覆冰导线的风偏角随覆冰密度和冰厚的变化规律基本一致。风偏角随风速的增加而增加，随覆冰密度的增加而减小。 对于较小的覆冰密度（0.5～0.7 g/cm3），风偏角随着冰厚的增加，呈现出先增大后减小的规律，在10～15 mm 区间达到最大；而对于较大覆冰密度（0.8～0.9 g/cm3），风偏角基本呈现出一种随着冰厚单调减小的规律，在5 mm 附近达到最大。由图7（c）可知，在V0=20 m/s 的情况下，圆截面覆冰的最大风偏角能达到44°以上，对于线路的正常运行已经非常不利。

将覆冰工况与无覆冰的情况（如图7 中虚线所示）进行对比可以发现，在覆冰密度较小时绝大多数工况的风偏角比无覆冰时大，即便在覆冰密度较大时，覆冰厚度较小的工况的风偏角也仍会大于无覆冰时。 因此从风偏的角度来讲，在很多情况下覆冰对于输电线路是不利的，需要在设计上引起重视。

5 结论

本文以导线平均风偏状态下的构型和刚度作为初始条件，综合考虑导线响应的平均分量和背景分量，并采用GLE 法得到了导线的等效静力风荷载。 在此基础上提出了输电线路的动态风偏简化计算方法，即以等效静力风荷载代替原静风荷载并引入高差修正系数对导线的重力荷载进行修正，随后采用时域法验证了该方法的准确性。最后基于该简化算法，对圆形均匀覆冰导线的动态风偏响应进行多工况的参数化分析，得到风偏角随覆冰密度、覆冰厚度和风速的变化规律，主要结论如下：

（1）风荷载调整系数采用平均化计算的风偏角结果与离散化计算的非常接近，其结果可以认为是准确的；参考ASCE 中对阵风响应系数的定义，采用近似方法计算荷载折减系数是可行的。

（2）通过与时域法结果的对比表明，本文提出的输电线路动态风偏简化计算方法具有足够的准确性。 该方法虽未计入共振分量的影响使结果略偏小，但完全可以满足工程应用。

（3）覆冰导线的风偏角随着基本风速的增加和覆冰密度的减小而单调变大。 覆冰密度较小时，风偏角随着冰厚的增加先增大后减小；覆冰密度较大时，风偏角随冰厚的增加单调减小。 相较于无覆冰时，多个覆冰工况的风偏角偏大，在设计时需引起重视。