云环境保护竞价隐私的最佳路径算法

王 超 张 磊* 张春玲

1(佳木斯大学信息电子技术学院 黑龙江 佳木斯 154007)2(牡丹江技师学院 黑龙江 牡丹江 157000)

0 引 言

随着云技术的发展尤其是基于位置服务以及导航的广泛应用[1]，最佳路径选择已成为人们日常出行、外出旅游的首选服务[2-3]。与最短路径不同，通常情况下，最佳路径指用户在固定区间内可在最短时间或最佳体验效果的情况下到达指定目的地的移动路径[4-5]。虽然在很多情况下最佳路径就是最短路径，但是仍存在较大概率最短路径并不能满足用户的最佳体验。因此，相对于最短路径的计算，最佳路径处理计算更为复杂，但云技术的发展为最佳路径的计算带来了便捷。在云环境下，最佳路径计算一般由不同用户提供移动路径竞价，同时经过云环境比较并给予一定补偿后获得。因此，在竞价过程中，为云环境提供最佳路径信息的用户更加关心自己提供的信息尤其是竞价信息是否安全。针对云环境处理最佳路径隐私的问题，Zhang等[6]就考虑过受限最佳路径的云环境处理，并利用同态加密技术对用户信息加密实现了对最佳路径信息的隐私保护。Xi等[7]也通过使用PIR(Private Information Retrieval)方法实现了导航最佳路径竞价数据的隐私保护。Aivodji等[8]更是提出使用多方安全计算实现多用户同时最佳路径计算并保障多用户竞价隐私的处理方法。但是，当前对于竞价的隐私保护手段一般使用加密技术，并通过竞价多方与云之间的信息交互来实现竞价比较[9-10]，虽然能够有效地保护竞价隐私，但通常会由于加密处理以及密态环境下的比较导致处理效率相对较低，且很难实现多轮竞价。针对效率和多轮竞价问题，闫小勇等[11]提出最佳路径搜索的二进制协议，该方法虽然能够提升效率却又无法有效保护竞价隐私。因此，本文基于二进制前缀族提出一种可包含用户竞价隐私的云环境下的最佳路径算法。利用二进制前缀码建立前缀族，并通过对前缀族使用哈希加密的方法建立保密环境下的比较集合，然后将该集合提交给云环境，并由云环境比较后获得最佳路径。整个计算比较过程中，一方面由于使用的是前缀族，使得云环境无法在该族群内准确地识别用户提交的最佳路径竞价，另一方面由于前缀族使用哈希加密，其他竞价用户即使获得竞价信息也无法获知用户的真实竞价。同时，本文算法在处理效率上要优于同类的多方安全计算方法，既可以支持多轮竞价，又不需要在用户和云之间重复多次计算，因此其时间效率要优于现有的多方安全计算方法。

1 最佳路径竞价和前缀族

1.1 最佳路径竞价

通常情况下，云环境下的最佳路径比较可看作是一种通过云环境实现的多方竞价的网络拍卖过程，即通过由云环境提供的物质激励对协作用户提交的最佳路径进行竞价[9]，竞价获胜者能够获得物质奖励。与网络竞拍不同的是，该过程是经过比较获得竞价最低值，即最佳路径取值。因此，这种竞价过程可表示为如图1所示的最低竞价比较过程。

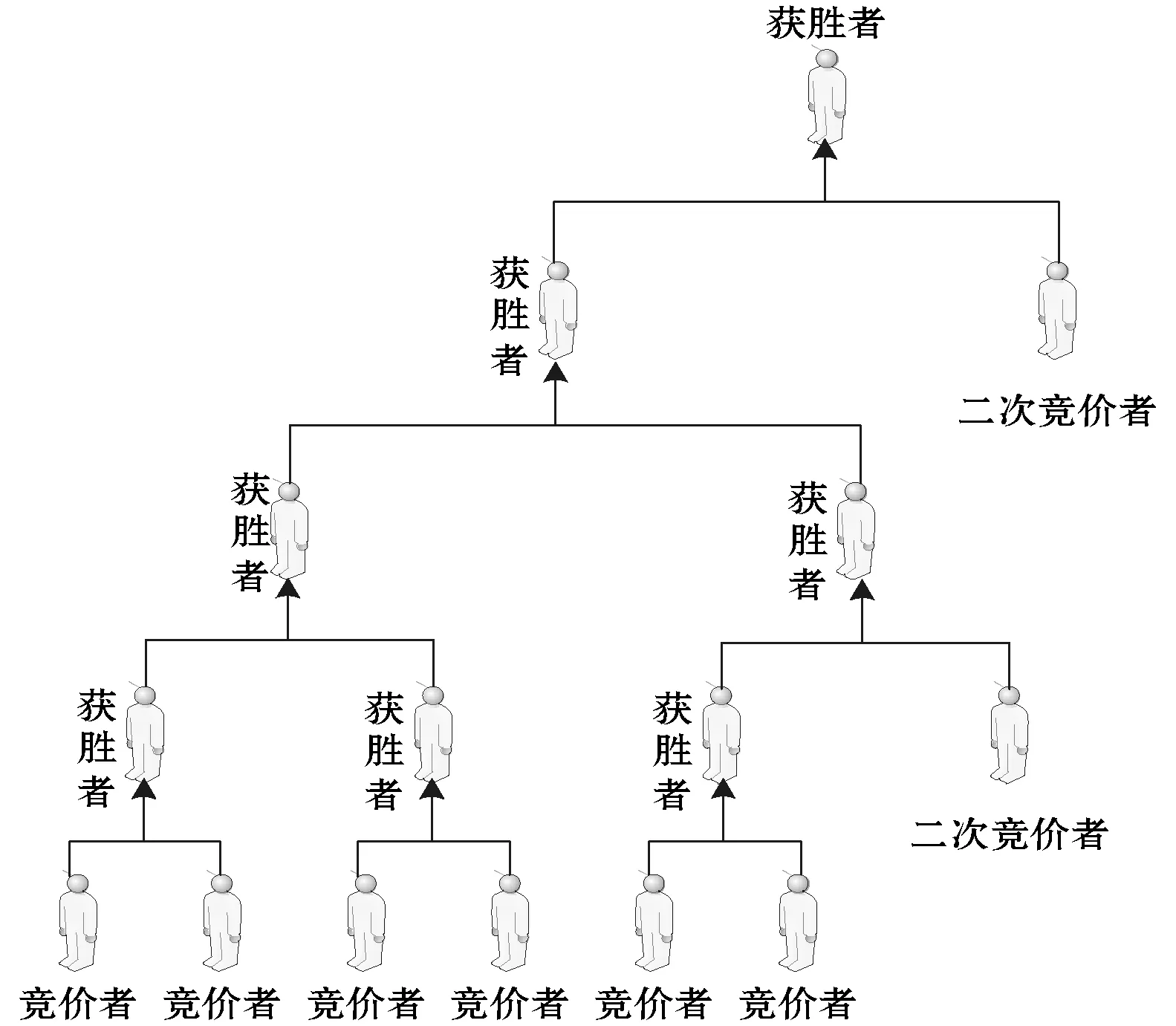
图1 云环境最佳路径的竞价过程

可以看出，在云环境下竞价者之间不仅存在一次竞价比较，还存在当前出价失败之后的二次竞价甚至三次竞价，直到不存在最佳路径竞价才能获得最后的竞价结果。因此，这种最佳路径竞价是一种多轮竞价方式，故基于加密技术实现的隐私保护单轮竞价方式无法满足需要。同时，由于在竞价的过程中，任何竞价者都不希望其竞争者获知其竞价数值，因此还需在多轮竞价中保持用户竞价隐私。

1.2 前缀族

前缀族是通过交运算来验证某一数值是否在被判定的某一区间范围内，即通过交运算来检测数值范围[12]。对于s-前缀族{0，1}s{*}w-s有s个0或者1，以及s个(w-s)*s，其中*可用0或者1来替代。例如：1***表示1-前缀族，而11*表示2-前缀族。由此，一个s-前缀族可代表一个从{0,1}s{0}w-s到{0,1}s{1}w-s之间的数值范围。例如：p=1****表示的范围是[10 000,11 111]，也就意味着一个数值满足s-前缀族当且仅当具有相同首位的s位二进制数与s-前缀族相同。假设存在w比特长度的二进制数x=b1,b2,…,bw，则关于x的前缀族可表示为F(x)={b1,b2,…,bw,b1,b2,…,bw-1*,…,b1*…*,*…*}，该前缀族有(w+1)个元素，其中第i个可表示为b1,b2,…,bw-1+i*…*。例如数字9的二进制表示是01001，则F(9)={01001,0100*,010**,01***,0****,*****}，于是有对于一个给定的数值x以及前缀p，x位于p范围内当且仅当p∈F(x)。其中，前缀族的范围[d1,d2]可表示为P([d1,d2])，该范围包含多个前缀，每个前缀覆盖范围[d1,d2]中的一个子范围，并且所有前缀覆盖整个前缀族的范围[d1,d2]。例如，p([7,25])={001111,011110,111100,111000,110000,1****}，所以，x∈[d1,d2]当且仅当F(x)∩P([d1,d2])≠∅。因此可利用前缀族这一特性制定一种隐私保护的竞拍策略，一方面防止同类竞价者获得竞价隐私信息，另一方面能够实现多轮竞价。基于这一思想，本文提出一种基于前缀族的隐私保护竞价的最佳路径算法，并以此实现隐私保护的多轮竞价。

2 基于前缀族的隐私保护竞价

2.1 隐私竞价处理

使用前缀族的隐私保护竞价可以简单地划分为两个阶段：第一阶段为最佳路径竞价的前缀族编码，第二阶段为最佳路径多轮竞价秘密比较。为了进一步增强算法的隐私保护能力，将最佳路径竞价使用哈希加密增强竞价的保密性。因此，竞价的处理可按照前缀族编码和多轮竞价秘密比较展开。

最佳路径竞价前缀族编码阶段：

第1步云平台发布指定起始点位置区域最佳路径任务，同时给出最佳路径的最高竞价；

第2步各竞价者在收到竞价任务后，将自己的竞价按照前缀族进行编码，并同时将自己的竞价与最高竞价合并建立竞价区间；

第3步各竞价者使用哈希函数对前缀族和竞价区间进行加密，并获得加密后的信息H(F(x))和H(P([d1,d2]))并发送给云平台。

最佳路径多轮竞价秘密比较阶段：

第1步云平台将收到的由各个竞价者发送的哈希值按照前缀族和竞价区间加以区分；

第2步平台执行算法1对前缀族和竞价区间加以比较并获得当前最佳路径取值；

第3步云平台发布当前竞价胜者，并同时接收第二轮竞价前缀族和竞价区间；

第4步重复执行第2、3步，直到无后续竞价。

算法1前缀族最佳路径竞价比较

输入：接收到的n个竞价者发送来的哈希加密后的前缀族集合Hi(F(x))和竞价区间集合Hi(P([d1,d2]))，1≤i≤n,k=n。

输出：最低竞价结果前缀族min(H(F(x)))。

1. for(i=1;i<=n;i++)

2. for(j=1;j<=n;j++)

3. if(Hj(F(x))∩Hi(P([d1,d2]))≠∅)

//判断集合交集

4.k=k-1;

//计算元素重合次数，即交集出现次数

5. end if

6. if(k<2)

7. min(H(F(x)))=Hi(F(x));

//获得最佳路径竞价

8. else

9. 算法执行失败；

10. end if

11. end

12. end

上述过程可表示为前缀族与竞价区间中每个子项之间的相交关系。例如：假设云环境提出的当前最佳路径竞价的最高值为25，存在4个竞价者向云环境提出竞价，且分别是2、3、5、6，则按照前缀族编码将得到表1所示的竞价前缀族和竞价区间。

表1 前缀族的竞价编码

可以看出，[2,25]这样的竞价区间与包含在该区间内的所有竞价之间的交集都不为空，则该区间为包含最佳路径区间。此时与该区间同时提交的竞价为最佳路径竞价。同时，对应于使用哈希函数加密后的集合中的每个元素，由于哈希算法的抗碰撞性上述元素交集计算成立，且由于哈希加密的单向性，上述竞价不会被包括云环境在内的各个竞价实体所获知，竞价隐私得到了保护。

2.2 安全性分析

使用前缀族在云环境下比较获得最佳路径竞价的安全性取决于包括云环境在内的各个实体无法准确地获知竞价者出价。本文算法将竞价内容转换为前缀族，使得单一竞价被扩展为一组至少由6个二进制数组成的前缀族，同类竞价用户即使通过搭线等攻击手段获得该族，也只能得到k个近似二进制竞价，准确获知用户的真实竞价的比例为1/k。在竞价过程中，用户利用哈希函数对前缀族中的每一个二进制数进行加密，而由于哈希函数的单向加密和抗碰撞特性，使得包括云服务器在内的整个参与竞价的实体均无法对所获得的竞价信息加以解密，进一步保障竞价信息的隐秘性。整个竞价的比较过程是通过利用H(F(x))和H(P([d1,d2]))进行交运算结果是否为空的比较获得最佳竞价的，整个过程中不需要进行任何的实际价值对比，同时也不似同态加密那样进行密态环境下的数值计算。因此无论云环境是否具有极强的计算能力以及信息分析能力，均无法猜测获得竞价信息，进一步保障整个竞价处理过程中的信息隐蔽性，提高了最佳路径竞价比较的安全性。

3 实验验证

为验证本文算法在执行过程中的计算效率以及算法在多轮隐私竞价方面的隐私保护能力，本文在Windows 10环境下，使用Core i7处理器，8 GB内存的笔记本电脑利用MATLAB 2017a进行模拟验证。参与比较的算法有基于编码和加密的RADP算法[12]、使用同态加密进行比价的PPSP算法[6]、基于差分隐私的TATP算法[10]以及基于加密的CMQN算法[9]。实验将在算法执行时间、最高同价竞价比较次数、竞价信息不确定性以及加密竞价的可猜测概率等方面展开比较。

图2给出了不同算法在随竞价人数增加的情况下算法的执行时间差异。可以看出，所有算法的执行时间均随着竞价人数的增加而增加，这是由于各算法需要对每个竞价进行比较。本文算法的执行时间最短，这是由于本文算法仅需进行集合交集运算，而不需要数值比较。TATP算法采用添加噪声的方法，需要同时对噪声数据进行数值比较，执行时间稍高。CMQN算法对加密数值进行比较，其比较过程需要解密后才能完成，因而其执行时间高于CMQN算法。RADP算法虽然也使用集合，但是其编码效率要低于本文算法，而且需要进行密文比较而不是集合交集运算，因此其执行时间同样高于本文算法。PPSP算法采用基于同态加密的多方安全计算方式，需要在竞价用户与云服务器之间多次进行秘密计算，算法执行时间最高。

图2 算法执行时间

图3给出了出现相同最高竞价情况下，不同算法对相同最高竞价的处理轮次。对于相同最高竞价，一般的处理方法是需要竞价用户重新进行出价，并再次进行竞价比较。从图3中可以看出，本文算法的比较次数最低，这是由于在相同竞价产生之后本文算法仅需对再次竞价用户进行竞价比较，不需要与其他已完成竞价的用户比较。RADP算法与本文算法相类似，但是需要在最后的比较中与前次比较的次优用户进行比较，因此比较次数要高于本文算法。CMQN算法采用加密实现隐私竞价，但其主要针对的是单次竞价，在重新竞价时需要与所有用户进行比较。TATP算法与CMQN算法类似，但是由于添加的噪声同样需要加以比较，因此其比较次数高于CMQN算法。PPSP算法采用基于同态加密的多方安全计算，其比较不仅需要对所有竞价重新进行秘密比较，还需要进行每个用户间的隐私竞价比较，因此最高同价竞价比较次数最多。

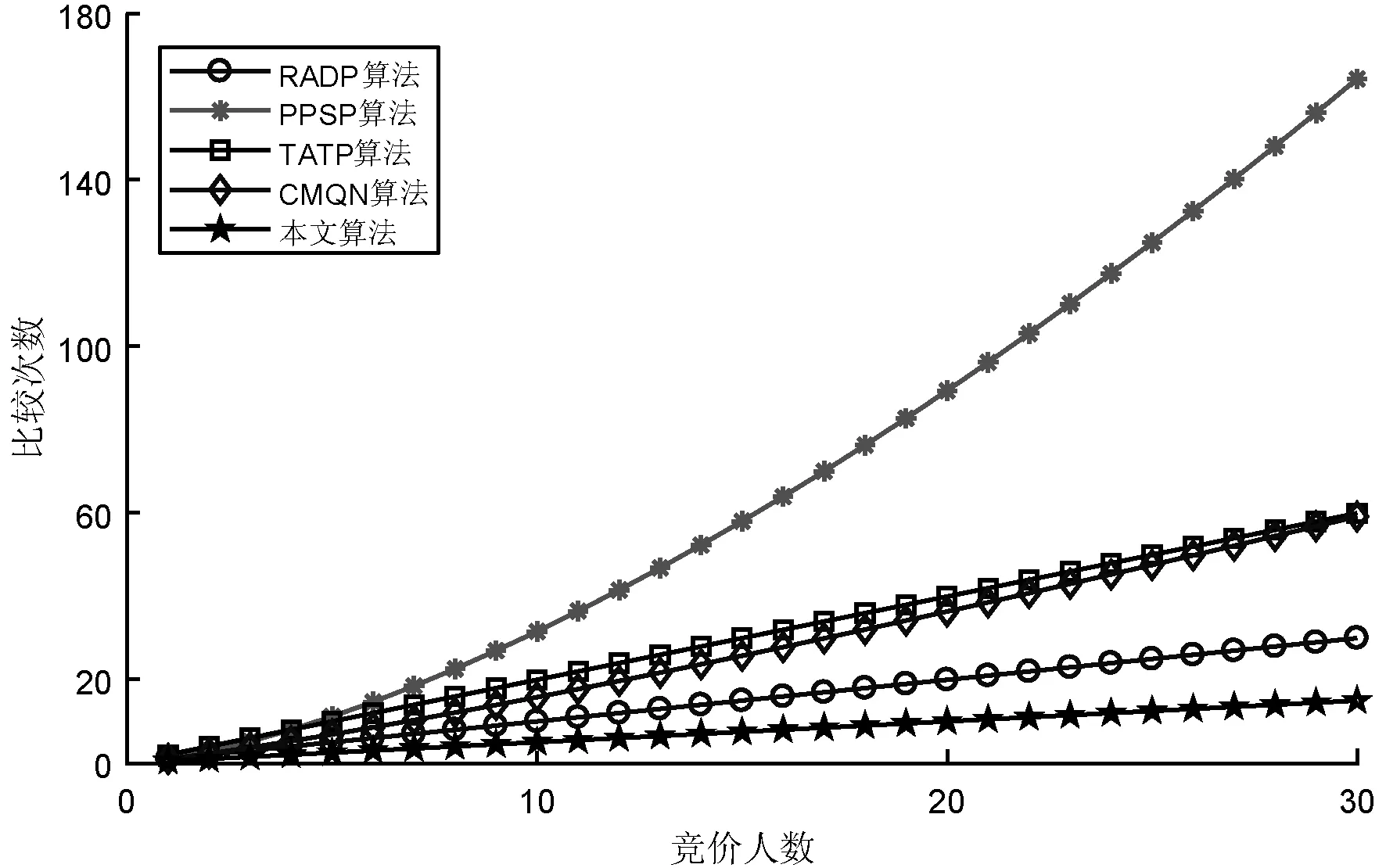
图3 最高同价竞价比较

图4给出了竞价用户提交竞价所组成的竞价集合中真实竞价的不确定性。可以看出，随着竞价人数的增加，本文算法、RADP算法和TATP算法的不确定性都随之增加，而PPSP算法和CMQN算法却未产生变化。这主要是因为CMQN算法使用加密处理，其信息不确定性并不受竞价人数影响，且始终保持竞价的单一加密性。PPSP算法尽管也是采用加密手段，但是由于同态加密的同态特性，其秘密计算是在竞价用户之间进行，所以其信息不确定性要高于CMQN算法。TATP算法通过噪声实现隐私比较，其竞价信息不确定性随用户增加而增大。RADP算法采用竞价分组模式，其竞价分组数量随竞价人数增加而增加，因而具有更高的不确定性。本文算法不仅采用竞价分组模式，而且分组数量随着竞价值位数的变化而增加，因而具有最高的不确定性。

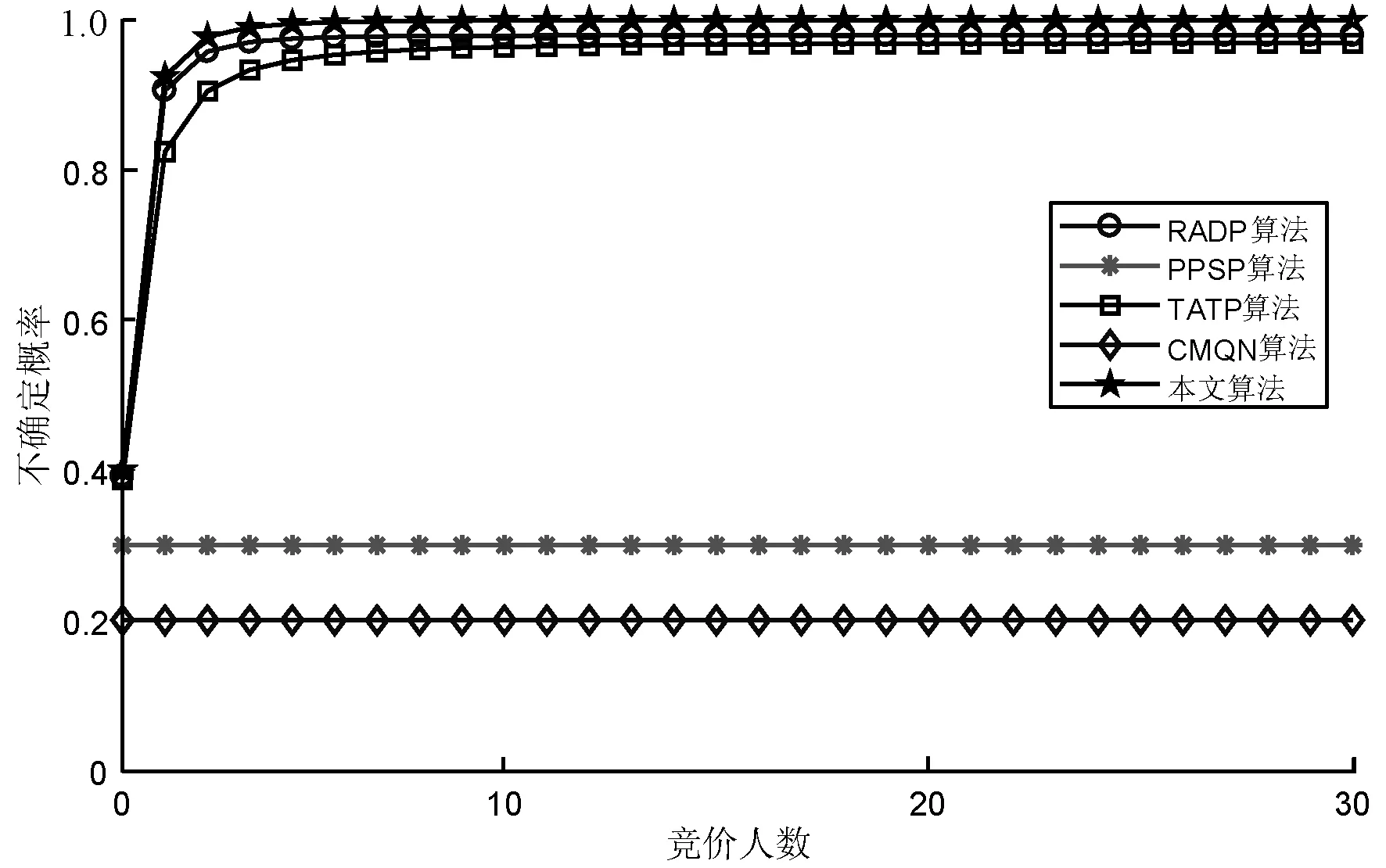
图4 竞价信息不确定性

图5给出了云环境在强计算能力下，对加密的用户竞价成功猜测的成功概率。可以看出，随着竞价人数的增加，云环境对竞价成功用户的猜测成功率逐渐降低。但是，TATP算法由于只是简单地添加了噪声竞价，因而其猜测成功率要高于其他算法。CMQN算法仅对竞价进行单一加密，这使得其猜测成功率虽然低于TATP算法但仍然很高。PPSP算法采用多方安全计算，在共谋的情况下其竞价隐私存在一定的被识别概率，因而其猜测成功率要高于RADP算法和本文算法。RADP算法采用分组后加密比较的方式实现隐私竞价比较，但是其分组数量有限，影响了该算法的隐私保护能力，因而其加密竞价的可猜测概率高于本文算法。本文算法一方面使用哈希加密后的集合交集运算，增加了竞价信息的隐私比较特性，另一方面随着竞价值位数的变化增加当前竞价分组数，进一步增加了竞价信息的不确定性，可猜测概率最低。

图5 加密竞价可猜测概率

4 结 语

为了保障在云环境处理下对用户最佳路径的隐私竞价给予保护，本文提出一种基于二进制前缀族的云环境下保护竞价隐私的最佳路径算法。一方面将用户竞价转换为泛化后的前缀族二进制编码，令攻击者无法准确识别；另一方面，将这种前缀族利用哈希函数加密为单向不可逆的加密编码，进一步加大对竞价的保护。同时，由于采用前缀族与竞价区间加密值交运算比较的方式获得最佳路径，整个计算处理过程并没有受上述处理影响而增加计算复杂度和处理负载，因此具有较好的执行效率。通过与其他同类算法在隐私保护能力与算法执行效率两个方面的比较结果也可看出，本文算法具有更好的适用性。然而，本文算法仅可用于最佳路径的竞价计算过程，仍无法解决云环境其他计算处理的隐私问题，今后的研究工作将在云环境数据隐私保护以及数据隐私利用等方面展开。