超空泡射弹高速倾斜入水的空化流动数值模拟

2019-08-13易文俊

兵器装备工程学报 2019年7期

秦杨,易文俊,管军

(南京理工大学瞬态物理国家重点实验室，南京 210094)

航行体高速入水时，在流体力的作用下,在航行体表面一部分形成低压区,当航行体最小压力点处的压力降低到饱和蒸汽压时,液体介质会发生汽化而产生空泡[1]。空化流动的流体界面上会出现较大的密度比和流场参数梯度，这给数值求解这类问题带来了很大的困难[2]。入水过程伴随着大量复杂的流动现象如湍动、相变、可压缩等，具有非定常、强瞬时及高载荷等特性，会对航行体的运动、结构性能产生严重影响[3]。

入水角度是影响航行体入水空化流场特性的一个重要因素，过小的入水角度会造成航行体忽扑或者冒出水面，不能按照近似于空中轨迹延长线在水下运动。过大的入水角度有可能使航行体不能最快到达目的点。因此选择合适的入水角度是保证航行体优良性能的重要前提。尤其近年来随着宇宙飞船和火箭发动机等在水面回收等技术的应用以及水下武器的发展，掌握入水角度对航行体入水过程流场特性的影响规律显得更加迫切和重要。

20世纪60年代Logvinovich基于大量实验和理论研究，提出了经典的基于势流理论的空泡截面独立膨胀原理，描述了运动体入水空泡生成和演化过程，为分析空泡壁面运动贡献了重要的理论成果。Savchenko等[4]对不同形状航行体空泡形态、空化器阻力特性等开展了研究。Sun等[5]采用具有完全非线性边界条件的不可压缩速度势理论，对多种不同斜角锥体的倾斜入水进行了仿真。Yves-Marie S[6]基于Wagner theory发展了数值求解三维物体入水的理论方法，通过与实验结果对比表明该方法准确可靠。熊天红等[7]对小攻角对水下高速射弹空泡形态的影响的研究表明攻角会影响空泡的对称性，从而使得航行体失去平衡。宋武超等[8]研究了不同头型回转体入水过程中空泡形态的规律、运动特性及流体动力特性。胡青青等[9-10]对不同头型钝体的超空泡流动特性在不同速度条件下进行了实验以及数值模拟。

根据已有文献，对入水问题空泡变化及流场特性的数值仿真研究，主要以垂直入水为主，然而实际中入水问题几乎都是倾斜入水。本研究采用CFD软件Ansys fluent18.2模拟二维情况下初速度为500 m/s的射弹以30°、45°和60°三个角度的倾斜入水过程，得到了不同角度下弹体入水空泡形态发展规律、弹道特性及流体动力特性变化规律，研究结果可为工程实践提供理论参考。

1 数学模型

一般默认对于初始速度不是太快的入水情况，流体可压缩性[11]可参与不考虑。本研究将流体介质视作不可压缩，同时不计流体黏性所导致的热传递。VOF多相流模型中分别用αl，αg，αv表示液体、气体和水蒸气的体积分数，它们的关系为:

αl+αg+αv=1

(1)

混合物的连续性方程为

(2)

其中：ρm为混合物密度；ρl为水的密度;ρv为水蒸汽的密度;Vm为混合物速度矢量。

混合相的动量守恒方程为

(3)

其中：ui和uj为速度分量;μm为混合介质的动力黏度;μt=ρmCuk2/ε为湍流动力黏度。其中Cu=0.09是常数，k为湍动能，ε是湍流耗散率。

ρm=αlρl+αgρg+αvρv

(4)

μm=αlμl+αgμg+αvμv

(5)

本研究采用Schnerr and Sauer空化模型对流动中的空化问题进行求解，在这个模型里水蒸汽相体积分数的输运方程为

(6)

其中：Fvap=50和Fcond=0.001为经验常数，αnuc=5×10-4为不可凝结气体积分数;RB=1×10-6m为瑞利方程中的气核半径。对于流动中的湍流现象，本研究采用k-ωSST湍流模型对流体控制方程进行封闭求解。该模型能够更恰当的描述湍流剪切应力的传输，在预测近壁区绕流和旋流有优势。

2 数值计算

2.1 计算模型

本文的数值模拟在二维情况下进行。针对截锥形头部的弹体入水问题，开展了入水角为30°、45°、60°3种工况下的高速倾斜入水数值模拟研究。射弹模型采用圆盘空化器，头部为截锥体，后体部分为圆柱体。其中，弹体材料为普通钢，密度为ρ=5 g/cm3。超空泡射弹的头部是唯一稳定的沾湿区域，还是90%以上航行阻力的来源。根据文献[12]的实验数据结果，弹体空化器直径与后体直径的比值应大于0.26。无附体超空泡射弹的尺寸参数如图1所示。

图1 射弹尺寸参数

2.2 计算域及边界条件

计算域为圆柱体，图2为其对称面示意图。根据文献[13]的数值模拟结论，流域的径向尺寸应大于46倍弹体最大直径，选取计算域直径为2 000 mm，高度为2 500 mm。气水交界面取在坐标原点下方25 mm处，空气域高为500 mm，水域高为2 000 mm。初始状态，弹体的轴线与x轴夹角为α，坐标原点取在头部中点处。外流域边界条件均采用压力出口边界(pressure outlet)，采用用户自定义函数(udf)对边界上的压力进行定义；计算环境压力P0=101 325 Pa。

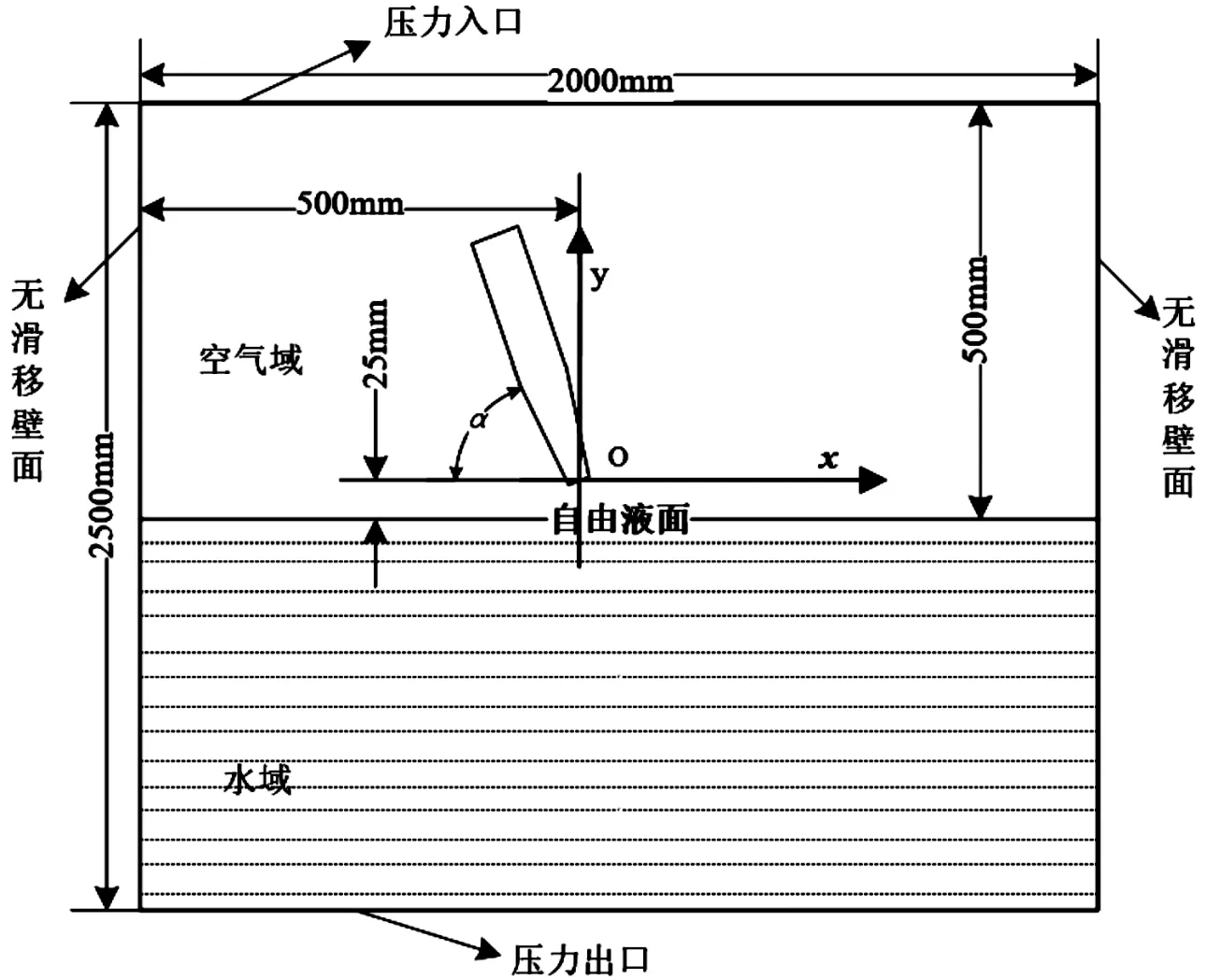
图2 计算域对称面示意图

2.3 动网格技术与网格划分

在弹体入水的数值模拟中引入动网格技术，从而实现弹体高速倾斜入水运动。由于采用三角形网格，所以选用弹性光顺模型以及局部重划模型更新网格。通过设置模型表面网格的几何尺寸，并设置尺寸变化范围，网格被压缩或被拉升超出设定网格尺寸时，就会被合并或分裂出新网格层。首先设移动边界附近的网格理想高度为hideal，网格分裂因子为αs，网格层溃灭因子为αc。当网格被拉伸，且被拉伸的网格高度hi满足式(8)[14]时，网格将根据指定的网格层高度分割网格；在网格被压缩，且网格高度满足式(9)时，被压缩层网格将与其相邻网格合并为新一层网格。

hi>(1+αs)hideal

(7)

hi<αchideal

(8)

为了在实际计算中消去网格的对流效应，引入动网格后控制体V对变量φ的守恒方程如下：

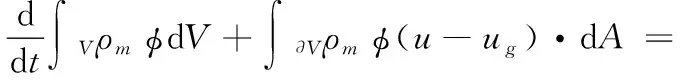
(9)

式中：ρm是流体混合物密度；u是流体速度矢量；ug为动网格的运动速度；Г为扩散系数；Sφ为标量φ的源项；∂V表示控制体积V的边界。

由于非定常问题的动网格计算常常需要计算巨量的数据，对计算机资源要求较高。因此，为了提高计算速度、改善计算精度，将计算域划分为弹体运动路径上的加密区域和受弹体运动影响较小的稀疏区域。为保证空气域、汽水交界面以及空泡区域的计算结果精度，加密区域采用较密集的网格，且对弹体周围网格进一步加密。两个区域的网格通过一组网格界面mesh interface滑移，在fluent中，通过mesh interface工具将两个区域的网格界面对接起来。网格划分结果如图3所示。

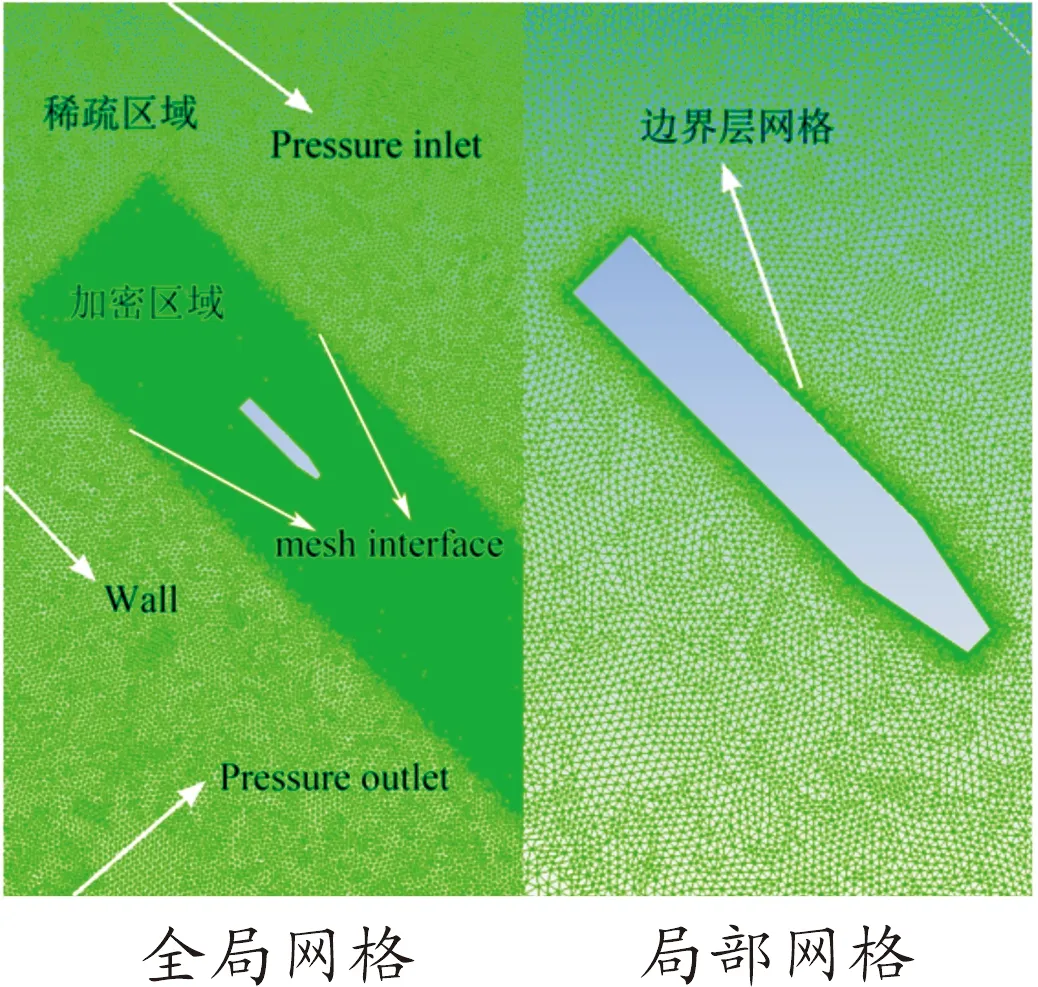
图3 流场网格

2.4 数值方法

在入水过程中，射弹的运动轨迹是由弹体自身惯性以及弹体上的作用力(重力、水动力、气动力等)和力矩共同决定的，因此弹体的运动轨迹是与流场的计算相互耦合的。本文采用Ansys Fluent18.2提供的6DOF求解器，计算倾斜入水过程中弹体表面上的作用力和力矩，然后根据力的平衡(重力、水动力、气动力等)，计算出平移加速度，再积分得到平移速度；基于力矩，计算出角加速度，再积分得到角速度，然后计算得出新的重心位置和欧拉角，最终解算出弹体倾斜入水的运动轨迹。

采用基于VOF多相流模型的有限体积法对流体控制方程进行时间和空间上的离散，在瞬态计算过程中速度与压力的耦合计算采用PISO(Pressure Implicit with Splitting of Operators)算法；时间离散为一阶精度，对流项采用Quick离散格式；压力插值采用PRESTO！离散格式；综合考虑计算时间与收敛性，采用一阶迎风格式离散动量方程。耗散项和湍流采用了二阶迎风格式；各相体积率离散采用CICSAM格式。基于C语言程序，采用UDF自编程定义入水弹体质量、惯性矩及计算域边界压力，最终实现弹体的入水运动。

3 数值计算结果验证

湍流一直是流体力学实验的难点，想要通过实验获得流场结构非常困难。随着现在计算流体力学的蓬勃发展以及计算机性能的显著提升，使用数值方法计算入水空泡流场变成了一种可行途径。

基于上文提出的数值模拟方法，采用不可压缩液体作为介质，将数值模拟结果与文献[15]的试验结果进行对比，从而检验数值模型的可靠程度。根据该文献的实验结果，获得射弹以初速为440 m/s、入水角度为10.7°的入水瞬间试验照片，根据文献中的射弹外形和运动参数，进行数值模拟，对比空泡轮廓、位移曲线和速度变化规律的数值计算结果与实验结果。

从图4可以看出，入水0.1～1.0 ms，除了喷溅形态不太一致，入水的空泡云图与试验照片具有较好的一致性。图5给出了高速射弹倾斜入水位移曲线和速度变化规律的数值计算结果，lx、vx分别表示高速射弹水平方向位移与速度，ly、vy分别表示高速射弹竖直方向位移与速度。从图5可以看出，仿真结果和文献[15]的实验数据的位移和速度变化规律吻合度也很好，这验证研究中所采用的数值模拟方法对倾斜入水过程的计算结果是正确有效的。观察图4与图5不难发现，数值计算结果能够较好地反映入水过程中空泡形态及弹体弹道特性的变化过程。

图4 空泡形态

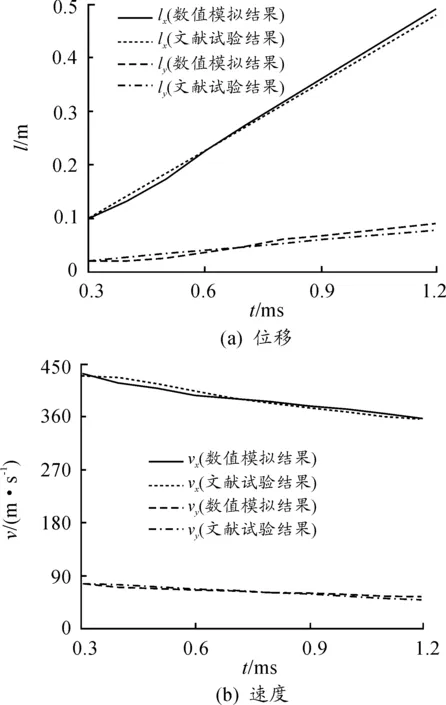
图5 位移和速度曲线

4 不同角度入水的计算结果分析

弹体浸水时的低压效应和浸水阻力不仅与头型和长径比有关，还与入水角大小有关系，本文使用数值计算的方法探讨不同角度倾斜入水过程弹体的空泡形态、弹道特性及流体动力特性变化规律。

4.1 高速倾斜入水空泡形态及流场分析

对截锥头弹体500 m/s 初始速度，入水角度分别为30°、45°、60°的倾斜入水问题开展数值模拟计算，分析不同入水角度对其空泡形态及流体动力特性等影响规律。

图6给出了弹体45°入水过程0～1 ms空泡变化过程。弹体倾斜入水时，因为头部下侧首先跟水接触，在弹体前方引起溅水，来不及逃出的空气在隆起的水堆和弹体间形成一个低压空泡区。同时，水动压力垂直于弹体的沾湿面，由于沾水面不是圆心在弹体重心的球面的一部分，因此作用于弹体沾湿面的合力将产生一个绕弹体重心的力矩，使得文中具有圆盘空化器的弹体头部产生向下的偏离。这两个因素引起的不平衡力矩，造成弹体在这期间发生一个角速度的阶跃，即忽扑现象。在头部完全沾水后，由于弹体继续前进时攻角为零，水动压力产生的俯仰力矩变为零，因此弹体逐渐恢复之前的入水角度。

入水瞬间空腔和大气相通，所以称之为开空泡。从图6中可以看出，弹体入水形成开空泡，由于水界面空气卷入空泡中，空泡得以持续发展。并且由于入水速度快，弹体表面空泡不易闭合。

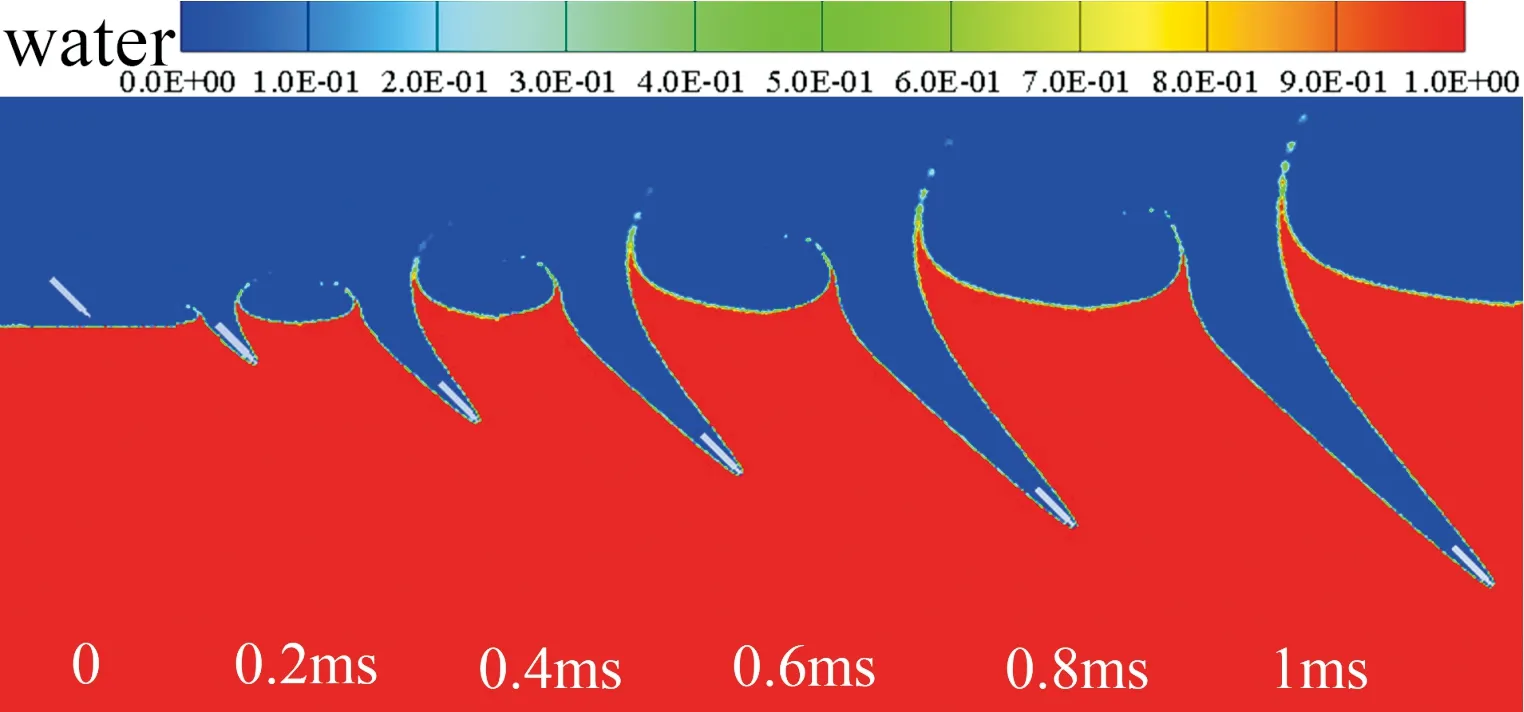
图6 45°入水过程0～1 ms空泡形态变化

图7是弹体不同角度入水0.5 ms时刻头部附近的压力等值线分布图，从图7中可以看出不同入水角度的压力分布趋势是基本一致的，最大压力均集中在弹体头部。

图7 不同角度入水0.5 ms时刻弹体头部的压力等值线图

图8和图9给出了0.5 ms时不同入水角度的空泡形态对比，可以看出，由于倾斜入水过程中弹体对水面的不对称撞击，其产生的喷溅很大部分出现在弹体的水平速度分量正方向。并且空泡右边液面抬升随着入水角度的增加而减小，而空泡左边的液面抬升则增大。这是因为入水角度较大的时候，水平正方向的速度分量较小，在水平前方传递给液体的动能较小，因此右边液面抬升较小；而竖直方向速度分量较大，传递给液体的动能较大，导致了左边液面喷溅较明显，液面抬升较大。

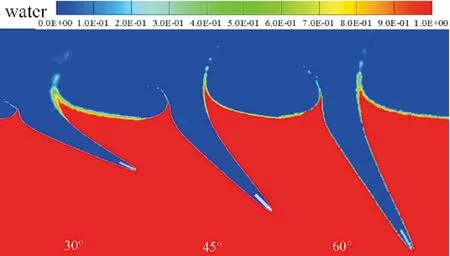
图8 0.5 ms时不同入水角度的空泡云图

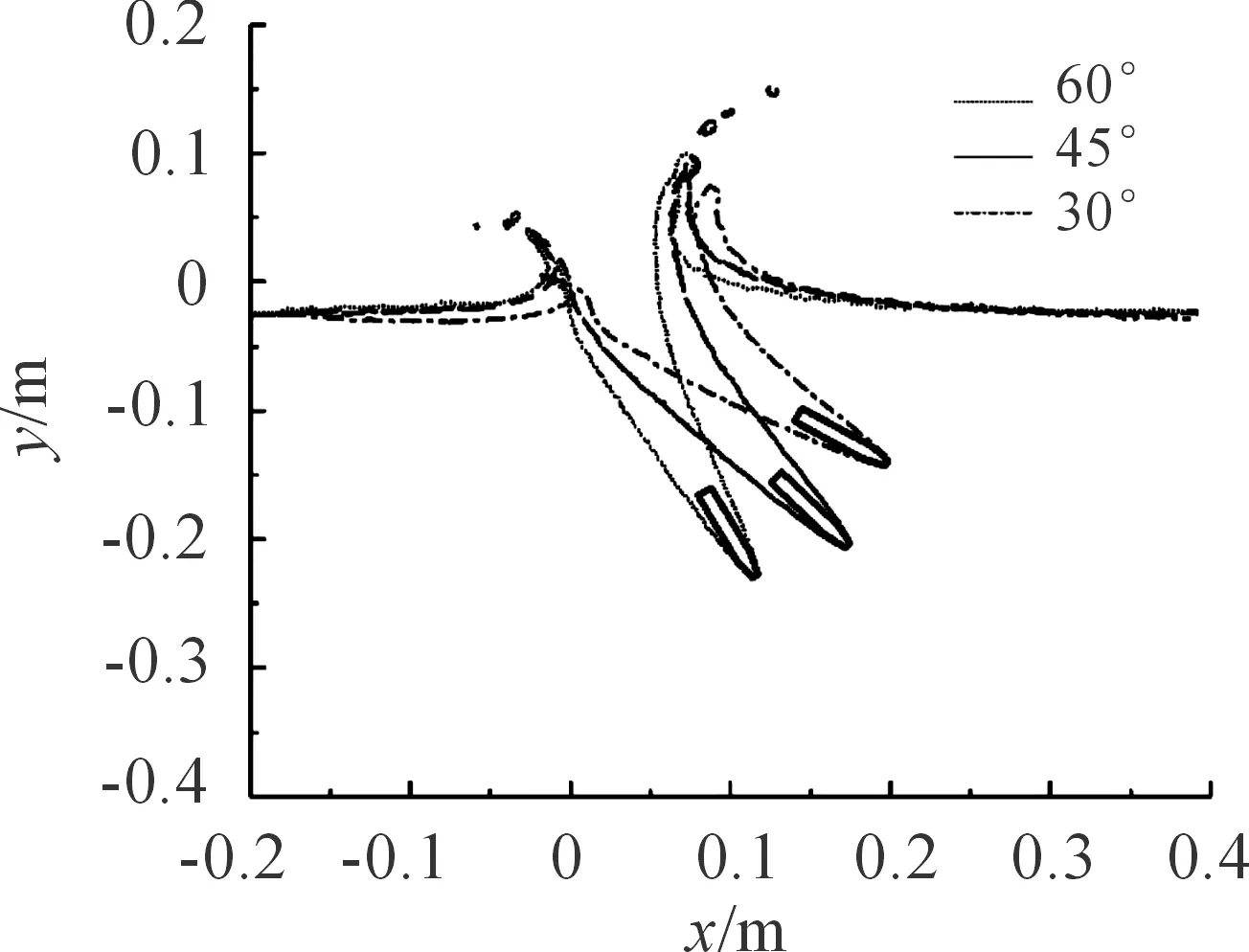
图9 0.5 ms时不同入水角度的空泡形态

4.2 倾斜入水弹道特性及流体动力特性分析

为进一步探究初速度500 m/s弹体以30°、45°和60°3个角度倾斜入水的弹道特性及流体动力特性，对不同入射角度的高速弹体入水进行了数值仿真，仿真结果如图10、图11和图12所示。

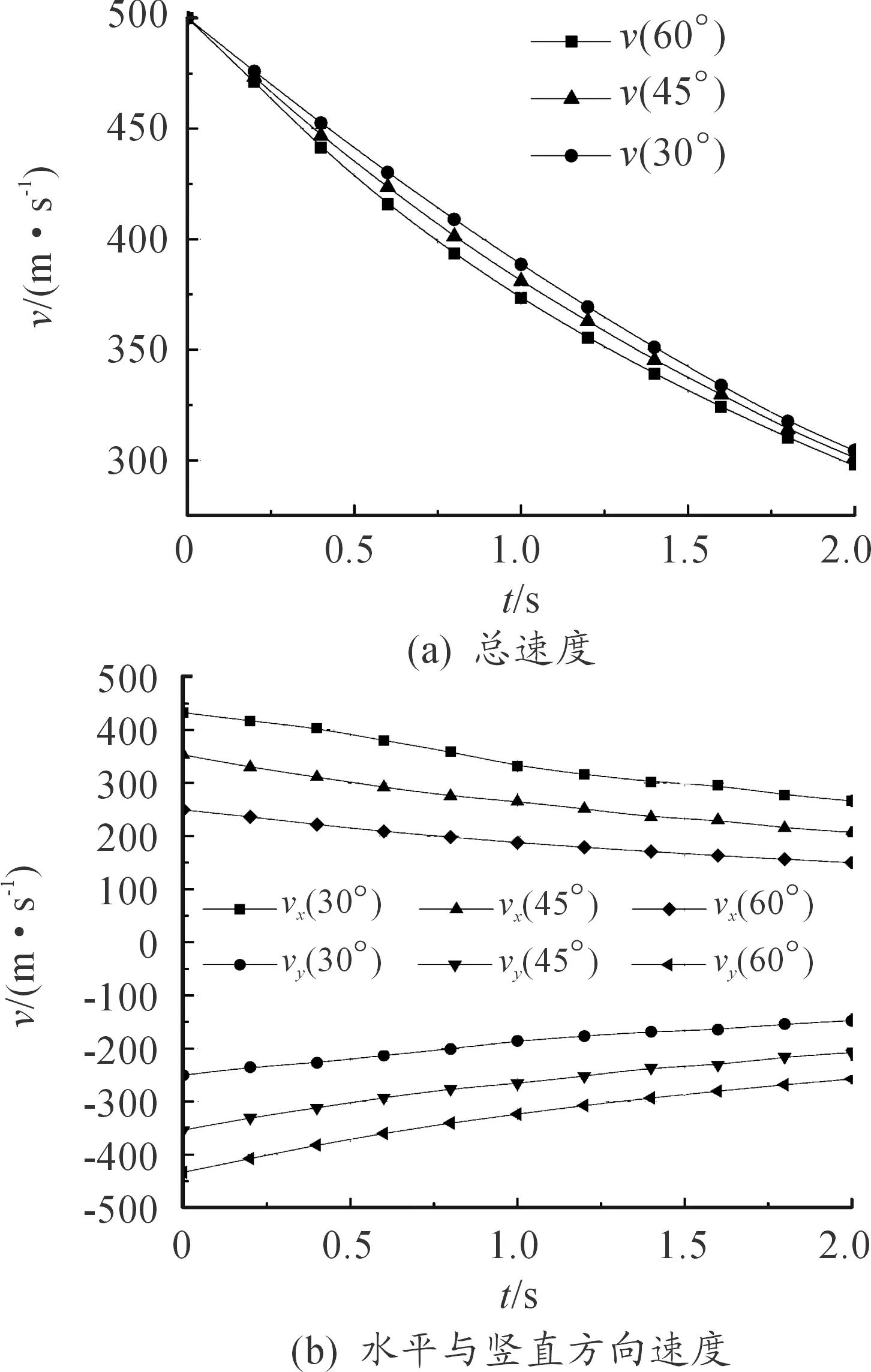
图10 速度衰减曲线

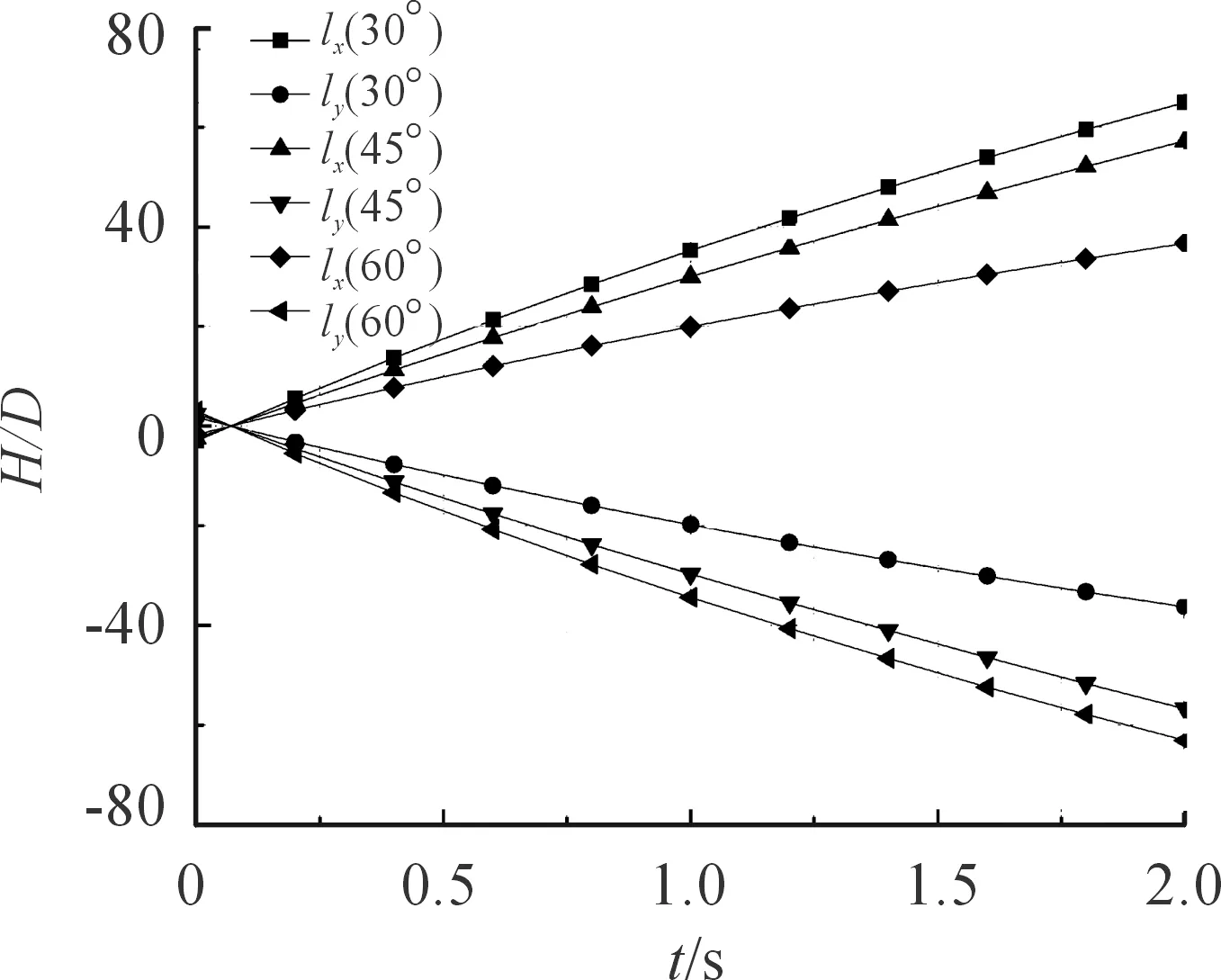
图11 位移变化曲线

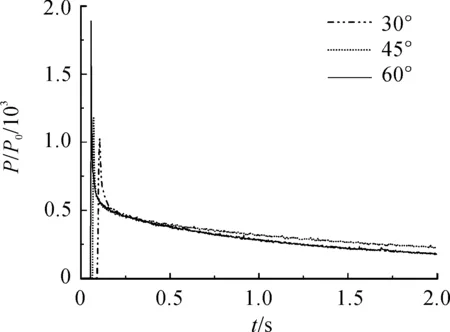
图12 弹体压力变化曲线

图10为不同入水角度射弹总的速度以及重心水平方向、竖直方向速度曲线，观察图10(a)可知，入水角度为60°时，2 ms时间内的速度衰减大于其他两种情况，这是由于入水角度较大时入水瞬间弹体头部的沾湿面积较大，受到了较大的阻力，动能损失较大。图10(b)中高速射弹由于初始运动方向的不同，30°入水角弹体的水平速度衰减速度较60°入水角弹体的衰减速度要快，竖直方向情况则正好相反。总体看来入水角度对总速度的影响不大，这主要是因为弹体在x、y方向受到阻力的合力大致相等。速度衰减曲线的斜率是逐渐减小的，表明弹体受到的阻力在入水瞬间达到最大值，然后逐渐减小。

图11为不同角度入水射弹的水平方向位移lx和竖直方向位移ly曲线。从图11中可以看出，入水角度为30°时，2 ms时间内弹体在水平方向达到最大位移仅仅约为65D，入水角度为60°时，竖直方向有最大位移约60D。这说明弹体在入水瞬间受到了巨大的阻力。同一时刻，入水角度越小，则水平方向位移越大，入水深度越小。

图12为不同角度入水射弹压力变化曲线，由图12可见，在入水之前，弹体受到的压力近似为零，保持恒定；弹体撞击自由液面后在极短时间内其压力出现峰值，此时弹体表面流场压力最高可达大气压的千倍量级。入水角度越大，弹体表面压力峰值越大，且压力衰减速度越快。这是由于入水角度较大时入水瞬间弹体头部的沾湿面积较大，持续受到了较大的阻力。在弹体触水后，随着入水深度的增大，压力峰值逐渐下降，压力数值缓慢减小，逐渐趋于稳定，不同入水角度的弹体压力值差距越来越小，但在2 ms内依然保持较高的水平。