特种弹头结构设计与终点效应研究

孙 银，周克栋，赫 雷

(南京理工大学 机械工程学院， 南京 210094)

由于国际形势瞬息万变，全面的大规模的战争极少爆发，更多的是局部的武装冲突，外交的斡旋，因此各国特种活动大规模出现，对特种作战提出了更高的要求。常见军用武器所使用的枪弹往往采用实心尖弹头，穿透能力大而停止作用不足，在近距离使用时更是能够连穿数人，以致造成误伤。这不能够满足以暗杀、自卫等为目标的特种作战需求。低侵彻、强杀伤的弹头能够满足此类特种作战需求，国内外在役的低侵彻弹如PMC公司的星型露铅空尖弹、雷明顿公司的“金刀弹”、联邦弹药公司的九头蛇弹等都是以满足相关特种作战需求为目标的产品。

创伤力学及终点弹道学等相关学科主要研究内容为弹头侵彻生物体，包括肌肉、内脏以及骨骼等。然而生物组织的冲击实验是非常昂贵甚至是不现实的，在过去的几十年中，明胶作为模拟软组织的材料被广泛地应用于相关实验研究中。Cronin等[1]对明胶材料的应变率和温度敏感性进行了深入研究，测得了10%弹道明胶从低应变率到高应变率(0.01～1 550 s-1)的应力应变特性。Kwon等[2]采用霍普金森压杆实验研究了10%弹道明胶在更高应变率(2 000～3 200 s-1)下的应力应变响应。温垚珂等[3]对4.8 mm钢球、92A手枪弹、SS109步枪弹等侵彻明胶靶标进行了系统性的实验研究，结合理论分析得到了弹头侵彻明胶靶标过程的数值计算模型。曾鑫等[4]对小口径枪弹撞击防护条件下明胶靶标和猪腿时的压力波特性进行了试验研究，发现生物体组织中压力波呈指数衰减。

本文以口径4.5 mm，低侵彻、强杀伤，有效射程8～10 m为设计目标，提出四种典型结构弹头，依据实验结果校验弹头侵彻明胶靶标的有限元模型，在此基础上建立特种弹头侵彻明胶靶标的数值计算模型，对各典型结构特种弹头的侵彻能力进行对比研究。

1 特种弹头结构设计

常规弹头[6]一般由头部，圆柱部，尾部组成。各部分结构和形状均影响弹头的飞行稳定性和致伤效果。设计如图1所示四种结构弹头：尖头弹、钝头弹、非对称弹、头部中空弹。图1(a)为尖头弹，曲率半径和弧形部高度都比较大，弹头比较长。与钝头弹相比，长细比大，质心后移，阻心与质心间的距离较长。图1(b)为钝头弹，多用作手枪弹，与步枪弹相比，初速较低，一般比较短，阻心与质心间的距离较小。图1(c)为非对称弹，本文为研究弹头非对称性对终点效应的影响，将弹头一侧整体圆弧状斜切，整个弹形尖顶偏向一侧。图1(d)为头部中空弹，弹头的结构为圆柱状，口部较薄，容易发生变形和破裂。为降低弹头侵彻能力，提升杀伤性能，弹头采用质地较软的铅作为材料，同时为保证弹头的有效杀伤，采用78 J动能标准作为杀伤判据，弹头打击目标速度为300 m/s。

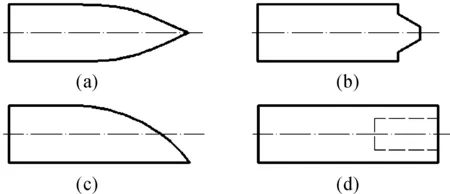
图1 特种弹头结构示意图

2 弹头侵彻明胶靶标模型

明胶材料是一种应变率敏感，温度敏感的材料。本文参照文献[7]的实验，使用9 mm口径parabellum制式弹侵彻明胶靶标实验结果作为校验依据，验证数值计算模型的可行性与准确性。并以计算过程中本构模型、网格匹配等关键仿真参数进行特种弹头的侵彻仿真试验，获取相关参数进行研究。

2.1 弹头侵彻明胶靶标实验模型

弹头侵彻明胶靶标的实验国内外学者已经进行过大量的研究，本文中特种弹的打击目标速度为300 m/s，为保证仿真结果可信度，以文献[7]中的实验过程模型(如图2所示)为参考，枪弹模型尺寸如图3所示，将仿真结果与实验结果进行对比，确认建立的弹头侵彻明胶靶标的数值计算模型的正确性，以此为基础，对特种弹进行数值模拟仿真，获取弹头侵彻明胶靶标过程中的速度变化，靶标内部瞬时空腔、应力云图等参数，进行对比研究。

图2 弹头侵彻明胶靶标实验过程模型

图3 9 mm parabellum枪弹模型

2.2 弹头侵彻明胶靶标有限元模型

建立与实验对应的有限元求解模型，为保证结果一致性和求解效率，建立实体1/2模型，数值计算采用Lagrange算法，使用Solid164实体单元，调整沙漏控制参数使沙漏能在总能量占比不超过10%。弹头与明胶靶标之间接触采用面面侵蚀算法，为防止应力波传递到边界上反弹对仿真结果造成影响，在明胶边界上添加非反射边界条件[8]。网格划分如图4所示，对弹头与明胶直接接触区域的网格进行加密处理，远离接触区域的网格逐渐稀疏[5]。根据实验过程中高速摄影得到的弹头飞行姿态，将弹头向下偏转3°，弹头入射速度为310 m/s。材料本构关系不是本文主要研究内容，因此对弹丸与明胶的材料参数不进行深入研究与探讨，根据文献[5]中仿真模型所使用材料参数进行选取，在软件中进行设置。考虑侵彻过程中弹头变形与应变率效应，弹头使用JOHNSON_COOK材料模型，各参数值如表1[9]。明胶靶标的尺寸为15 cm×15 cm×30 cm，在高动态压力作用下，采用流体弹塑性模型来描述[10]。结合状态方程描述弹道明胶可压缩性影响，状态方程参数值如表2所示[11]。按照文献[7]中进行的实验，实验结果与计算结果如图5所示。

图4 明胶(左)与弹头(右)网格处理

材料ρ/(g·cm-3)G/GPaT/KTm/KA/MPa铅11.3729360014材料B/MPanCm铅17.60.6850.0351.68

表2 明胶状态方程参数值

图5 实验结果(左)与计算结果(右)对比

根据图5，实验中的弹头实际攻角为3°，弹头刚侵彻进入明胶靶标，飞行稳定，明胶内部空腔呈现为锥状，然后不断扩大，随着弹头侵彻深度加大，弹头丧失飞行稳定性，发生偏转与翻滚，内部瞬时空腔为圆柱状。根据仿真结果，250 μs前，弹头飞行稳定，未发生明显偏转，此时明胶内部空腔为锥状，300～700 μs时间段内，弹头发生明显的翻滚，到800 μs时刻，弹头转过90°，此时弹头侵彻深度为20.3 cm，此后，弹头在明胶靶标中翻滚着向前飞行，弹头飞出明胶靶标时的速度为112.4 m/s，弹头侵彻形成的最大瞬时空腔直径为6.2 cm。高速摄影显示780 μs时刻，侵彻深度约为19.5 cm，弹头翻滚角度到达90°，明胶靶标内部最后形成的空腔最大直径为6.4 cm，由于从明胶靶标后部飞出的弹头总是包裹着很多的明胶碎片，弹头飞出明胶的速度无法测量。结合侵彻过程中弹头的飞行姿态、明胶靶标中瞬时空腔的大小与形成趋势，可以看出实验结果与仿真结果一致性较好，本文所建立的有限元模型是有效的。

3 特种弹头侵彻明胶靶标模型

在建立了有效的制式弹侵彻明胶靶标有限元数值模型的基础上，进行特种弹头侵彻明胶靶标的数值仿真实验。

对所设计的四种典型结构特种弹头进行建模，保持明胶靶标模型参数不变，使用1/2模型进行计算。弹头飞行速度为300 m/s，为研究弹头偏转，使弹头有1°攻角，弹头网格示意图如图6(实际计算所使用网格模型经加密处理)，分别导出K文件进行计算，对计算结果进行后处理，记录弹头侵彻过程明胶靶标内部应力云图如图7，特种弹侵彻过程中速度变化曲线如图8，记录弹头翻转90°时侵彻深度与最大瞬时空腔直径如表3所示。

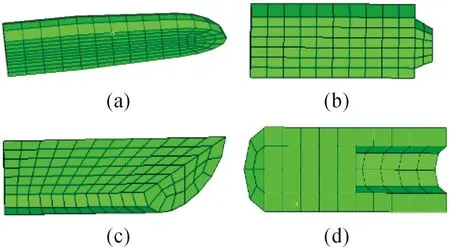
图6 特种弹网格处理示意图

图7 特种弹头侵彻过程云图

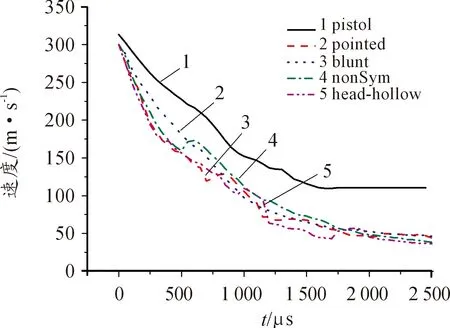
图8 特种弹侵彻过程速度与时间关系曲线

尖头弹钝头弹非对称弹头部中空弹最大瞬时空腔直径/cm3.223.545.354.88翻转90°时侵彻深度/cm17.0718.204.5611.15

从尖头弹侵彻明胶靶标形成的空腔形状可以看出，当弹头刚侵入明胶靶标时飞行稳定，300 μs前，弹头飞行较为稳定，明胶靶标中的瞬时空腔形态类似细长锥体；500～800 μs时间段，弹头发生明显的翻滚，大约950 μs时，弹头的翻滚达到90°，此后弹头在明胶靶标中向前翻滚。

从钝头弹侵彻明胶靶标的空腔形状特点可以看出，瞬时空腔的形成过程与尖头弹类似，起初空腔形状为锥形，当弹头飞行失稳后，空腔逐渐扩展成圆柱状。与尖头弹相比，由于钝头弹头部的受力面积大，锥形空腔部分面积更大，弹头在明胶靶标中的飞行稳定性更好。

从非对称弹头侵彻明胶靶标的空腔形状及应力云图特点可以看出，弹头一侵入明胶靶标，弹头立马发生偏转，靶标中形成巨大的空腔，由于弹头头部几何尺寸较小，结构发生变形伴随着一定的应力集中现象，明胶内部产生更高的应力值。

头部中空弹头侵彻明胶靶标的应力云图与空腔形状和钝头弹有些类似，从入口开始，有一段锥状的空腔，然后扩大，但是由于头部中空弹头口部尺寸较小，弹头发生了大的变形，部分单元失效，弹头几何尺寸不对称，弹头的失稳与翻滚逐渐加剧。200 μs前，弹头飞行较为稳定，整体飞行姿态保持不变，明胶靶标中的瞬时空腔形态类似一个细长的锥体；400～650 μs时间段，弹头发生明显的翻滚运动，大约750 μs时，弹头的翻滚大约为90°，此时刻后弹头在明胶靶标中向前翻滚，且由于弹头变形，与钝头弹相比翻滚更为剧烈。

由于存在射击攻角，侵彻深度达到17 cm左右时，尖头弹、钝头弹在明胶靶标内部弹体旋转达到90°，头部中空弹在侵彻深度达到11.15 cm时翻转达到90°，非对称弹弹头侵入明胶靶标4.56 cm后弹体翻转达到90°。

4 结构参数对终点效应的影响

根据上节计算内容，非对称弹头易于发生偏转，终点弹道稳定性难以保持，实际使用价值低。头部中空弹侵彻能力比尖头弹与钝头弹低，杀伤效能强，与非对称弹头相比，有更好的弹道稳定性，满足设计目标，因此进一步研究头部中空弹头结构参数对终点效应的影响。以头部中空弹头部空心部分长度占弹头总长度百分比为控制参数，进行数值模拟实验，比较空心部分大小对侵彻过程中弹头的速度变化、最大瞬时空腔、弹头在靶标中偏转等参数的影响。

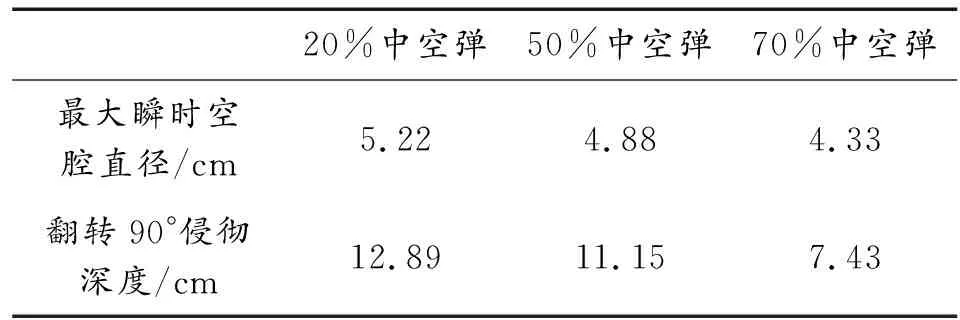
本节所使用计算模型与上节相同，改变头部中空弹空心部分长度，如图9所示，空心部分长度占弹头总长度分别为20%，50%(图6-d)，70%，进行计算与对比分析。记录弹头侵彻过程弹头速度变化如图10所示，记录弹头翻转90°时侵彻深度与最大瞬时空腔直径如表4所示。

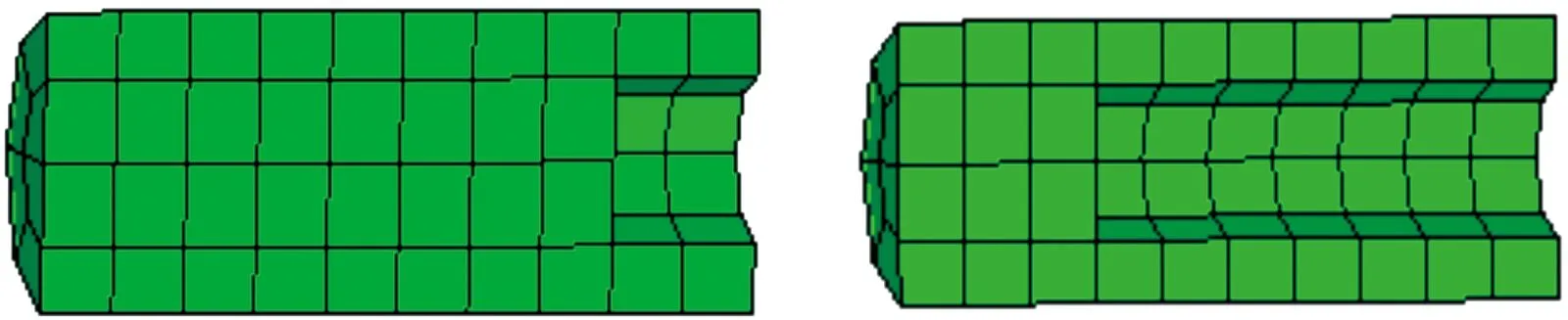
图9 20%头部中空弹(左)与70%头部中空弹(右)

图10 不同中空弹侵彻过程速度与时间关系曲线

20%中空弹50%中空弹70%中空弹最大瞬时空腔直径/cm5.224.884.33翻转90°侵彻深度/cm12.8911.157.43

根据弹头的速度变化曲线可知，弹头进入明胶靶标后速度变化趋势与以上几种弹头类似，均是先快速下降，最终缓慢变为0。其中，70%头部中空弹由于空心部分太长，弹头单元受挤压发生大变形，在 1 700 μs时刻弹头单元全部消失，速度变为0，有限元解释为弹头单元因发生大变形整体失效。根据表4，随着弹头空心部分占比增大，明胶靶标中最大瞬时空腔直径变小，弹头稳定飞行的距离降低。因为弹头头部空心部分增加，弹头受明胶靶标向中心挤压变形，消耗相当一部分能量，同时由于弹头整体质心后移，受到明胶阻力时弹头更易于发生偏转。

5 结论

1) 通过与文献[7]中的实验数据进行对比，验证了建立的弹头侵彻明胶靶标的数值计算模型正确。

2) 通过将所设计的四种典型结构特种弹进行侵彻数值仿真实验，分别得到其终点效应，尖头弹和钝头弹侵彻能力强，飞行稳定性好，非对称弹和头部中空弹侵彻能力低，杀伤性能好。

3) 改变头部中空弹头中空部分所占比，随着弹头空心部分占比增大，头部中空弹侵彻能力降低，杀伤效能降低。

4) 本文所得结论可为低侵彻弹弹头结构设计和采用数值方法研究弹头终点效应提供了借鉴。