基于粒子群优化算法的火箭弹弹道研究

王 捷，田晓丽，贾晓玲，侯 飞

（中北大学机电工程学院，太原030051）

现代战争对于武器装备的要求越来越高。对于导弹和火箭弹这类有火箭发动机的装备而言，射程是一个很重要的指标。目前，比较成熟的增程技术主要有底排增程、火箭增程。底排增程通过减小底阻来提升射程，其射程能提升20%左右。而火箭增程则受限于弹的质量、形状等因素不能无限制装药，使得增程距离也有限。这2种增程技术都难以满足现在对于增程的要求。滑翔增程是通过控制舵翼的偏转，来增大火箭的升阻比来提高射程，是一种比较理想的增程方式。这种方法是基于对火箭弹弹道特性的研究所提出的。弹道特性的研究是弹道修正技术的关键，对分析弹体飞行特点、优化弹道设计、制导控制的设计等有重要的指导意义。以理论计算为基础的数值仿真技术，能够简单、直观地展示弹道飞行特点，为弹道特性的研究提供良好的方法途径[1-2]。通过火箭弹的弹道特性知道，舵翼偏转的角度大小影响着火箭弹的攻角。基于此，本文通过攻角的变化来研究其对于火箭弹射程的影响。

火箭弹飞行过程中，在满足约束条件下达到某些技战术指标的极值，这就是弹道优化设计[3-4]。弹道优化问题是一个动态优化问题，由于其本身的复杂性采用动态优化方法不易求解[5]。因此，需要将弹道优化问题转化为静态的参数优化问题。常用的转换方法有间接法与直接法[6]。直接法是将连续的优化问题直接离散并进行参数化，不需要求解出最优值的条件[7-8]。直接法有直接打靶法、配点法等。间接法是基于极大值原理将最优控制问题转换为哈密顿边值问题。本文采用现代优化算法中的粒子群优化算法对弹道参数优化问题进行研究[9]，充分地证明了现代优化算法应用于弹道优化问题的可行性。

1 模型建立

1.1 火箭弹弹道模型

火箭弹六自由度模型能较精确地解算出弹道诸元，但是在实际运用过程中，六自由度弹道解算复杂，求解时间长，很难满足弹道实时解算的要求[10]。虽然四自由度弹道求解精度不如六自由度，但是它已经能满足落点精度要求，并且其求解时间短，能够满足弹箭弹道实时解算的要求。因此，采用四自由度弹道模型是可行的[11]。

火箭弹四自由度弹道模型如下：

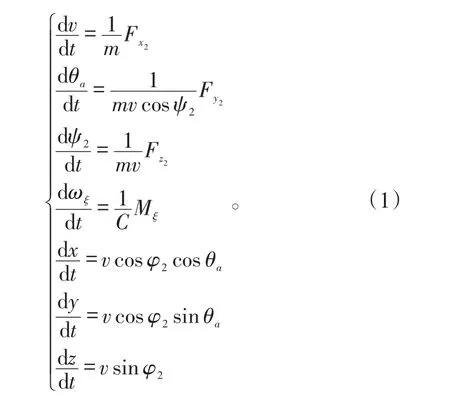
式（1）中，Fx2、Fy2、Fz2为弹箭运动所受力在弹道坐标系上的三分量；m为质量；v为速度；t为时间；θa为速度高低角；φ2为速度方向角；ωξ为弹的滚动角速度；Mξ为弹的滚动运动相关的力矩。

α为攻角，α对于阻力以及升力的大小影响如下：

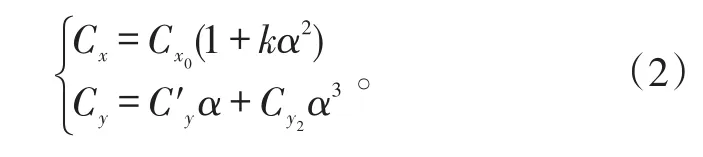
式（2）中：Cx为阻力系数；Cx0为零升阻力系数；Cy为升力系数；C′y为升力系数导数；Cy2为三次升力系数。

对于正常飞行的弹箭，弹轴与速度之间的夹角很小，弹道偏离射击面也很小，本文以攻角为研究对象，所以可设平衡侧滑角β为0。

弹道微分方程的解析解很难求解，通常采用数值解法，即采用龙格库塔法进行求解。

方程组的初始条件为：vx=v0cosα，vy=v0sinα，vz=0，x=0，y=0，z=0。

1.2 粒子群算法优化模型

1.2.1 粒子群算法

粒子群优化算法来源于对简化的社会模型的模拟，是在鸟群、鱼群和人类社会的行为规律的启发下提出的[12-14]。该算法是基于种群进行全局搜索，通过不断迭代逼近最优解[15-17]，收敛速度快，鲁棒性强，近年来多用于轨迹优化[18-19]。粒子群优化算法将每个个体看成搜索空间中的没有体积的粒子，在搜索空间中以一定的速度飞行。粒子的速度及位置分别为：

速度更新公式包含3部分：①粒子先前的速度；②粒子位置向自身历史最佳位置逼近；③粒子位置向群体历史最佳位置逼近。

1.2.2 粒子群算法边界条件处理

当粒子的某一维的速度或者位置超过了预先设定的边界值，采用如下的措施来限制粒子的速度以及位置值。

当v＞vmax或v＜vmin时，

同理，当x＞xmax或x＜xmin时，

式（5）、（6）中：vmin、vmax、xmin、xmax表示预先设定的边界值。

1.2.3 常数的取值

经研究表明：ω的取值在0.8至1.2时，粒子群算法有更好的收敛速度；当ω大于1.2时，粒子群算法易陷入局部收敛。

加速度常数c1和c2分别决定粒子个体经验和群体经验对粒子运动的影响。如果c1和c2均为0，表明粒子的速度只取决于惯性常数ω。此时，粒子的搜索能力有限，很难找到最优解。如果只有c1=0，c2≠0，则该模型只有群体的经验，没有个体的经验，这样该模型收敛速度比较快，但是它比较容易陷入局部极值。如果只有c2=0，c1≠0，则该模型只有个体的经验，而缺乏个体之间的交流，也就是缺乏群体的经验。因此，一般设置c1=c2≠0，这样能保证个体的经验和群体的经验都有相同的权值，如认为个体或整体中某一个更重要，即可设置其加速度常数更大即可。

1.3 粒子群算法优化弹道

1.3.1 目标函数

弹道优化的目标是在火箭弹总体参数已经确定的情况下，使得其射程最远，即：

1.3.2 约束条件

对于某型战斗部的火箭弹，为保证火箭弹的毁伤效果，须对其着速以及着角进行约束。同时，为了保证火箭弹的稳定性，其攻角在一定范围内变化，即：

式（8）中：v是火箭弹的着速；vmax为火箭弹最大着速；θ为火箭弹的着角为负；θmax为火箭弹的最大着角；α为火箭弹的攻角；αmin为火箭弹攻角的最小值；αmax为火箭弹攻角的最大值。

1.3.3 优化变量

火箭弹弹道优化是指火箭弹在飞行中的某个时刻开始，通过控制指令，使舵机产生舵偏从而控制火箭弹的攻角。本文主要研究攻角的变化规律对于火箭弹射程的影响。因此，优化设计变量为攻角，即：

1.3.4 粒子群算法优化弹道流程

1）初始化粒子群，每个粒子的位置以及速度即初始化攻角值，初始化流程如下：

a）从t0到时间内每隔5 s取一个采样点，则采样点个数也是粒子维数D，D=(t-t0)/5+1；

b）初始化群体粒子个数为N；

c）初始化学习因子为c1、c2，惯性权重为ω，最大迭代次数为T；

d）初始化粒子的位置最大值为xmax，最小值为xmin，粒子速度最大值为vmax，粒子速度最小值为vmin；

e）初始化完成后生成了N个粒子，即{N1,N2,…,Nn}。每个粒子的维数为D，某个粒子Ni的初始位置为Ni={αi1,αi2,…,αin} ，并随机初始化粒子Ni的随机速度为vi，即vi={vi1,vi2,…,vin} 。

2）将第1）步得到的N个粒子，代入到弹道模型中，利用龙格库塔法求解出火箭弹的射程R，这也是求解每个粒子的适应度函数值。

3）计算粒子的个体最优值以及整体的最优值即得到当前的最优射程。将上述得到的粒子个体最优值记为Pbest，最优位置记为P，全局最优值记为gbest，局部最优位置记为g。

4）利用式（3）、（4）进行速度、位置更新。

5）进行边界条件判断即判断粒子速度位置知否超出其本身允许的范围，判断方法如下：

判断更新后粒子的速度是否在(vmin,vmax)之间，位置是否在 (vmin,vmax)之间，利用式（5）、（6）进行边界处理。

6）判断是否满足结束条件，即相邻2次射程的差小于某个极小的常数ε，或者迭代次数S大于最大迭代次数T。

若成立则进行第7）步，不成立则返回第2）步。

7）结束运行，输出弹道优化后的各种参数文件。

2 仿真计算结果

结合某型火箭弹的弹道仿真结果，设置粒子群优化算法的各个参数的初始值分别为：t0=0，t=300，D=61，N=100，T=100，ω=0.8，c1=c2=1.5。

对于该型火箭弹，采用初始射击条件分别为：x0=0，y0=0，v0=0，初始射角θ分别为 52°，55°，62°，约束条件vmax=250，θmax=-70°，对其进行优化仿真，所得结果如图1～6所示。

图1为火箭弹飞行过程中攻角为零时的弹道曲线。图2为对火箭弹飞行攻角进行优化后所得到的弹道曲线。图3为未优化的零攻角弹道与优化后的含有攻角的弹道的对比图。图4为采用优化算法优化后的火箭弹的实时攻角。图5为不同初始射角下，经过优化后的弹道曲线图。图6为不同初始射角下，经过优化后的攻角曲线图。

图1 攻角为0时弹道Fig.1 Zero angle of attack trajectory

图2 优化攻角后弹道Fig.2 Optimizing the rear ballistic angle of attack

图3 零攻角弹道与优化弹道Fig.3 Zero angle of attack trajectory and optimal trajectory

图4 优化后的火箭弹的攻角Fig.4 Optimized angle of attack of rocket

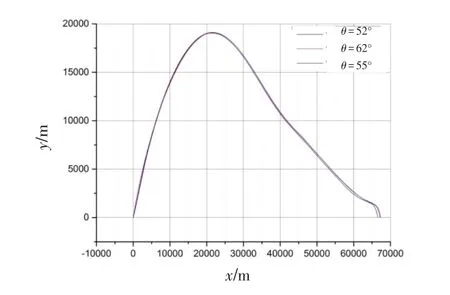
图5 不同射角下的火箭弹弹道Fig.5 Rocket trajectory at different angles of fire

图6 不同射角下攻角曲线Fig.6 Angle of attack curves at different angles of attack

图1～3表明，在52°射角下，攻角为0的火箭弹的射程仅为30.6km，而优化后的火箭弹射程达到66.5km。说明通过控制攻角能有效地增加火箭弹的射程。

图4表明，在火箭弹飞行时间内攻角的变化比较平缓，考虑到攻角的变化是由舵机的舵偏来进行控制的，这样攻角的缓慢变化有利于舵机控制的实现。

图5、6表明，对于不同的初始射角，经过优化仿真后其最大射程基本都在67km附近。并且其对应的攻角曲线图也基本相似，说明对于参数确定的火箭弹，在不同的初始射角下，通过控制攻角可以使其达到最大的射程。

经过优化后的火箭弹弹道参数如表1所示。

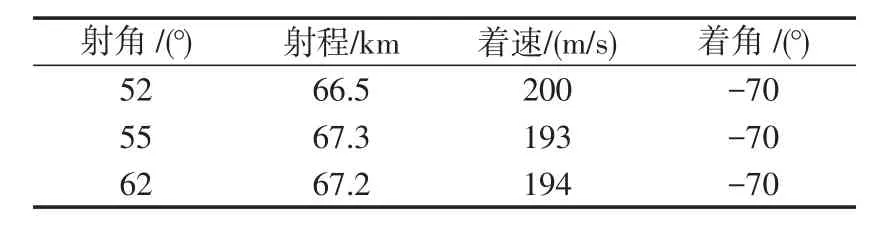
表1 火箭弹落点信息Tab.1 Information of rocket impact point

通过表1可以得到，火箭弹在不同射角下其能达到的最大射程基本一致，并且都满足着速以及着角的约束条件。说明以攻角为变量的优化方案是可行的。

3 结束语

粒子群算法本质上是一种随机搜索算法，它是一种新兴的智能优化技术。该算法能以较大的概率收敛于全局最优解。实践证明，它适合在动态、多目标优化环境中寻优。与传统算法相比，具有较快的计算速度和更好的全局搜索能力。将粒子群优化算法与火箭弹滑翔增程问题进行结合，所得到的结果表明，对应于某型制导火箭弹不同的初始射角，通过控制攻角变化规律都能够达到火箭弹的最大射程。这表明针对火箭弹滑翔增程问题，攻角控制是一个理想的方法。这对于火箭弹射程优化设计有一定的参考价值。