Ginzburg-Landau 方程组弱解的整体吸引子
2019-08-08熊春燕陈淑红
熊春燕, 陈淑红
(闽南师范大学数学与统计学院,福建漳州363000)
本文主要研究Feshbach 共振附近BCS-BEC 跨越中的Ginzburg-Landau 理论:
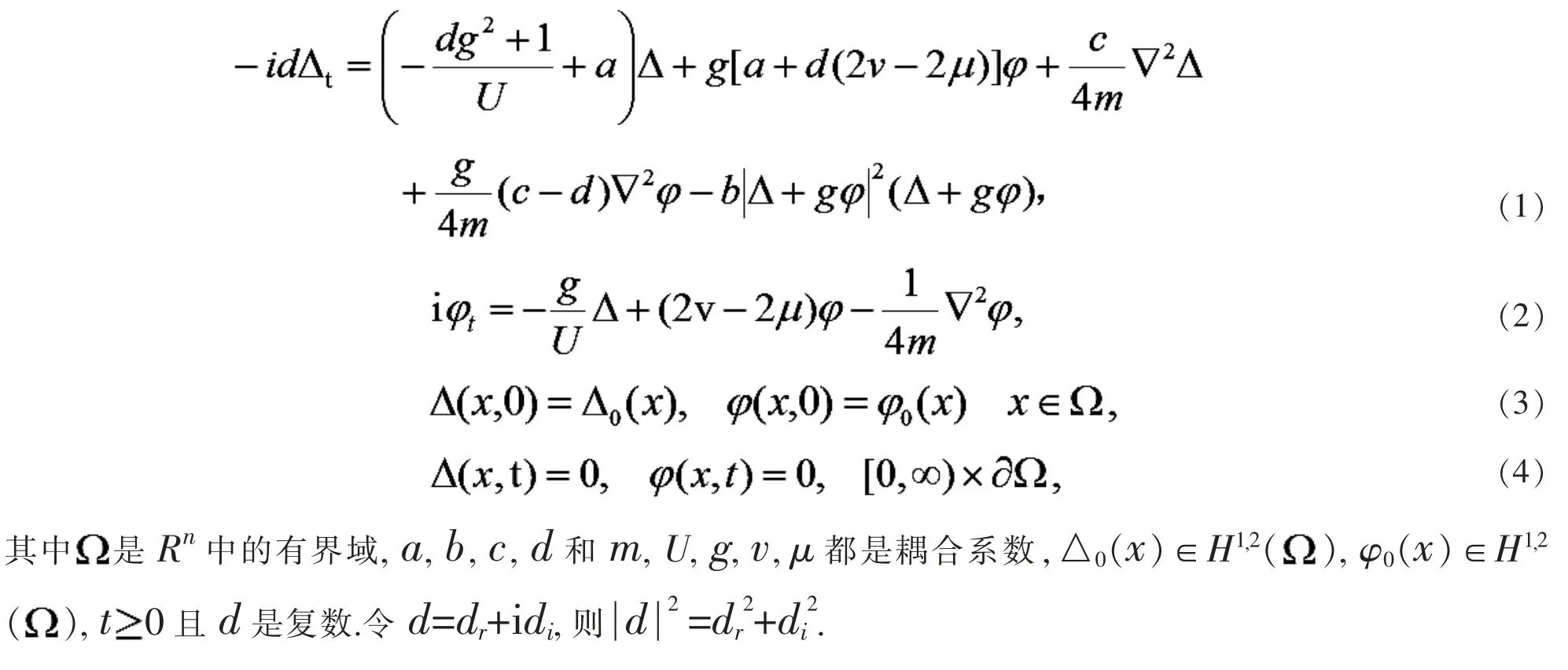
方程组 (1)-(4) 描述的是费米子-玻色子模型中Feshbach 共振附近费米子气体超流中的BCS-BEC跨越现象.
费米子-玻色子模型由于它的特殊性,吸引了广大学者的关注和研究.1987 年,桑建平等[1]对相互作用的玻色子-费米子模型进行了微观研究, 然后给出了与试验符合很好的EU 基态转动态的理论计算谱.1992 年,人们发现了 BCS-BEC 跨越现象,Drechsler M 等[2]和 Sa de Melo C A R 等[3]对费米子-玻色子模型中Feshbach 共振附近费米子气体超流进行研究.Ginzburg-Landau 理论对于费米子气体超流研究起了很重要的作用,黄琨[4]采用路经积分方法建立了描述势阱中的费米子气体在整个BCS-BEC 跨越的不依赖于时间的Ginzburg-Landau 理论.Machida 和Koyama[5]从费米子-玻色子模型出发,对Feshbach 共振附近的超流体费米子气体构造了一个依赖时间的Ginzburg-Landau 理论.证明了与时间相关的Ginzburg-Landau 方程(TDGL)中的耦合系除BEC 极限外是复数.复杂的TDGL 方程既描述了阻尼,又描述了传播动力学,从而在Feshbach 共振附近产生了非常丰富的现象.关于它的数学框架,在BCS-BEC 跨越附近考虑了超流体费米子气体的TDGL 方程.陈淑红[6-8],蓝丽红[9]对该方程组柯西问题、稳态解、古典解及整体解的存在性等进行研究.但该方程组胡整体吸引子未被讨论,故本文考虑研究该方程组弱解的吸引子并得到定理1.
定理1 设(△,φ)为初边值问题(1)-(4)的整体弱解U>0,b0,c>0,m>0,,g>0,且 N=3,△0(x)∈H1,2(), φ0(x)∈H1,2(), 设△+gφ=g1+ig2,φ=φ1+iφ2,则当弱解(△,φ)满足下列三个条件之一时:1)g1=φ1=0; 2)g2=φ2=0; 3),且初边值问题(1)-(4)存在整体吸引子A,且算子A 满足:
(a)StA=A 对于 t∈R+成立;

这里 E=H1,2()×H1,2(),{St,t0}是由方程(1)-(4)产生的半群算子,

1 引理
引理1[10]若函数μ 满足

引理 2[10]若 1<p<∞,对任意函数,有如下等式成立则对边界的外法向量n,,有

2 先验估计
这一部分,我们主要建立初边值问题(1)-(4)的先验估计.首先,我们将方程组(1)-(4)改写为(5)-(8),即

现在我们考虑(5)-(8)式的先验估计.首先,我们来证明弱解的L2-模有界,即

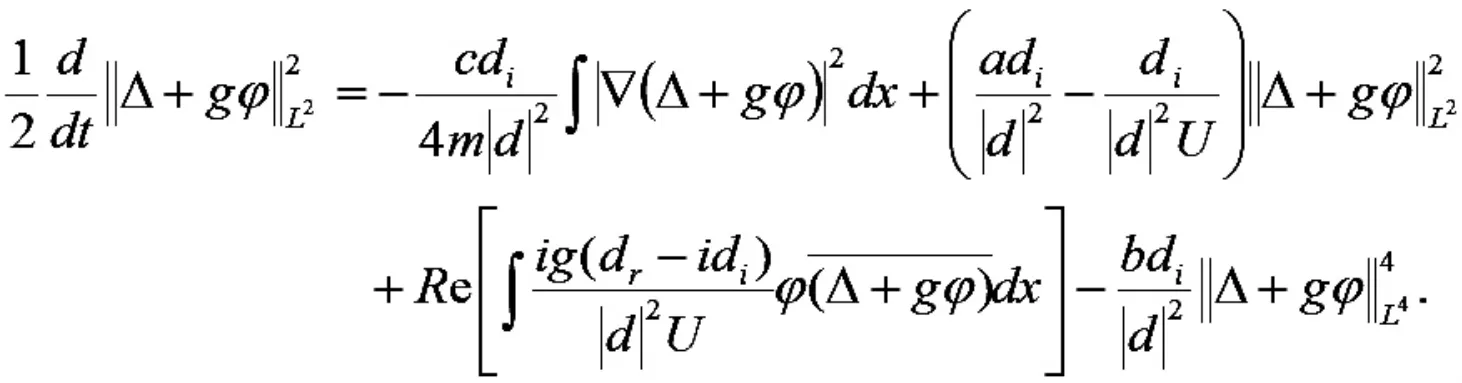
由边值条件(8),poincare'不等式以及Young 不等式得
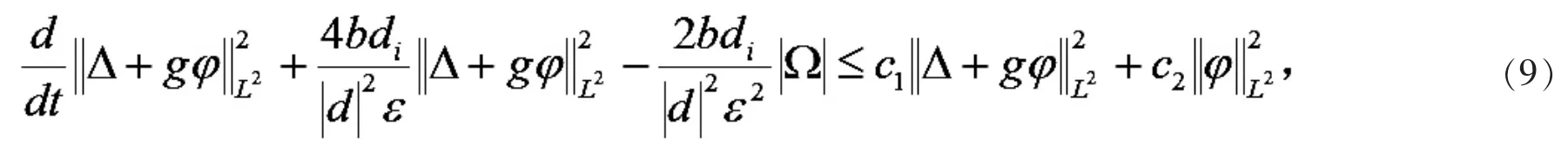
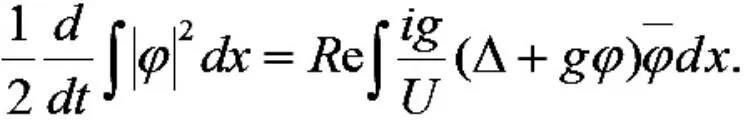
由已知条件和Gronwall 不等式得:


可推出
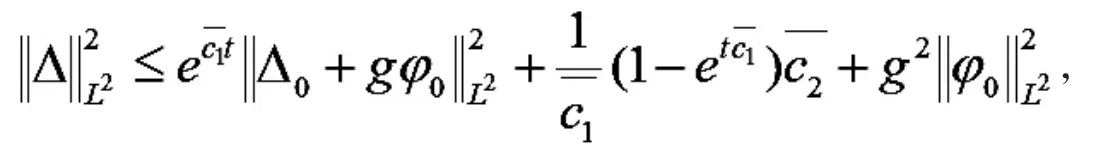
定理3 在定理2 的条件下, 令 poincare' 系数则存在常数 c3<0,c4>0,满足

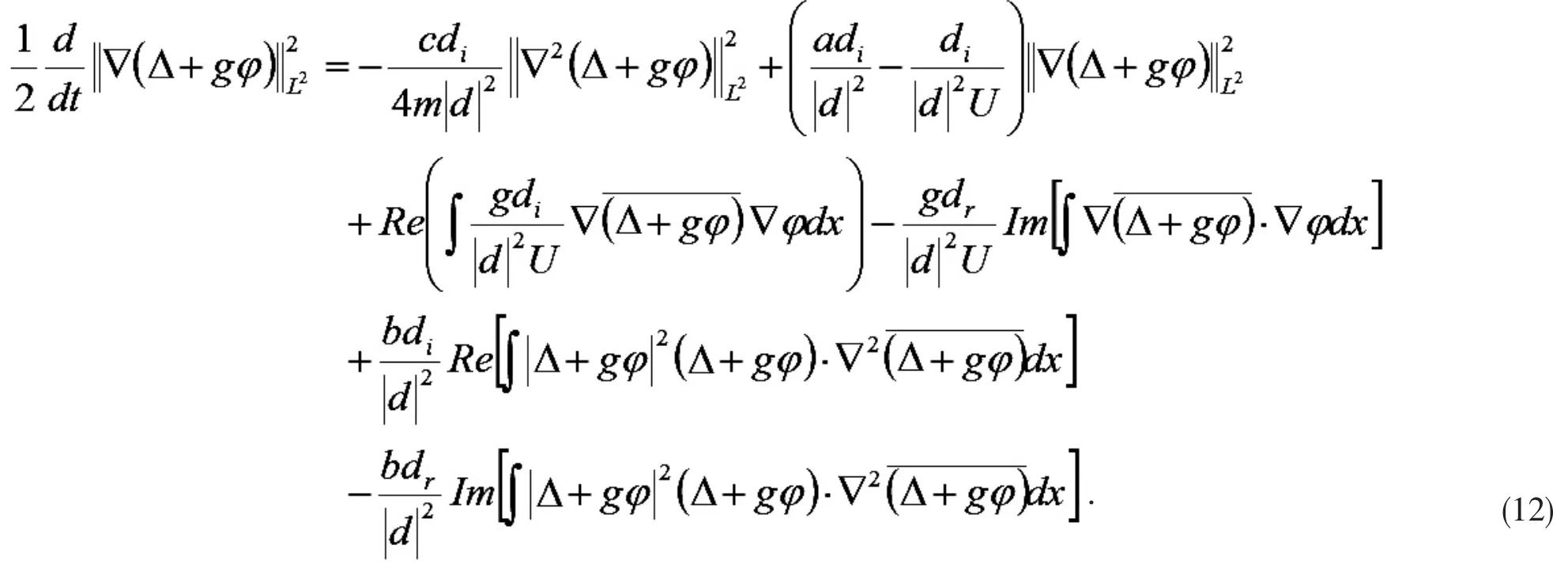

由引理2 可得
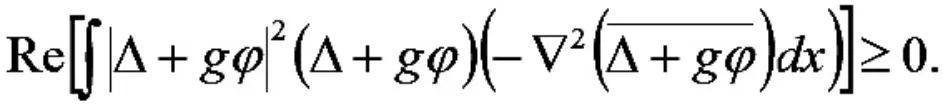
结合(12)(13)式和Young 不等式以及Poincare 不等式,
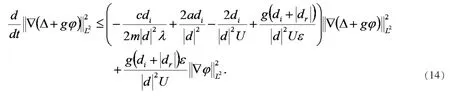

从而(14)可转化为
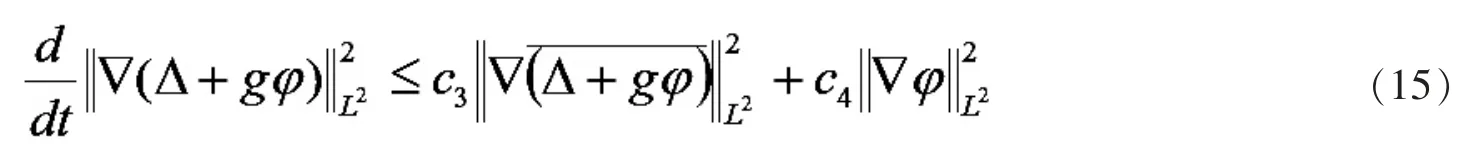

由已知条件和Gronwall 不等式可知

结合(15)(17)可得

由Gronwall 不等式可知

则可推出
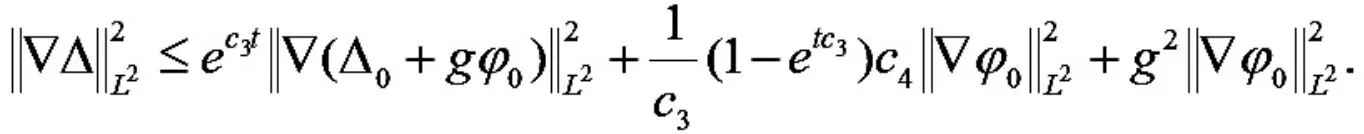
定理4 假设 N=3,在定理3 的条件下,问题(5)-(8)的解满足
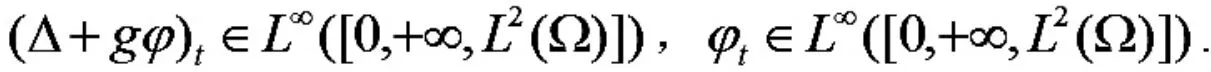
证明 由定理2、3 可得

当N=3 时,利用Sobolev 嵌入定理并结合poincare'不等式,得

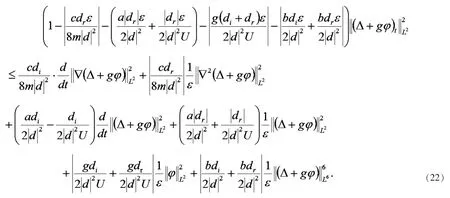
由定理 3 及(20)可知

其中 c11是与 t 无关的常数.
在(22)式中,结合(20)(21)(23)以及定理2 和定理3 的结果取充分小,则
其中 c13是与 t 无关的常数,即

由已知条件和Gronwall 不等式得


3 整体吸引子的存在性
引理 8[11]让 E 是一个 Banach 空间, u 为未知函数,且 u=u(t),{St,t0}是一个半群算子, St:E→E,St·S =St+,S0=I,其中I 为恒等算子,而且半群算子St满足下列条件:
1)半群算子St在E 中一致有界,即对一切R0 存在常数 C(R),使得当时,

2)在E 中存在有界吸收集合B0,即对任意有界吸收集合BE, 存在 T,使得当 tT 时,有 StBB0.
3)当 t>0 时,St为全连续算子,则半群St具有紧的整体吸引子.
最后我们利用引理8,结合定理2-4 证明本文中的主要结论定理1.
定理 1 的证明 在定理 1 的假设条件下,方程满足(1)-(4)存在半群算子{St,t0},因此建立Banach空间且 St:E→E.利用定理2-3 结论并假设BE 属于球可得

其中 K1,K2是常数.意味着St在 E 中一致有界,则引理8 中的条件1)满足.
其次,从定理2-4 的结果,我们可以得到
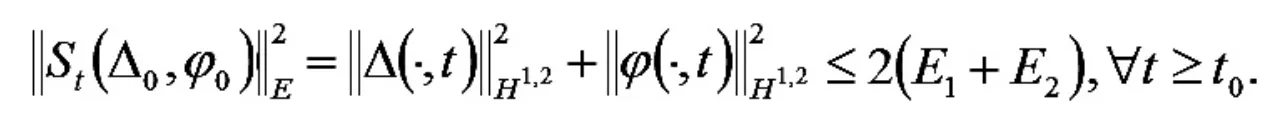
最后,当 t>0 时,
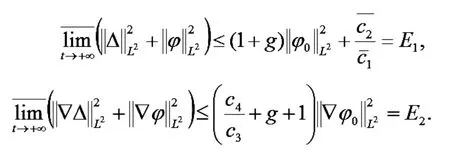
故 t>0 时,St为全连续算子,引理8 中条件3)满足.
综上所述,半群算子St具有紧的整体吸引子定理得证.
