基于数据融合技术的水下油气井计量方法研究

， ，

(1.中石油 克拉玛依石化有限责任公司， 新疆 克拉玛依 834003；2.中国石油大学(北京) 过程流体过滤与分离技术北京市重点实验室， 北京 102249)

随着海洋油气开发走向深海，对其水下生产系统的应用要求也越来越高[1]。在深海生产条件下，若继续使用传统的多相流量计将会使油气田开发成本极大增高，而且其日常维护、校准工作也十分困难。20世纪90年代，虚拟流量计技术被首次提出用于油气田开发，目前该技术在国外油气田开发中应用较为广泛。我国自主研发的首个海上凝析气田虚拟流量计系统[2-3]已于2014年在我国南海投入使用，该系统依托多相流模拟技术，根据油气田提供的工艺参数和生产数据，通过计算机及相应的软件实时计算所需的流动信息，从而提供相应的油气田管理对策。但该虚拟流量计系统在投产运行期间产生了部分时间段精度不高、可靠性低的问题。针对此情况，基于数据融合的思想，分别采用D-S证据理论、不确定度理论及神经网络理论，设计了基于多个物理流量模型计算结果的3种数据融合流量估计算法，该算法能极大降低由于单个物理模型结果偏差过大而对整个流量计系统造成的影响，从而有效提高虚拟流量计系统的可靠性、稳定性和精度。

1 数据融合技术

数据融合技术最早出现在20世纪70年代，经过近40 a的发展，该技术已被广泛应用于多源图像合成、智能系统、目标跟踪及多相流等领域[4-6]。数据融合的基本原理源自于人脑对信息的处理方式，通过神经中枢将感受到的信息传送到大脑进行综合处理，然后再对外部环境进行判断和控制[4]。数据融合能够充分利用多个传感器在不同空间或时间采集到的可融合或者互补的数据资源，采用计算机技术，对多个传感器获得的数据，在特定的准则或算法下进行分析、组合、计算，以获得对被测对象的一致性解释或描述，从而实现相应的决策与估计，使系统获得比单一数据源更可靠、更准确的信息[7]。

常用的数据融合方法主要包括加权平均、卡尔曼滤波、贝叶斯估计、D-S证据理论、模糊推理及神经网络等，各方法的特点见表1。

表1 各种数据融合方法特点

每个物理流量模型的计算精度不同，且当某个模型失效时，虚拟流量计系统的可靠性和精度必定会受到影响。为了保证计量的精度和可靠性，根据虚拟流量计系统对计算速度和计算精度的要求，利用数据融合技术设计了加权平均、D-S证据理论和神经网络这3种数据融合算法进行流量估计。

2 物理流量模型

2.1 水下凝析气田流动系统

典型的水下凝析气田流动系统示意图见图1。由图1可知，流体从井底至平台分离器的流动存在井筒、油嘴及跨接管的多相流动节点。根据流体在管段不同节点间的多相流动过程，利用各节点的温度、压力及沿线基本参数，分别建立了用于单井流量计量的井筒、油嘴、筒嘴及跨接管等物理模型。

图1 典型的水下凝析气田流动系统示图

2.2 井筒模型

井筒模型是根据流体在井筒中的多相流动过程，利用能量、动量及连续性方程描述井筒稳态流动的算法，给出单井流量的上下限范围，并根据井底、井口的压力、温度实测值，利用二分法迭代求解出单井质量流量，具体求解过程见文献[8-9]。

2.3 油嘴模型

油嘴模型是利用多相流体流过油嘴阀门的流动特性而建立的流量预测算法。文中主要利用Schüller等[10]推导的油嘴模型进行凝析气井单井流量的计算，应用该模型时需要对油嘴的流量系数进行定期修正。

2.4 筒嘴模型

筒嘴模型实质是井筒模型和油嘴模型的结合，其将多相流体在井筒和油嘴中的流动过程作为一个整体来考虑，利用井底和油嘴后的温度、压力求解得到流量。

2.5 跨接管模型

跨接管的特点是长度短、压降小且降温大。利用流体在跨接管中的稳态热力算法，根据跨接管的一段温度、压力和管汇处的温度便可求解得到流量数值[11]。

3 基于数据融合技术的油气井流量算法

3.1 基于D-S证据理论

基于D-S证据理论的多模型融合算法是D-S证据理论与加权融合的结合，根据各个物理流量模型的结果，由D-S证据理论合成法则来确定各物理流量模型的融合权重，然后进行加权融合，具体方法见文献[11-12]。

3.2 基于不确定度理论

基于不确定度理论的多模型融合算法也是利用加权融合，不同之处在于各模型的权重是根据虚拟流量计系统各模型的不确定度大小来确定的。根据JJF 1059.1—2012《测量不确定度评定与表示》[13]，测量不确定度的定义为根据所用到的信息，表征赋予被测量分散性的非负参数。测量不确定度一般由若干分量组成，每个分量用其概率分布的标准偏差估计值表征，称为标准不确定度。标准不确定度的评定方法包括A类评定和B类评定。A类评定是在规定条件下对测得的量值用统计分析的方法进行测量不确定度的分量评定。B类评定是根据有关的信息或经验，判断被测量的可能值区间。当被测量估计值y由N个其他量x1，x2，…xN通过测量函数f确定时，被测量的估计值y=f(x1，x2，…xN)，被测量估计值y的合成标准不确定度uc(y)按以下公式计算：

(1)

式中，y为被测量的估计值；xi为输入量的估计值；∂f/∂xi为灵敏系数，为被测量与相关输入量之间的函数；对于输入量xi的偏导数，文中取1；u(xi)为输入量的标准不确定度。

基于上述不确定度理论，对于虚拟流量计系统不确定度的来源主要考虑沿线各仪表的不确定度和物理流量模型的不确定度两部分。其中仪表部分的不确定度根据B类评定方法确定，该部分的不确定度一经确定，便认为其不再发生改变。各物理流量模型的不确定度根据其计算结果利用A类评定方法确定，这就要求在进行不确定度计算时，实际的流量数据在小范围内波动或者基本维持不变，否则评价结果将失去意义。物理流量模型的不确定度会随着计算结果准确性的变化而发生改变。在确定仪表不确定度和物理流量模型不确定度后，便可对这两部分进行合成得到合成后的不确定度：

(2)

在进行加权融合时，各模型的权重为：

(3)

基于不确定度理论的多模型融合结果为：

(4)

式中，Wi为单个物理流量模型的流量计算结果，n为物理流量模型的个数。

3.3 基于神经网络

人工神经网络具有高度的并行性、较强的容错能力及非线性自适应能力等优点[14]，是一种良好的数据融合方法。在当前人工神经网络实际应用中，80%～90%的人工神经网络模型都是采用BP前馈网络或其变形形式。多模型融合反映的各模型数据间的关系很复杂，非线性模式也多种多样，多层前馈网络能将各物理模型的计算结果作为输入非线性组合进行建模，若给定足够的隐藏神经元，它可以逼近任何函数。BP神经网络的学习采用误差反向传播算法，其把整个学习过程分为2个阶段，第1阶段为正向传播过程，训练样本从输入层输入，经过隐含层处理后传向输出层。若在输出层未得到期望的输出，则进入第2阶段，即误差的反向传播阶段，将输出层的误差以某种形式通过隐含层向输入层反传，并将误差分配给各层的所有单元，从而获得各层单元的误差信号并将其作为修正各单元权重的依据。这2个阶段相互交替反复进行，不断调整网络各单元的权值，直到网络的输出值误差达到要求的标准或预先设定的学习次数为止。

本文采用BP神经网络的输入层单元有4个，分别为各物理流量模型的计算结果，输出层单元有1个，为融合后的流量计算值。基于BP神经网络的数据融合算法流量估计过程见图2。

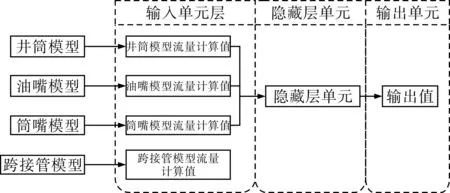
图2 基于BP神经网络的数据融合算法流量估计过程

将基于神经网络的多模型数据融合方法运用在油气井的流量估计中，是为了得到下一时刻更加准确、可靠的单井流量值。在线应用时，数据点较多，为了减小计算量，建议采用时间滚动的训练样本学习方法[15]，即随着时间的推移，训练集逐渐舍弃距离当前时间点较远的数据，保持样本数量始终维持在一个较小的范围内却又能反映当前时间段内流量的变化情况。

4 基于数据融合技术的油气井流量算法应用实例分析

利用虚拟流量计系统在我国南海某凝析气井投产应用时收集到的2015-02～2015-07的生产流量数据对各模型的算法进行验证，并对计算结果进行分析。

4.1 各物理流量模型均正常运行

在单个物理流量模型均正常运行，没有异常情况发生时，各物理流量模型及融合算法的计算结果与实测值对比见图3，各物理流量模型计算结果的平均绝对百分比误差见图4。

图3 2015年正常工况下各物理流量模型预测结果与实测值对比

图4 2015年正常工况下各物理流量模型计算结果平均绝对百分比误差

由图4可以知道，井筒模型计算结果的平均绝对百分比误差仅为0.042，是所有物理流量模型中最小的，说明在当前时间段内各物理流量模型中，井筒模型的整体计算精度最高，波动性最小，最接近实际工况。

在各种融合算法中，基于BP神经网络的数据融合流量预测结果的平均绝对百分比误差仅为0.039，结果优于井筒模型及其他2种融合算法，这主要是由于人工神经网络具有高度非线性自适应性的优点，但该融合算法整体计算速度较慢。基于D-S证据理论和不确定度理论的多模型数据融合算法计算结果的平均绝对百分比误差比井筒模型的稍大，但小于其他物理流量模型的。这主要是由于在加权融合算法中，精度较低的物理流量模型占据了一部分比例所造成的，但从整体看，2种融合算法与井筒模型的平均绝对百分比误差相差不到0.005，说明融合流量技术更加贴近实际情况，计算结果的精度能与最优物理流量模型相当。

4.2 井筒模型异常工况

井筒模型的计算结果在各物理流量模型中最优，如果井筒模型出现异常，对融合流量算法的结果影响最大。为了验证某物理流量模型运行异常或失效对各融合流量预测技术的影响，假设2015-02-27～2015-03-11井筒模型的流量预测值比实际偏小30%，其他物理流量模型结果保持不变，得到的各模型及融合流量算法计算结果见图5，平均绝对百分比误差见图6。

图5 2015年井筒部分时间段异常工况下各物理流量模型预测结果与实测值对比

图6 2015年井筒部分时间段异常工况下各物理流量模型计算结果平均绝对百分比误差

由图6可知，在井筒模型部分时间段发生异常工况下，井筒模型计算结果的平均绝对百分比误差增加至0.079，在所有物理流量模型中，油嘴模型计算结果的平均绝对百分比误差最小。从各数据融合流量算法的结果看，基于BP神经网络的数据融合流量算法的平均绝对百分比误差为0.041，相比其他2种数据融合流量算法整体结果仍是最优。基于D-S证据理论和不确定度理论的多模型数据融合算法的计算结果稍次于基于BP神经网络的多模型算法，但均优于油嘴模型。其中基于不确定度理论的多模型数据融合算法平均绝对百分比误差比油嘴模型小2%，精度与稳定性均较好。说明在某物理流量模型异常的情况下，多模型数据融合算法相比单个物理流量模型仍能保证较高的可靠性和精度，达到算法最初的设计要求。

在3种数据融合算法中，基于BP神经网络的融合流量预测方法虽然精度最高，但是计算速度比较慢；基于D-S证据理论和不确定度理论的数据融合算法精度稍低，但是计算速度比较快。在实际应用时，可以根据应用要求选择其中的1种或者2种数据融合算法。

5 结语

基于数据融合技术，设计了3种用于水下油气井生产计量虚拟流量计系统的融合流量预测算法，现场测试结果表明，采用融合流量算法得到的计算结果的平均误差维持在5%以内，整体上比基于多相流模拟技术的物理流量模型小3%，所估计的流量更贴近实际工况。在某个物理流量模型失效的情况下，数据融合流量技术仍能给出比当前最优物理流量模型更加精确的流量预测结果，极大降低了单个物理流量模型异常对虚拟流量计系统计量结果的影响，有效保证了整个系统在线应用时的可靠性、稳定性和精度。