从一道课本例题谈学生“知识建构”和“数学素养”——“模块融合”教学实验有效性探究

广东省广州市铁一中学(510600) 韩晓雪

一、“模块融合”教学实验背景介绍

“模块融合”是笔者所在课题组进行的一项初中数学课堂教学实验.该实验尝试将初中数学知识进行“模块”划分，然后通过教材重组实现模块间的融合.该教学实验突出表现在将函数作为初中代数部分的敲门砖，将函数和一次函数的内容拆分成几部分，分别放入七年级“代数式”“一元一次方程”“二元一次方程组”和“一元一次不等式”章节中，实现在七年级进行函数模块的知识螺旋上升，同时利用函数知识引入方程、不等式概念，并利用函数图像的数形结合性解决方程、不等式的相关问题.类似的在八九年级实现分式方程和反比例函数、一元二次方程和二次函数的模块融合.该教学实验旨在融合，通过教材重组的课堂教学实验更有效的实现学生知识系统建构，培养学生“数学素养”.

二、课本例题常规教学困难分析

笔者在进行“一次函数与一元一次不等式”章节的讲义编写过程中，参考了新人教版七年级(下)第九章《一元一次不等式(组)》的教材内容.在教材的重组过程中关注到课本的一道例题：甲、乙两家商场以相同的价格出售同样的商品，并且又各自推出不同的优惠方案：在甲商场累计购物超过100 元后，超出100 元的部分按90%收费;在乙商场累计购物超过50 元后，超出50 元的部分按95%收费．顾客到哪家商场购物花费少?

该例题出现在9.2.2 实际问题与一元一次不等式中，可以说是一道课堂教学中非常头疼的题目，其主要困难表现在与学生的既有知识系统和解题能力不匹配.众多教师反应，该例题在中等程度班级教学中，往往要耗费大量时间，最终教学效果仅停留于理解题目解答，而不能掌握方法更难以灵活运用于它题.在教师引导学生思考的过程中，其思维障碍有以下几点：1、题目条件过于繁琐，题目中虽然只出现4 个数据，但隶属两个不同方案，而且每种方案都有一次分段，造成学生读题困难.2、问题提问方式开放，一般题目都是问一个量的多少，而这道题问到哪家商场购物花费少，不少学生根本不知道该将什么量进行比较，从而无从下手.3、题目涉及双重分类，第一重分类为什么要把消费50 元和100 元作为分类的截点，第二重分类为什么要比较两店花费的三种情况，这两个重要问题是这道例题的解题关键，但即使老师合理引导，也会有很大一部分学生无法自主探究得到.以上困难究其原因是教材设计的不合理，在一元一次不等式的解法刚刚结束，没有任何铺垫和引导，突然出现一道如此难度的实际问题，就好像在学生面前突然立起一道陡峭的山梁，而又没有给予合理的攀爬路径.

三、“模块融合”教学实验设计及课堂呈现

(一) 教学实验设计

针对以上分析的课堂教学困难，笔者在进行讲义编写时，结合“模块融合”的理念，对本章教材作出以下调整：

调整1 类似于“一元一次方程”和“二元一次方程组”，用函数引入“一元一次不等式”概念.例如：引导学生从函数y=0.3x+6 得到不等式0.3x+6＜7.5.

调整2 在《实际问题与一元一次不等式》这一节课中，自行设计了两道例题，一道为简单不等式的应用，一道为简单的方案选择问题.

调整3 在实际问题后设计融合课程《一次函数与一元一次不等式》.例如：某电信局收取网费如下：A 网费为每小时3 元;B 网费为每小时2 元，但要收取每月基本费15 元．设每月上网总费用为y(单位：元)，上网时间为x(单位：时)．分别求两种上网方式中y与x的函数关系式.若选择B 网费模式，则上网时间x满足什么条件才合算?A：y1=3x;B：y2=2x+15，显然x≥0，这里涉及两个一次函数，我们在同一坐标系中做出图像如图1.在图像上我们可以发现，当x=15 时，y1=y2=45，两图像交于一点.而要求B 网费模式更合算，即y1＞y2，则对应图像右上段，y2=2x+15 的图像位于y1=3x的图像的下方，即交点(15,45)的右侧图像范围，因此得到此时x＞15.

图1

调整4 给出上文涉及的“甲乙商场选择”问题，并且由教师指引学生发现——提出——解决问题三步走.下文课堂呈现会具体论述.

(二)“甲乙商场选择”问题课堂呈现

该实验课程由课题组中七年级教师在实验班操作完成，笔者作为听课教师参与并记录了该问题在课堂中的呈现情况.

环节1 分小组讨论题目条件，自行提出与解题有关的问题.通过学生有序讨论并发言，总结出以下关键问题：问题1：若要作比较，那在两家商场的花费与哪个量有关? 问题2：如果原购物款为x元，能得到两家商场的花费与x之间的函数吗? 问题3：如何比较这两个函数的大小?

环节2 学生独立思考，逐一解决以上问题，并展示题目解答.部分学生基于《实际问题与一元一次不等式》中的已学过的简单方案选择问题，提出与上文教材解答方法一致的过程.在教师巡视课堂中也发现了不少学生采用函数方法解答，并邀请一位学生展示，其基本思路如下：

把富集培养液进行梯度稀释，并涂布于无机盐培养基平板，挑取10株单菌落划线纯化，并接入无机盐液体培养基中，30℃静置培养15 d，0.2 μm滤膜过滤，取滤液进行气相色谱检测[6]。

(1) 当累计购物不超过50 元，两商场一样;

(2) 超过50 元而不超过100 元时，明显选乙;

(3) 超过100 元时，设累计购物x元(x＞100).可得甲商场：y1=100+0.9(x-100)=0.9x+10，乙商场：y2=50+0.95(x-50)=0.95x+2.5.分别计算x=100和x=200 时的函数值，做出两个一次函数图像，如图2是学生课堂所做草图.

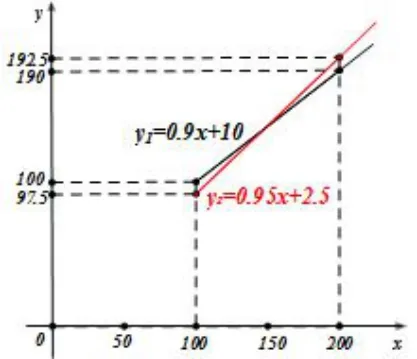
图2

通过图像发现，当x＞100 时有交点，在交点两侧呈现不同的大小关系，因此利用0.9x+10=0.95x+2.5 求两函数交点(150,145)，由图像可得当x=150 时，y1=y2=145，此时两家商场一样，当x ＜150 时，y1＞y2，此时乙商场更便宜，当x＞150 时，y1＜y2，此时甲商场更便宜.

该方法利用函数图像清晰明快的解决了为什么在消费超过100 元时要分类得出三种选择.利用函数的数形结合性直观展示了代数实际问题的思维难点，提示了分类的必要性.

环节3 思维拔高，学生提出新解答.在老师肯定了环节2 中学生的方法后，有学生提出另一种全新的思考方法，他说既然我们用函数图像清晰的显示了超过100 元后两商场消费的情况，那能否把前两种情况也都直观的表示出来呢? 于是在教师的带领下，学生们思考上述问题，并做出以下解答：设累计购物x元.可得甲商场：当x≤ 100 时，y1=x; 当x＞100 时，y1=100+0.9(x-100)=0.9x+10;乙商场：当x≤50 时，y2=x;当x＞50 时，y2=50+0.95(x-50)=0.95x+2.5.在同一坐标系做出图像，如图3为课堂上学生所做草图.

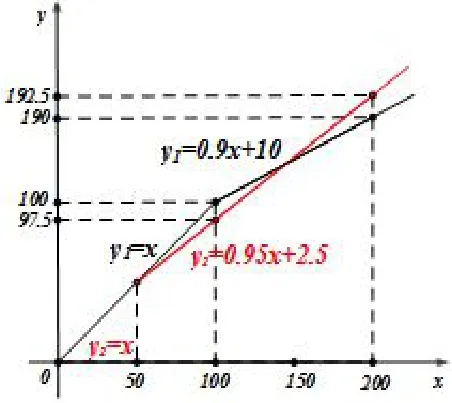
图3

两函数图像有一段重叠，是当0＜x≤50 时，此时甲乙两商场一样; 由上一环节的学生解法可知，两函数图像有另一交点，为(150,145)，由图像可得：当x=150 时，y1=y2=145，此时两家商场一样;当x ＜150 时，y1＞y2，此时乙商场更便宜;当x＞150 时，y1＜y2，此时甲商场更便宜.

对于学生有这样的思维碰撞，产生这样的解答，教师给予了表扬，也同时关于该题做出总结：方案选择实际上是两个不同函数之间的大小比较，那么只要先弄清楚这两个函数是什么，再比较就简洁明了，而函数图像是比较大小的直观展现，也许我们未来遇到的问题会更复杂，但利用函数解决这类方案选择问题都不失为一种好方法.

四、结合上例的“模块融合”有效性探究

(一)“模块融合”促进学生自主“知识建构”

从知识系统角度上，数学知识既是离散的，又是连续的.如何将离散的数学知识变成连续的知识链，是教材开发和教学实践的重要目标.基于教学内容和难度螺旋上升，也基于学生数学学习的获得感，我们不能刻意的将同一知识链的内容强行安排在一起.而“模块融合”的教学实践，着眼于知识链中的“链”，合理安排课程和教学，更有利于学生知识链的形成.

在上例中，笔者在进行教材蓝本运用过程中，调整1 中函数引入设计，合理设计实践问题，把函数和不等式有效整合，打破概念之间的隔阂，引导学生用函数的角度理解不等式，在学生知识系统有机的建立起两者之间的联系;调整2中，先不讨论上文涉及的“甲乙商场选择”问题，而是自行设计了两道例题，让学生从易到难接触一元一次不等式在实际问题中的应用，特别是用函数的角度理解不等式的应用，从函数图象角度观察不等式的解集范围，形成一定的解题能力基础，实现从认识到理解应用的能力升华.调整3 中，增加一个课时，为融合课程《一次函数与一元一次不等式》，在其中进行例题设计，比如上文提及的网费选择问题，较之“甲乙商场选择”问题函数更简单，图象更清晰，学生更易理解和运用，帮助学生从函数图像角度深化一次函数与一元一次不等式的关系，实现代数知识的几何内化.基于以上设计，完成融合课程后，给出上文涉及的“甲乙商场选择”问题.学生经历之前的融合建构知识系统过程，在已有的知识和方法基础上，解决这一问题就变得不是那么困难了.

“模块融合”教学实践在课程设置中，进行了知识内容的调整，同一模块按知识建构顺序排列，形成一条知识链，有利于学生的纵向知识架构.同时不同章节采用类似的引入探究等设置，有利于学生在知识建构过程，体会数学的共通性及关联性.其原因除了来源于知识内容的相似性，也是本着利于学生知识建模的方向完成.

数学是知识点关联性非常强的科目，知识之间既有横向的平推，又有纵向的深入，因而数学的学习过程实际上是一个三维知识系统的建立.对于学生来说，三维知识系统的建立就如同建构一座知识大厦，每层知识是什么内容，上下知识如何联结，这些都是决定了知识系统是否合理坚固的重要因素.所以，“模块融合”在有效建立知识链的同时，还有效挖掘知识点之间的关联，把链变成网，从而有利于学生自主建构知识系统.

数学家华罗庚曾说过“能把书从薄变厚，又能把书从厚变薄”，我们进行模块内融合就是希望学生能学会多角度多层次看问题，发现知识之间的联系，将知识像树木生长一样，由主干延伸构建合理完善的数学知识体系，从而更有利于知识的抽取和综合应用.

(二)“模块融合”促进学生良好的“数学素养”

在新课程标准中，数学素养被提到一个相当的高度，学生的数学素养不仅表现在能解题上，更体现在其数学理解和应用能力.在数学教学过程中应重视培养学生多方面的能力，注意学生的情感态度的发展.“模块融合”紧扣新课程有标准的指导思想，从这一思路出发，寻求“模块间融合”的课程设置，以培养学生良好的“数学能力”.

在上文的课堂呈现中，我们能清楚感受到“模块融合”教学促进了学生“数学素养”的形成.环节1 改变了以往课堂的问题解决方法，而是由学生提出问题，其可行性来源于前面几节课的融合课程的铺垫，学生对于用函数解决方案问题有了一定的认识和体会，其感性认识已提升到一定的高度.所以学生可以成功的提出问题，其“推理能力”已然展现，而教师需要做的只是将学生提出的各个问题进行归纳和总结，变成三个有层次有递近的关键问题.环节2 中，与传统的班级教学比较，从函数的角度理解这一不等式的应用问题，部分学生已能比较顺利的得到实际花费与购物原价之间的关系，能比较深刻的理解两个变量之间的变化联系.在构造函数的过程中，发现变量的分段性质，从而顺利实现分类，突破了原教材中“分类思想”的思维起点和障碍.之后用函数的方式在每一分类中，进行两个函数的比较，特别是从图象角度理解，充分展示了学生“数形结合”思想的内化.而环节3 可以说是学生数学素养的一个亮点体现，不同于之前学生的先分类再构造函数的方法顺序.学生根据“实际花费随着购物原价的变化而变化”这一特征，分析得到这两变量之间存在一定的关系，即函数.从而直接得到“分段函数”，再利用两分段函数的图象进行非常形象的比较.学生的符号意识、分析能力、推理能力都在这一过程中得以体现.当然虽然只是少数学生的思维能力激发，但也从一定程度上反映了“模块融合”教学促进了学生数学素养的形成.

“模块融合”从“利于学生数学能力形成”这一思路入手，进行模块间融合，将不同模块的内容串通起来，实现其数学本质的联结.同时打破现有的模块划分，将不同模块内容放在一起，虽然需要学生更高的学习能力，但可以达到更好的学习效果，从而同时培养了更多核心概念，进而提升了学生的综合运用水平.使得数学模块之间不再是割裂的个体，而融合成为统一的数学整体.正如上文所述，学生通过函数与不等式的融合学习，潜移默化中培养了数感、符号意识和推理能力，所以才能在解决上述问题的过程中，不断尝试不断探究，形成课堂上的发散与创新.当然以上尝试对于学生理解和接受能力提出了更高的要求，学生一旦接受并领悟之后，将非常有利于其数学能力的形成，也将使学生在未来的数学学习过程中终身受益.