立足教材，拓展知识*——例谈初中数学对教材知识点的拓展

广东省中山市黄圃镇中学(528429) 王斌

知识点是构成学习内容的相对独立的最小单元，根据学生所需要的技能和大纲的要求，可将知识点学习的程度分成不同的水平：有的需要认识;有的需要理解、掌握、应用.在教材中，也常以选学内容出现，如新人教版八年级上册《十字相乘法》和九年级上册《21.2.4 一元二次方程的根与系数的关系》.本文以人教版教材为例，选取部分教材内容，从知识点的角度拓展教学内容.

一、什么是拓展教材?

拓展教材，应该从内容的广度和深度来理解.

(一) 内容的广度[1]

内容的广度是指知识点的多少.拓展教材内容的广度体现为增加的知识点的多少，对所拓展的内容的知识点进行提取，教材中没有的知识点即为拓展的知识点.

(二) 内容的深度[1]

内容的深度是指数学知识的抽象程度.人教版数学教材的编排设计是循序渐进，螺旋上升的，如在七年级下册学平方根，八年级下册学二次根式，学习的内容由易到难.从学生地认知水平和能力来看，这样的安排有其合理之处.但在教学实践中，我们发现因为学习的时间间隔了一年，在学习二次根式时，学生已经遗忘了平方根的知识.学生对数学知识的理解是零散的，孤立的，知识的再现和问题解决过程困难重重，容易导致学生缺乏学习信心.

二、何时需要拓展教材?

在与一线教师的访谈中，我们总结得到以下几种情况：

(一) 学生的学情水平

学生的学情水平是影响我们拓展内容广度和深度的重要因素.在教学过程，当我们发现教材内容无法满足学优生的胃口时，就需要我们从深度挖掘教材，拓展学生思维;当学完一章书时，我们需要对全章知识点进行联系总结，这就需要我们根据学情适当增加知识点.

(二) 教材编写未尽详尽之处

受特定形式和篇幅的限制，现行的初中数学教材具有内容呈现的零碎性、数学语言的简洁性和教学导向的隐蔽性等特点，这就需要我们教师对教材进行“再创造”.我们试图通过拓展教材弥补教材编写的缺陷，将相关数学知识看成一个整体展示给学生，注重思维训练，以求学生有完整、全面的认识.

(三) 经典题型以及常用的解题策略

教材由于篇幅的限制，一些经典的题型只能以例题或课后习题的方式出现，稍稍带过.但其中所蕴含的解题技巧、数学思想却不是一道题就可以完全掌握的，学生需要反复锤炼，需要在变式练习找到解题策略.因此需要我们教师立足教材例题，从数学思想、数学方法拓展教材.

(四) 难点突破

有些知识，教材上可能只是一句话，但为了让学生更好的理解，我们必须加以拓展.如人教版的八年级上册《13.3 等腰三角形》中描述等腰三角形“三线合一”的性质时，教材只用了一句话：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.但如何理解，如何应用? 教材涉及到的题目很少.因此，我们要引导学生将这一句话拆成三句话：

已知△ABC中，AB=AC，AD与BC相交于点D，则有以下三个结论：

(1) 如果AD平分∠BAC，则AD⊥BC，BD=CD(由顶角平分线得到底边的中线、高);

(2) 如果AD⊥BC，则AD平分∠BAC，BD=CD(由底边上的高得到顶角平分线、底边上的中线);

(3) 如果BD=CD，则AD平分∠BAC，AD⊥BC(由底边上的中线得到顶角平分线、底边上的高).

然后根据这三句话，给出对应的习题应用性质，巩固知识.

三、如何拓展教材的知识点?

途径一：对章内知识点进行综合应用

案例1 与三角形有关的角

1.1 教材内容

人教版八年级上册《与三角形有关的角》

1.2 聚焦学情

学生已经掌握了三角形的角平分线、三角形的外角和内角.在课后习题中，有如下题目：如图1所示，已知△ABC中，∠ABC、∠ACB的平分线相交于点O，试说明∠BOC与∠A的关系.

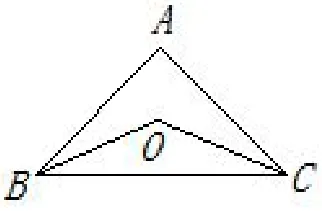
图1

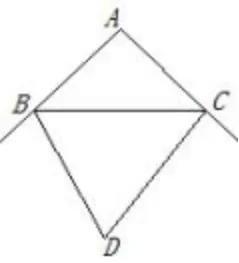
图2

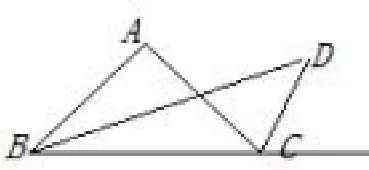
图3

1.3 拓展课程

1.3.1 拓展一：增加外角的角平分线

例1 如图2，已知△ABC中，∠ABC、∠ACB的外角平分线相交于点D，试说明∠D与∠A的关系.

例2 如图3，已知△ABC中，∠ABC的角平分线与∠ACB的外角平分线相交于点D，试说明∠D与∠A的关系.

1.3.2 拓展二：增加找规律的题目

例3 如 图4，∠ACD是△ABC的外角，∠ABC的平分线与∠ACD的平分线交于点A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，A3，···，∠An-1BC的平分线与∠An-1CD的平分线交于点An.设∠A=θ.

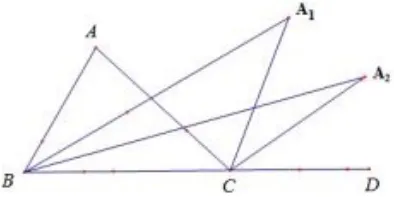
图4

(1) 求∠A1的度数;

(2) 求∠An的度数.

1.4 拓展内容分析

原教材上的课后习题涉及到的知识点有内角的角平分线、三角形的内角和，

拓展一增加的知识点有“三角形的外角等于与它不相邻的两个内角的和”，拓展二在拓展一的基础上增加了类比、归纳的数学思想.

案例2 中点四边形

2.1 教材内容

八年级下册平行四边形

2.2 聚焦学情

依次连接任意一个四边形各边中点所得的四边形叫中点四边形.教材上没有这一节内容，但却是考点之一.学生已经掌握了平行四边形、矩形和菱形的性质和判定方法，会熟练运用中位线定理.因此，中点四边形可视为是对《平行四边形》和《中位线定理》的综合应用.

2.3 课程拓展

探究一基础问题探究

问1 如图5，E、F、G、H分别是四边形ABCD各边上的中点，请你判断中点四边形EFGH的形状，并证明.

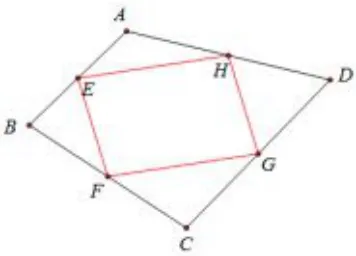
图5

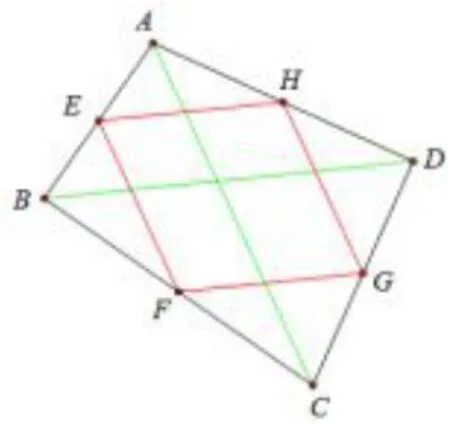
图6

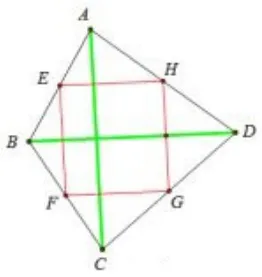
图7

探究二探究影响中点四边形形状的因素

教师让学生动手操作，研究以下两个问题：

问2 如图6，四边形ABCD中，AC=BD.E、F、G、H分别是四边形ABCD各边上的中点，请你判断中点四边形EFGH的形状，并证明.

问3 如图7，四边形ABCD中，AC⊥BD.E、F、G、H分别是四边形ABCD各边上的中点，请你判断中点四边形EFGH的形状，并证明.

师生归纳决定中点四边形EFGH的形状的主要因素是四边形ABCD的对角线的长度和位置.

学生自己动手操作，仔细观察四边形由“一般四边形变成平行四边形(矩形、菱形、正方形)”，猜想并发现中点四边形形状并完成表格.

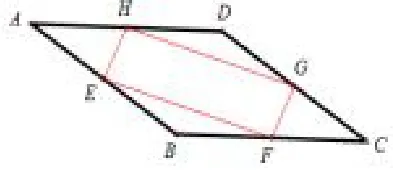
图8

图9

图10

图11

原四边形任意四边形平行四边形矩形菱形正方形中点四边形

2.4 拓展内容分析

教材《平行四边形》所涉及的知识点是平行四边形、矩形、菱形、正方形的性质和判定.中点四边形在此基础上，增加了中位线定理这个知识点.

途径二：选用教材的选学内容

案例3 《21.2.4 一元二次方程的根与系数的关系》

3.1 教材内容

一元二次方程根与系数的关系，即韦达定理.

3.2 聚焦学情

本节课是在学生已经学习了一元二次方程的解法的基础上，对一元二次方程根与系数之间的关系进行的探究.教材的重点在于利用求根公式猜想验证跟与系数的关系，但关于它的应用涉及较少.

3.3 课程拓展：韦达定理的应用

例1 已知2 和-1 是方程2x2+mx+n=0 的两个根，求m和n的值.

例2 已知m,n是二次方程x2+1999x+7=0 的两个根，求(m2+1998m+6)(n2+2000n+8)的值.

例3 已知方程x2-5x+8=0 的两根为x1,x2，求下列代数式的值：

(1)x21+x22; (2)

3.4 拓展内容分析

教材中的选学内容只是韦达定理的内容，即已知方程求两根的和与积.而拓展的三道例题则增加了对韦达定理的应用：例1 是已知两根确定方程;例2 增加了根的定义;例3 增加了完全平方公式、分式的运算.

途径三：高频考点或者是解题的需要.

案例4 《二次函数》

4.1 教材内容

九年级上册《第二十二章二次函数》

4.2 聚焦学情

学生已经学习了二次函数的一般式y=ax2+bx+c和顶点式y=a(x-h)2+k，并能利用配方法将一般式转化为顶点式，研究二次函数y=ax2+bx+c的图象和性质.

4.3 课程拓展

4.3.1 拓展一：图像形状与|a|的关系

利用几何画板绘制一组二次函数图像，如y=3x2+x+1，y=3x2+2x+2，y=-3x2+4x，y=-3x2.学生观察这四个图像的形状，得到结论：当|a|相同时，抛物线的形状相同.

4.3.2 拓展二：如何求出二次函数的对称轴

教材在第38 页，利用配方法得到y=ax2+bx+c的对称轴是x=教师在二次函数的图像上任意选取纵坐标相同的两点(x1,m)和(x2,m)，观察x1,x2的值与对称轴的关系，从而得出对称轴x=

4.3.3 拓展三：二次函数的第三种解析式——交点式

已知二次函数y=ax2+bx+c与x轴交点坐标为(x1,0)和(x2,0)，则根据韦达定理，从而，我们可以得到：

我们把y=a(x-x1)(x-x2) (其中x1,x2为ax2+bx+c=0 的两个实数根)称为交点式.当已知的点为图像与x轴的交点坐标时，我们就可以利用交点式来求函数的一般解析式.

4.4 拓展内容分析

《二次函数》这一章，我们给出了三个拓展.与教材原知识点相比，拓展一增加了二次项系数a与图像形状的关系(原知识点只是研究开口大小与a的关系);拓展二增加了图像上的点的横坐标与对称轴的关系;拓展三增加了第三种解析式：交点式.