一道椭圆离心率问题的多解及推广*

四川省内江师范学院数学与信息科学学院(641100)蒋红珠 李 玉 刘成龙

问题(2016年山西四校联考(二))已知F1、F2是椭圆的左右焦点,P 是椭圆上一点(异于左、右顶点),过点P 作∠F1PF2的角平分线交x 轴于点M,若2|PM|2=|PF1|·|PF2|,则椭圆的离心率为____.

简评该问题具有一定的难度、深度和广度,不偏不怪、解法多样、内涵丰富、数学味浓、不设陷阱、可一般化,有助于学生加深知识理解、发展数学思维、完善认知结构、体验数学研究程式.因此,该试题是一个值得研究的好问题.

为便于下文叙述,先作以下说明：

如图1,F1(-c,0)、F2(c,0)是椭圆=1(a ＞b ＞0)的两个焦点,A1(-a,0)、A2(a,0)为x 轴上的两顶点,B(0,b)为y 轴正半轴上的顶点,e 为椭圆离心率,P 是椭圆上异于A1、A2的一动点,设∠F1F2P=2β,∠PF1F2=2α,∠PMF2=δ,F1P=m,PF2=n,PM=v,F1M=t,F2M =2c-t.

图1

一、问题解决

问题解决常常被看作是能动的、不断发展的过程,是数学思维不断数学化的过程,是一个探索、发现、创新的过程.[1]从不同角度解决问题,有助于学生多角度理解问题,发展求异思维.

分析1特殊化视角

问题作为一个填空题,从小题巧做的思路来看,可以考虑将问题特殊化.

方法1设P 与B 重合,O 与M 重合.因为2|PM|2=|PF1| · |PF2|,可 知2b2=a2,又a2=b2+ c2,得e =

分析2模型化视角

数学模型是将具体的数学关系抽象出来反应特定的问题或特定的事物系统的数学关系或结构,一般以公式或者结论的形式呈现.数学模型代表一类数学问题,是一类数学问题的高度概括与解决.下面从模型的视角来解答.

方法2如图1,由文[2] 构建的模型可知：e =整理得由正弦定理得

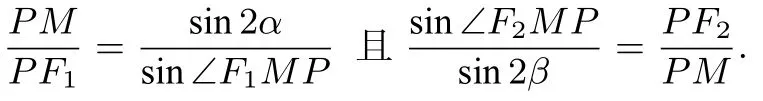
由2|PM|2=|PF1||PF2|,可得

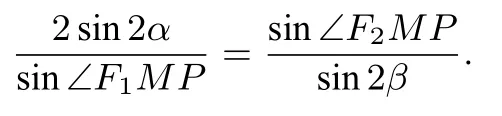
由∠F1MP +∠F2MP =π,∠F1MP =+β-α,得

所以

即2 sin 2α·sin 2β =cos2(α-β),所以

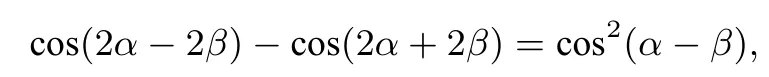
即

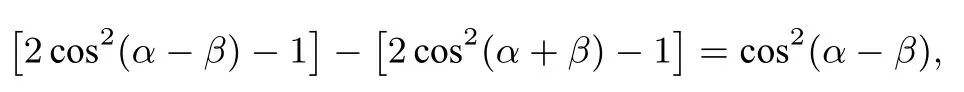
整理得cos2(α-β)=2 cos2(α+β),则

方法3如图1,由角平分线定理得则所以t=me,同理2c-t=ne.由余弦定理可知

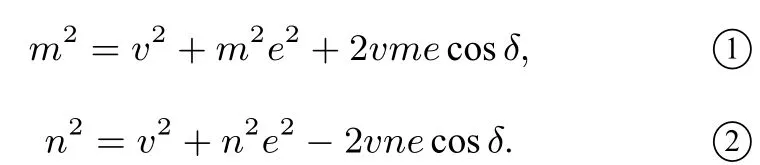
又因为2|PM|2=|PF1| · |PF2|,所以则由①×n+ ②×m,可知

分析3向量视角

方法4由题意得即

解得

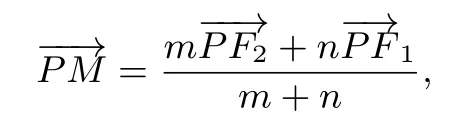
则

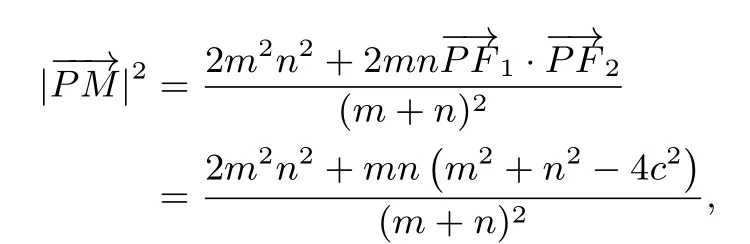
又因为2|PM|2=|PF1|·|PF2|,可知

解得

点评分析1 是最简单的方法,也是最容易想到的办法,分析2-3 有助于学生对椭圆的概念、几何性质、余弦定理的理解,有助于培养学生的运算求解能力、转化与划归能力.

二、问题推广

张景中院士指出：“推广是数学研究中极其重要的手段之一,数学自身的发展在很大程度上依赖于推广.数学家总是在已有知识的基础上,向未知的领域扩展,从实际的概念及问题推广出各式各样的新概念、新问题.”[3]

分析1已知条件2|PM|2=|PF1|·|PF2|中的“2”很特殊,于是尝试将“2”推广成一般量k.

推广1已知F1、F2是椭圆(a ＞b ＞0)的左右焦点,P 是椭圆上异于左、右顶点的一动点,过点P 作∠F1PF2的角平分线交x 轴于点M,若k|PM|2=|PF1|·|PF2|(k ＞1),则椭圆的离心率为

证明提示由方法4,可知

由k|PM|2=|PF1|·|PF2|得又因为m+n=2a,所以所以

分析2问题研究的是“∠F1PF2角平分线”这一条件下的离心率,自然想到将条件改成“△F1PF2边F1F2的中线、高线”,问题的结果会有什么样的变化呢?

推广2(中线)已知F1、F2是椭圆(a ＞b ＞0)的左右焦点,P 是椭圆上异于左、右顶点的一动点,过点P 作△F1PF2边F1F2中线交x 轴于点M,若k|PM|2=|PF1|·|PF2|,且|PF1|·|PF2|=sa2(k,s ＞0),则椭圆的离心率为(其中)

证明提示因为PM 为中线,所以

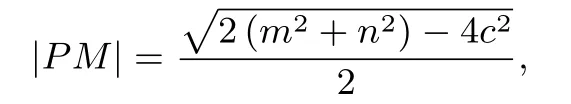
所以由k|PM|2=|PF1|·|PF2|,可知mn,即又因为m+n=2a 且|PF1|·|PF2|=sa2,所以所以离心率为

推广3(高线)已知F1、F2是椭圆(a ＞b ＞0)的左右焦点,P 是椭圆上异于左、右顶点的一动点,过点P 作△F1PF2边F1F2高线交x 轴于点M,若k|PM|2=|PF1| · |PF2|,且|PF1| · |PF2|=sa2(k,s ＞0),则椭圆的离心率为(其中且

证明提示由海伦公式可知

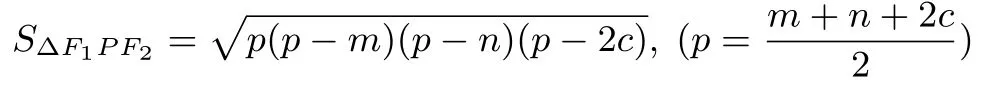
又因为

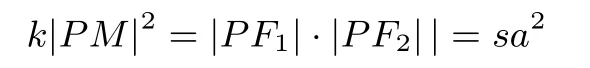
且m+n=2a,则

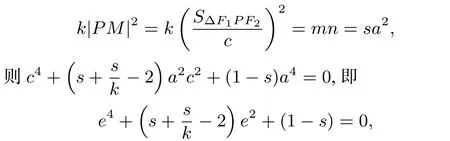
分析3问题以椭圆为载体,背景改为双曲线呢? 继而将新问题的条件改成双曲线中“∠F1PF2的角平分线、△F1PF2边F1F2的中线、高线”,问题的结果又将如何变化呢?

推广4(角平分线)已知F1、F2是双曲线(a,b ＞ 0)的左右焦点,P 是双曲线上异于左、右顶点的一动点,过点P 作∠F1PF2的角平分线交x 轴于点M,若k|PM|2=|PF1| · |PF2| 且|PF1| · |PF2|=sa2(k,s ＞0),则双曲线的离心率为(其中

证明提示由方法4,可知

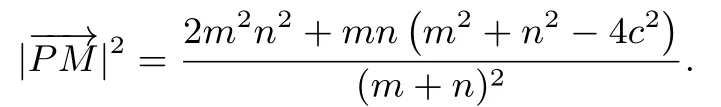
由k|PM|2=|PF1| · |PF2| 得又因为|m - n|=2a 且|PF1| · |PF2|=sa2,所 以所以

推广5(中线)已知F1、F2是双曲线(a,b ＞0)的左右焦点,P 是双曲线上异于左、右顶点的一动点,过点P 作△F1PF2边F1F2中线交x 轴于点M,若k|PM|2=|PF1|·|PF2|,且|PF1|·|PF2|=sa2(k,s ＞0),则双曲线的离心率为其中

证明提示由中线的性质可知

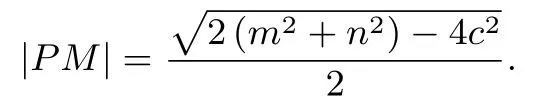
由k|PM|2=|PF1|·|PF2|得又因为|m-n|=2a,|PF1|·|PF2|=sa2,所以所以

推广6(高线)已知F1、F2是双曲线(a,b ＞0)的左右焦点,P 是双曲线上异于左、右顶点的一动点,过点P 作△F1PF2边F1F2高线交x 轴于点M,若k|PM|2=|PF1|·|PF2|,且|PF1|·|PF2|=sa2(k,s ＞0),则双曲线的离心率为其中Δ2=且

证明提示由海伦公式可知

又因为

点评立足成立条件、结构及解决方法将原问题进行推广,对培养学生发现问题、提出问题、分析问题和解决问题有积极意义.