云模式下制造服务评价指标的集成赋权方法*

谢 灿，高新勤，王雪萍，席海洋

(1.西安理工大学 机械与精密仪器工程学院，西安 710048；2.西安交通大学 经济与金融学院，西安 710061)

0 引言

云制造是一种面向服务的制造新模式[1]。在云模式下，制造服务提供方通过制造服务运营方的云制造服务平台，向制造服务需求方提供各类制造服务，从而实现“分散资源集中使用，集中资源分散服务”[2]。

目前，针对云制造服务组合评价与优选问题，常见的方法是通过指标赋权将多目标模型转化为单目标模型进行求解。陈浩等将熵值法和层次分析法(AHP)相结合用于指标赋权，避免了单一评价方法的片面性[3]。陈友玲等采用偏好舵法和变精度粗糙集理论计算评价指标的主客观权重，将综合求得的效率值作为评价依据[4]。Kumar and Singal采用AHP法、理想解相似度排序法(TOPSIS)和改进的TOPSIS方法选择最佳的材料[5]。Sadigha等提出使用模糊AHP-TOPSIS算法对合作伙伴进行评估，从而确定每个任务的获胜企业[6]。通过指标赋权将云制造服务组合多目标优化问题转化为单目标问题可以获得最优解，但指标赋权的主、客观方法很多，如何集成两种主、客观赋权方法并发挥各自优势需要做进一步研究。

本文将G1-法和变精度粗糙集理论分别用于云模式下制造服务评价指标的主、客观赋权，同时引入基于最大熵原理的组合系数模型，集成主、客观赋权结果对云制造服务评价的影响，解决传统综合赋权法因依赖主观而可靠性不高以及未能发挥主、客观两种赋权方法作用的问题。

1 云模式下制造服务的评价指标

1.1 云制造服务配置过程

在云模式下，制造任务的粒度通常较大，需要由多个制造服务提供者共同完成。云制造服务配置就是按照一定的服务要求和逻辑关系，实现制造服务的供需匹配。具体配置过程包括任务分解、可行服务集获取以及服务优选等3个阶段[7]。

(1)任务分解。将粒度较大的云制造任务分解为多个粒度适中且可被单一制造服务提供者完成的子任务。

(2)可行服务集获取。从云制造服务平台中获取满足各个子任务需求的可行服务集。

(3)服务优选。从各个可行服务集中优选云服务，形成组合服务，共同完成大粒度的制造任务。

1.2 云制造服务评价指标

影响云制造服务评价的因素很多，通常采用的评价指标有时间、成本、质量、可靠性、提供商经营状况以及服务评分等。

(1)服务时间T，指云制造服务从被使用到被释放回到云平台所消耗的时间。

(2)服务成本C，指服务需求方获取云制造服务支付的费用。

(3)服务质量Q，指云制造服务能够满足服务需求方的程度，通常由服务需求方参考云平台提供的服务质量评估标准而获得。

(4)服务可靠性R，指云服务在服务需求方限定时间内完成服务次数与服务总次数的比值。

(5)服务提供方经营状况S，指服务提供方的经营能力，通常以其在云平台上单项服务的年营业收入为衡量标准。

(6)服务评分E，指服务需求方对服务提供方相关服务的综合评价，通过历史交易数据获取。

1.3 服务评价指标规范化

由于计量单位和评价准则不同，云制造服务的各指标存在较大差异，需要进行规范化处理[8]。

服务质量Q、可靠性R和评分E为正向指标，越大越好，以服务质量Q为例，归一化公式为：

(1)

服务成本C属于负向指标，越小越好，其归一化公式为：

(2)

服务时间T和服务提供商经营状况S属于区间型指标，以服务时间T为例，其归一化公式为：

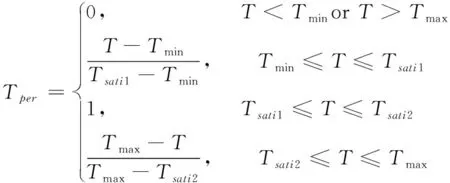
(3)

式中，Tmax和Tmin为可接受的最大、最小交货时间，[Tsati1,Tsati2为服务需求方满意的交货时间区间。

2 云服务评价指标的集成赋权方法

为了兼顾主观偏好和客观真实，本文提出基于最大熵原理的集成赋权方法。首先将G1-法和变精度粗糙集理论分别用于云模式下制造服务评价指标的主、客观赋权。然后采用基于最大熵原理的组合系数模型，集成主、客观赋权结果对云制造服务评价的影响。

2.1 G1-法求取指标权重

G1-法是一种通过主观排序和两两比较赋值反映指标重要程度的赋权方法[9]，主要步骤包括：

(1)确定服务时间、成本、质量、可靠性、经营状况和评分等云制造服务评价指标的主观权重并按降序排列，即a1>a2>…>an。

(2)根据表1给出相邻云制造服务评价指标ak-1与ak相对重要程度之比的理性赋值rk，即：

ωk-1/ωk=rk(k=n,n-1,…,3,2) (4)

(3)计算权重系数ωk，即：

(5)

ωk-1=rkωk(k=n,n-1,…,3,2)

(6)

根据公式(5)可获得云制造服务评价指标a6的权值系数ω6，代入公式(6)反复迭代，可依次获得各云制造服务评价指标的权重系数ω5,ω4,ω3,ω2,ω1。

2.2 变精度粗糙集模型

本文采用抗干扰能力较强的变精度粗糙集模型对云模式下制造服务评价指标进行客观赋权[4]。

云制造服务评价信息决策表为：

I=(U,L=A∪W,V,F)

(7)

式中，U为云制造可行服务有限论域的非空子集，p条历史交易记录记为U={x1,x2,…,xp}；L为云制造服务属性集；A={a1,a2,…,a6}为6个服务评价指标属性集；W={a7}为服务决策属性集；V为L的值域；F为各个服务属性到值域的映射函数。

设Xg=U/A={X1,X2,…,X|U/A|}为云制造可行服务集U通过6个指标属性集A划分得到的等价类，Yh=U/W={X1,X2,…,X|U/W|}为U通过决策属性集W划分得到的等价类。若存在Xg⊆Yh，则Xg关于Yh的相对错误分类率为：

(8)

式中，|Xg|为等价类Xg中可行制造服务组合的个数。

在β∈[0,0.5)时，Yh关于A的β的下近似为：

(9)

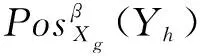
云制造服务指标属性的信息量表示该指标对组合服务集的分类能力，信息量的大小反映了分类能力的强弱。任一服务指标ad的信息量γ(ad)为：

(10)

云制造服务指标属性的被依赖度表示该指标属性被决策属性分类依赖的程度，被依赖度越大则该指标越重要。任一服务指标ad的被依赖度λ(ad)为：

(11)

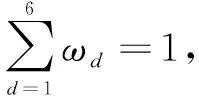
(12)

2.3 主、客观集成赋权

赋权法分为乘法赋权法和加法赋权法。乘法赋权法存在“倍增效应”，这里采用加法赋权法。常见的加法赋权法在分配各方法权重时较为主观，不能发挥多个目标的效用，本文采用基于最大熵原理的集成赋权方法。

云模式下制造服务评价指标的真实权重在数理统计中为一个随机变量，不同的主、客观赋权方法所得的权重则是该随机变量的一个样本值，赋权方法的组合系数则是对应样本的发生概率[10]。在已知制造服务评价指标信息的前提下，概率的合理分布可通过最大化熵求得。广义距离和指云制造服务组合方案的指标参数值与理想值的加权距离和，其值越小代表评价对象整体越接近理想值。因此，基于最大熵原理的赋权方法集成了最大化熵和最小化广义距离和两个方面。

构造基于最大熵原理的集成赋权方法的组合系数模型为：

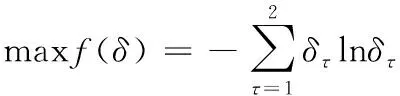
(13)

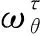
μ1为拉格朗日乘子，构造拉格朗日函数，通过归一化和驻值条件求解全局最优解为：

(14)

对偶规划为：

(15)

3 实例分析

在云模式下，某制造任务可分解为5个粒度适中的子任务，每个子任务可选择的可行服务依次为2、3、6、3、2个。根据式(1)～式(3)，对216种云制造服务组合方案的评价指标T、C、Q、R、S和E进行归一化处理，结果如表2所示。

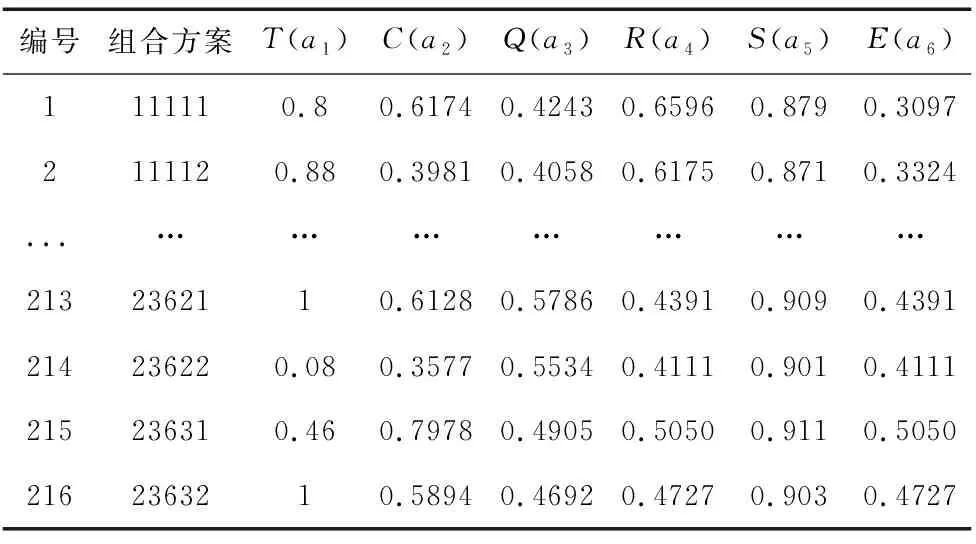
表2 云制造服务组合方案的评价指标参数(部分)

3.1 客观赋权法

从归一化处理后的云制造服务组合方案中随机提取12条历史记录，采用K-means聚类方法对其进行聚类化预处理[11]，并将聚类序号写入参数后的括号中，结果如表3所示。

表3 聚类后的云制造服务组合方案评价指标参数

以原编号203组合方案的服务时间T为例，阐述变精度粗糙集模型中云服务指标属性的信息量和被依赖度的计算过程。“0.84(4)”表示该组合方案的评价指标a1归一化数值为0.84，聚类序号为4。

表3中被选中的决策类Y1=U/d1={x3,x8,x10}，未被选中的决策类Y2=U/d2={x1,x2,x4,x5,x6,x7,x9,x11,x12}。根据评价指标属性a1划分的等价类为X={X1,X2,X3,X4,X5}={{x1,x2,x3,x4,x5,x8,x10,x12},{x6},{x7},{x9},{x11}}，由式(10)可得：

γ(a1)=(82+12+12+12+12)/122=68/144

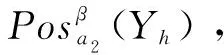
同理可得：λ(a1)=9/12，λ(a3)=7/12，λ(a4)=9/12，λ(a5)=10/12，λ(a6)=8/12。

将云服务指标属性的信息量和被依赖度代入公式(12)可得各指标的客观权重为ωa=[0.25,0.20,0.14,0.12,0.14,0.15]。

3.2 主观赋权法

由G1-法获得6个云制造服务评价指标的主观排序为：

根据表1对相邻服务指标进行理性赋值，即：

r2=ω1/ω1=1.2，r3=ω2/ω3=1.4，r4=ω3/ω4=1.1，r5=ω4/ω5=1.1，r6=ω5/ω6=1.2。

代入公式(5)，得：

将ω6代入公式(6)反复迭代，可依次获得各云制造服务指标的权值系数分别为ω5=0.1271，ω4=0.1397，ω3=0.1538，ω2=0.2153，ω1=0.2582。

因此，6个云制造服务评价指标ak(k=1,2,…,6)的主观赋值保留两位小数后为ωb=[0.26,0.22,0.15,0.10,0.13,0.14]。

3.3 集成赋权法

采用Matlab对基于最大熵原理的集成赋权模型进行仿真，结果如表4和图1所示。广义距离和Cs的上下界3.745和3.731分别对应单一目标最小广义距离和与最大熵，折线区间为两个目标均起作用的有效解。分析可知，随着广义距离和Cs的减小，组合系数的差异增大，评价结果的差异变小。

表4 基于最大熵原理集成赋权方法的组合系数和评价值

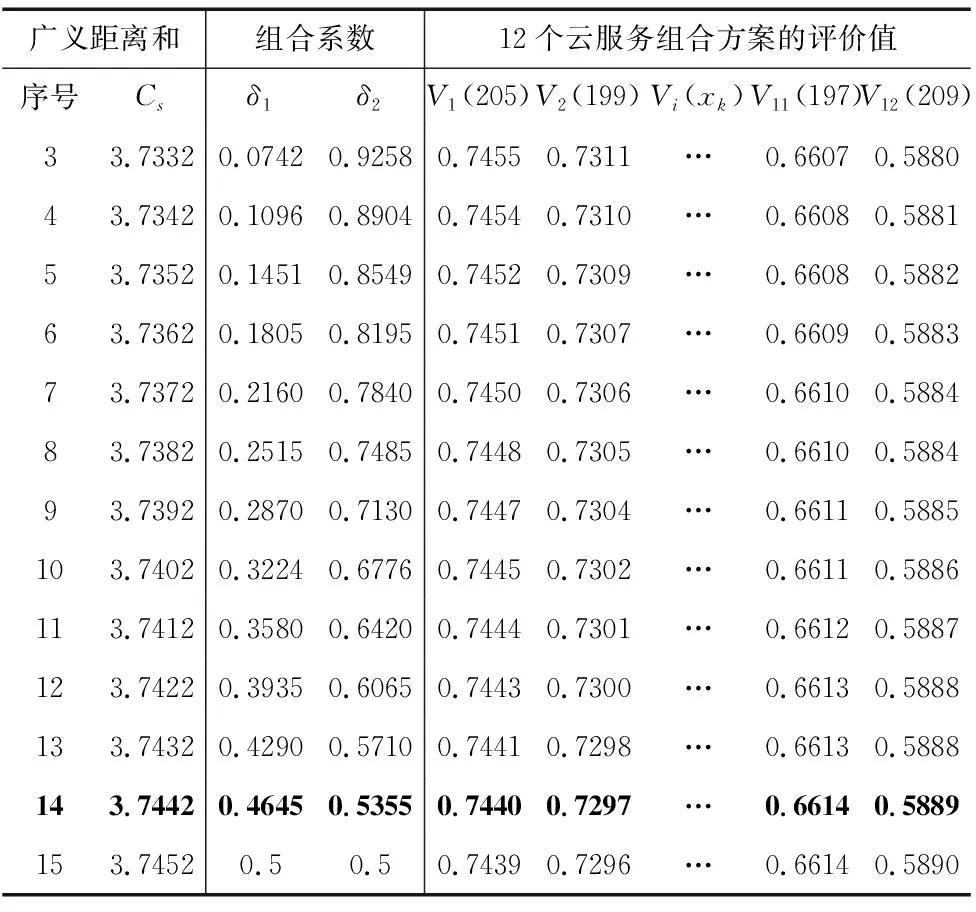
续表

选取广义距离和Cs=3.744进行分析，此时δ1=0.4645，δ2=0.5355。集成主、客观两种赋权方法，云制造服务评价指标的最终权重为ω=δ1ωa+δ2ωb=[0.26,0.21,0.16,0.11,0.13,0.14]，云制造服务组合方案排序结果为205>139>199>213>203>127>195>187>115>198>197>209。

图1 云制造服务组合方案的评价值

将文献[3]的AHP法和熵值法应用于本案例，获得ωa=[0.38,0.23,0.13,0.08,0.09,0.09]，ωb=[0.24,0.03,0.12,0.21,0.33,0.07]，综合赋权为ω=[0.31,0.13,0.12,0.15,0.21,0.08]，用于表4可得排序结果为：

205>139>199>213>115>203>127>195>187>198>197>209。

比较两种方法发现，仅方案115的排序从第9位前移至第5位，其他方案的排序保持不变。选中的方案为205、139和199，因此这种变化不影响云制造服务组合方案最终的选择结果。

将文献[3]的组合赋权用于表2可得排序为205>211>139>199>175>169>19>55>67>47>49>7>33>43>213。将本文集成赋权用于表2可得排序为12>211>205>139>199>175>67>19>33>169>55>47>7>36>213。根据交易记录可知，优于方案199一定可行，弱于方案213则一定不可行，因此两种方法均未将方案213之后的方案列出。分析发现，交易历史所选中的方案位列两种方法全部方案的前五名，符合优选条件；同时，优于方案213的所有方案仅有两个存在不同，两种方法的评价结果差异不大。本文所提方法具有良好的优选性能。

4 总结

首先将G1-法和变精度粗糙集理论两种主、客观赋权法，分别用于云模式下制造服务评价指标赋权；然后采用基于最大熵原理的组合系数模型，集成两种赋权评价结果，协同主、客观赋权法对云制造服务评价的影响。最后通过实例分析和比较研究，验证了基于最大熵原理集成赋权方法的正确性和可行性。本文所提方法解决了传统综合赋权法因依赖主观而可靠性不高以及未能发挥主、客观两种赋权方法作用的问题，具有良好的优选性能。本文所采用聚类方法适用于中小规模数据，后续将对聚类方法进行深入研究，并探讨该方法较启发式算法的优越性。