串一条美丽的项链 让主题复习增值——以《直柱体的体积和侧面积》为例

江苏省常州市金坛区段玉裁实验小学 张 扬

复习课不是旧知识的简单再现和机械重复，而应把它看成是启发学生在原有基础上的一种较高层次的学习过程。有效的复习课，复习内容与形式不能仅仅局限于对旧知识的回顾与串讲，也不该沉迷于试题的机械训练之中，而应通过旧知识的复习，以旧引新，化难为易；以舍求得，化腐为奇；以点带面，化少为多，让学生有新的发现、新的理解和新的体会。数学知识犹如一粒粒散落的珍珠，如果不会整理，只是一盘散沙，没有太大的价值，只有串成美丽的项链，才会价值连城。

一、创设“纵向数学化”思维活动的起点

课始，提出问题：截止到目前，我们小学阶段已经研究过哪些立体图形？（随学生的口答贴出：长方体、正方体、圆柱、圆锥）

收集并展示交流课前整理的作业单：

学生通过自主交流，分享自己的整理以及对体积公式的理解。

随后教师相机提出：外形不一样的长方体、正方体和圆柱都可以用V=Sh，它们之间究竟有什么共同的特征呢？请看——先播放孩子们上交数学补充习题的视频，如果把一本本补充习题想象成一个个平面图形——长方形，随着孩子们不断向上叠加，就会形成立体图形——长方体，再课件演示从长方形（正方形或圆）逐渐向上平移增厚变成长方体（正方体或圆柱）的过程。

拓展直柱体的认知范畴，追问：你发现了什么？

生1：它们上下底一样，中间一样粗细。

生2：长方体是由长方形向上平移形成的，正方体是由正方形向上平移形成的，圆柱是由圆向上平移形成的。

教师相机指出：数学上，通常把这样的立体图形叫作“直柱体”。现在，大家明白这三种立体图形有什么共同特征了。继续追问：除了由长方形、正方形、圆平移形成这三种直柱体之外，你认为直柱体还可以长什么样子？

学生不断围绕直柱体的特征展开想象：由平行四边形、梯形、三角形……平移都可以得到直柱体，随着孩子的想象与口答，课件继续呈现直柱体，再次追问：它们都是直柱体吗？

生：是的，它们都是由平面图形平移得到的立体图形。

建模直柱体体积计算公式，教师提出：那如何求它们的体积？有什么统一的方法呢？

生1：V=Sh，因为它们都是直柱体。

生2：它们都可以变形转化成长方体，因此，都可以用V=Sh。

小结：是呀，只要用上“转化”的策略，就能统一所有直柱体的体积计算公式V=Sh。（相机播放直柱体体积推导的微视频）

二、在序列化交流中深化直柱体体积计算模型

变式练习一：制造这根钢管，要用多少钢材？

图1

图2

反馈时绝大多数学生选择了图2的方法，也有少数的同学选择了图1的方法。

课堂中，通过对比，沟通两种方法之间的联系，学生再次惊奇地发现直柱体体积通用公式的合理性。这样计算比用“大圆柱体积-小圆柱体积”的算法简洁、好算。通过复习，学生感悟到以前看似孤立的各个体积计算公式之间有着密切的联系。从复习旧知识衍生出新知识，从“零碎”的知识之中发现内在的联系，学习由零碎变系统，由厚变薄的过程。

变式练习二：你知道金鱼的体积是多少吗？

（1）把一条金鱼完全浸没在一个底面直径是20厘米，水深12厘米的圆柱形容器中，水没有溢出，且量得水面上升了 2 厘米。这条金鱼的体积是多少立方厘米？

把另一条金鱼也完全浸没在一个长为20厘米，宽为12厘米，高为15厘米的长方体容器中，水没有溢出，且量得水面上升了2厘米。这条金鱼的体积是多少立方厘米？

教学中，通过问题引领：你知道金鱼的体积是多少吗？对比发现无论是用圆柱体的容器，还是长方体的容器，都是通过“等积变形”把金鱼的体积转化为上升水柱（实为圆柱体或长方体形状的直柱体）的体积。在交流对比的过程中，学生深刻理解了直柱体体积公式的本质，虽然底面的形状变了，形成的立体图形的形状也变了，但是直柱体都是平面图形向上平移形成的立体图形，因此直柱体的体积都可以用V=Sh。

引发思考：为什么计算圆锥体积不能用V=Sh？

学生通过几何直观对比，辨析发现了圆锥不是直柱体，从而实现数学思维活动走向深层次的思考。

三、在知识迁移中统一直柱体侧面积计算方法

谈话：我们刚刚研究了直柱体的体积，都是底面积乘高。我们是怎么研究的？（整理发现——引发猜想——推理验证——得到结论）你觉得接下来我们会研究什么？（表面积）

自主交流立体图形的表面积整理单，提出问题：直柱体的体积都可以用V=Sh，那直柱体的表面积里又有什么变与不变的呢？你有什么发现？

学生面露难色，教师相机引导：瞧！这是我们经常遇到的练习，有什么相同之处？

（1）一个长方体饼干盒，长19厘米、宽11厘米、高20厘米。如果在它的侧面贴一圈包装纸，包装纸的面积至少有多少平方厘米？

（2）一个圆柱体饼干盒，底面半径10厘米，高20厘米。如果在它的侧面贴一圈包装纸，包装纸的面积至少有多少平方厘米？

学生通过交流发现（1）要求的是长方体四周的面积（少数孩子提出其实就是求长方体的侧面积），（2）要求的是圆柱的侧面积。列式对比，通过乘法分配律转化发现——长方体四周的面积也可以用底面周长×高来计算。

回顾整理，动眼观察，沟通联系：S直柱体的侧面积=Ch。

引导：我们在整理的时候发现侧面展开图将曲面转化为平面图形——长方形，从而找到了长方体、正方体、圆柱这些特殊的直柱体侧面积计算的方法都是底面周长乘高，那其他的直柱体的侧面积呢？这只是我们的猜想（打上问号），还需要验证，你打算怎样验证？先想一想，再与你的同桌交流。（大多数孩子想到了沿直柱体的高剪开，都可以将直柱体的侧面化曲为直，长方形的长就是直柱体的底面周长，长方形的宽就是直柱体的高，从而进行验证）

随着孩子们的动脑思考、动口说理，教师提出要求：平面图形通过向上平移得到立体图形，就像这一张张纸不断叠加，就得到一个长方体，其实这张纸还可以干嘛呢？

追问：你知道里面还藏着什么吗？想不想知道？我们来动手做一做，出示一张长方形纸。

提出要求：你打算围一个什么样的直柱体？想一想，围一围，说一说。

汇报交流：通过围你发现了什么？

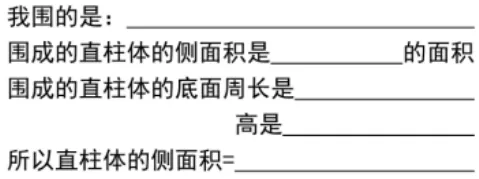
让学生利用手中的A4纸进行移一移、围一围等操作，让他们观察会发生怎样的变化，从而发现数学中的圆柱、长方体、正方体等直柱体体积和侧面积的变与不变，在知识建构的过程中沟通联系，形成知识脉络，经历知识变厚、变薄的全过程。

复习课设计数学化主题活动，从“同一知识领域”内容的关联性出发，发展后续需要的数学核心能力，挖掘知识领域内容的“留白处”，激发后续探究的乐趣，让数学主题活动经验的“根”长得更深。