以圆锥曲线焦点弦为一边的三角形面积的探究

浙江省绍兴鲁迅中学 (312000)

徐 耀

圆锥曲线中的三角形面积问题是圆锥曲线有关最值问题中比较常见的一种题型.它结合了数形结合思想、函数与方程思想、化归与转化思想等多种数学思想方法，有利于综合考查考生的能力，是各地高考试题中出现频率较高的热点问题.在高二学生的作业中，笔者发现了这样一道题：

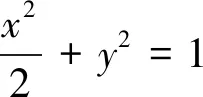
解：设A(x1,y1)，B(x2,y2)，直线l：x=my+1.

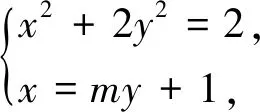
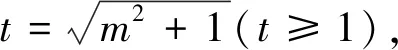
由上题发现，当直线AB的斜率不存在即AB为通径时，ΔAOB的面积最大.

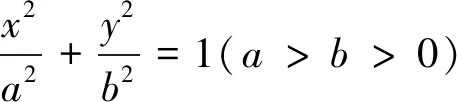
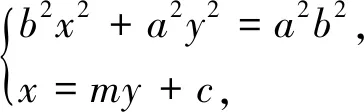
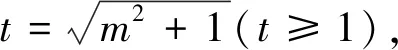
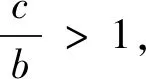
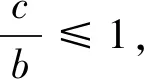
显然当t→+∞时，SΔAOB→0，故无最小值.

综上得以下结论：

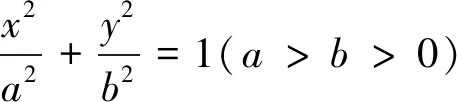
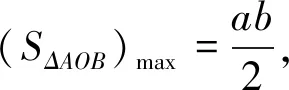
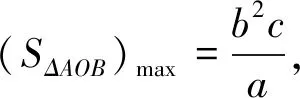
椭圆有这个结论，那么同为圆锥曲线的双曲线和抛物线是否也有类似的结论呢？下面我们先来研究一下双曲线.

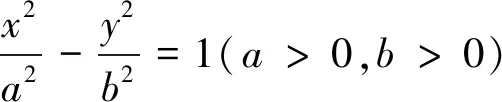
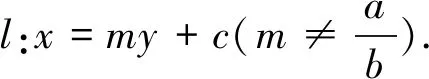
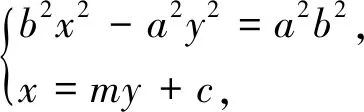
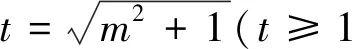
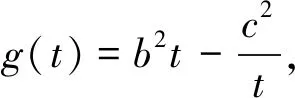
结论2 双曲线中以焦点弦为一边，原点为顶点的三角形面积无最值.

探究三过抛物线y2=2px(p>0)的焦点F作直线l交抛物线于A、B两点，O为原点，求ΔAOB面积的最值.

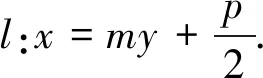
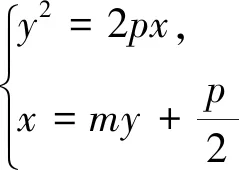
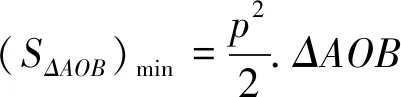
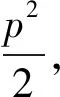
以上结论1和结论3可将原点O推广到x轴上任一点P，从而得到更为一般的结论.由于结论与结论1和结论3类似，读者可试着自己写出.