椭圆中一定点定值问题的推广与拓展*

江苏省海门中学 (226100)

渠怀莲

数学思维新方法的解题表，指出分解和重组是思维的重要过程．分解题目即将题目中的条件的不同部分分开，并研究每一个部分本身，关注更细微的枝节，将题目分解完之后，我们可以尝试将这些元素以一种新的方式重新组合起来，构建一个相关问题或是新问题．G.波利亚在《怎样解题》一书中提出了怎样解题的四个步骤：1.理解题目；2.拟定方案；3.执行方案；4.解后反思．以2017年及2015年江苏复赛试题简答题(三)为例，展现对问题的分解与重组的一般操作手法．

1.试题呈现

(1)直线l是否过定点？若是，求出定点坐标；若不是，说明理由;

(2)过P,Q两点分别作椭圆的切线，两条切线交于点B，求ΔBPQ面积的取值范围．

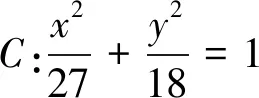
2.试题的通式

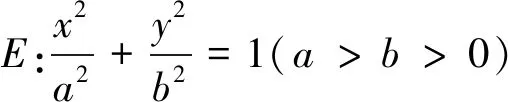
(1)直线l是否经过定点？若是，求出定点坐标；若不是，说明理由；

(2)过点P,Q两点分别作椭圆的切线，两切线交于点M，求ΔMPQ面积的最小值．

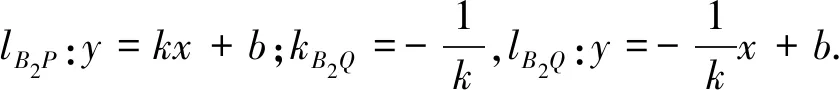
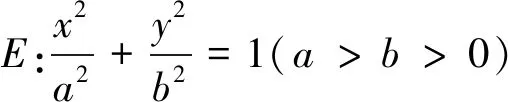
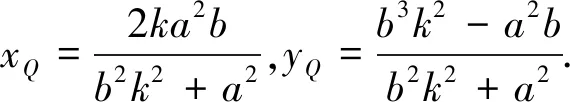
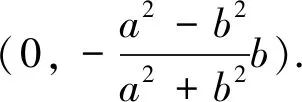
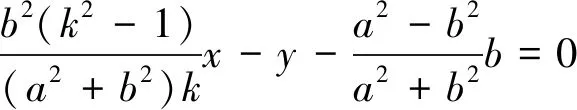
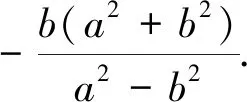
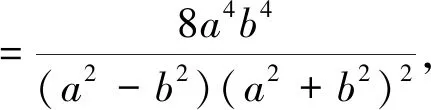
所以ΔMPQ面积的最小值为

3．试题的拓展

拓展1 分解问题的条件与结论，逆命题依然成立.

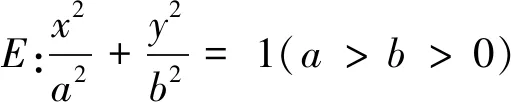
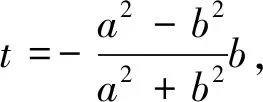
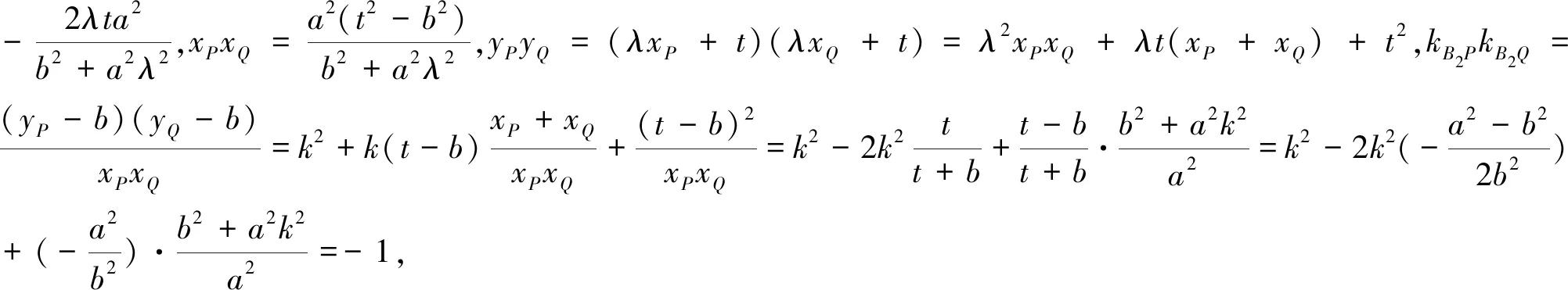
拓展2 条件进一步弱化，重组问题变为开放型试题.

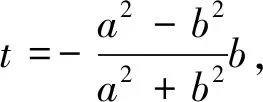
(b2+a2λ2)x2+2λta2x+a2(t2-b2)=0．

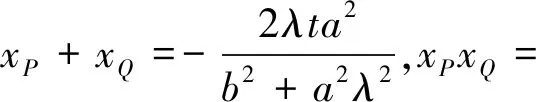
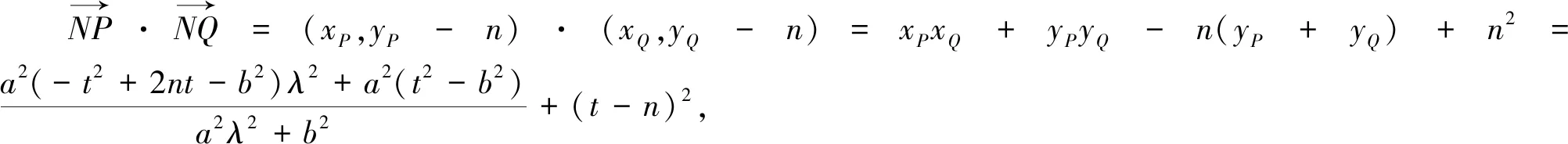
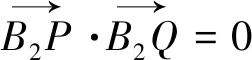
4．结语

根据高中数学竞赛试题的特点，从组织数学探究活动着手，训练和培养数学竞赛解题思维能力．多方位探索解题途径，培养解题思维的灵活性.深入地思考发现数学问题的本质，培养解题思维的深度，辨析和对比转换问题，培养解题的批判性，积淀数学解题策略，切入解决问题的普适性，提升问题拓展引申的能力.