基于演化博弈的行人过街机理与管理对策模型研究
2019-08-03魏科,朱茵,路峰
魏 科, 朱 茵, 路 峰
(中国人民公安大学交通管理学院, 北京 100038)
0 引言
随着城市交通管理理念的发展,步行交通逐渐引起社会各界的广泛关注。日益增长的行人过街需求同保有量与日俱增的机动车在道路时空资源有限的交叉口展开了对路权的争夺。自2012年“中国式过马路”问题被提出至今,各省市相应出台了管理对策,然而行人违法过街行为仍旧存在,2017年仅浙江省一个省全年查处了行人与非机动车闯红灯49.2万起,因此研究“中国式过马路”的内在机理和折射出的管理问题就具有其社会意义。
目前,行人过街研究主要集中在过街现象和过街心理方面的研究。交通流特性研究方面,金生等利用跟车模型进行仿真,结果表明车辆和行人的交互作用降低了车辆的通行能力,增加了车辆和行人的延误[1]。李百兵等考虑了车辆与行人的交互作用,发现交叉口行人的预期等待时间呈U型分布[2]。行人过街心理研究方面,刘荣卿等分析了年龄、时间间隔、时间和车速对行人在交叉口的决策风险[3]。TOVE观察了1 392名行人在道路交叉口的行为,发现男性行人比女性行人过街闯红灯的多,利用回归预测,在不考虑性别因素时,大规模群体的行人比零星数量的行人更倾向于闯红灯[4]。交通设施心理研究方面,LIPOVAC等通过研究行人过街倒计时显示牌,发现无论交通流如何,倒计时显示在统计上大大减少了违法过街行人的总数[5]。
现有对行人过街的研究着重于对现象的静态刻画与重现,而行人违法过街问题实质是在既有道路时空资源和管理政策下各参与方不断博弈的结果。李平将经典的博弈论引入过街行人冲突模型中,构建了人与机动车之间的博弈模型[6]。然而,行人在处理复杂的交通信息时具有局限性,这与经典博弈论中完全理性的假设前提略有不符,而基于有限理性假设的演化博弈能避免这一不足。引入交通行为效用经济学理念来建立模型,刻画行人违法过街行为的内在机理,预测各博弈方的稳定均衡策略,分析管理中存在的问题,提出应对措施,可为管理部门提供管理决策依据。
1 过街行人群体内的动态演化博弈模型
1.1 模型建立
基于过街行人的有限理性和信息的不对称性,对有信号灯控制的交叉口内的过街行人群体的各项参数设定如下:
(1)根据行人到达交叉口后,做出过街决策先后顺序的不同,将过街人群分为X、Y两个群体。
(2)交叉口的行人群体X有两种策略,违法过街或者守法等候;交叉口的行人群体Y在跟随X或者不跟随X这两种策略中选择。
(3)违法过街的行人群体,获得额外的时间收益为r,面临管理部门的经济处罚为M,人身安全风险为S(如:与其它道路使用者发生冲突时造成人身伤亡或者财产损失);守法等候的行人群体,不会获得额外的时间收益,也不会面临经济处罚和安全风险。
(4)行人违法过街时,对行人群体X、Y不同策略组合的处罚力度不同。当只有一个群体违法时,处罚力度为a;当两个群体都违法时,对违法发起者的处罚力度为b,对违法跟随者的处罚力度为c。
(5)由于警力有限,行人违法过街不一定会受到处罚。当行人群体X、Y均选择违法时,两个群体受罚的概率均为p;当只有一方选择违法过街时,受罚概率为q。
(6)对于行人群体X、Y不同的策略组合,各群体所面临的风险程度不同。一方违法,无人跟随时,违法群体面临的风险度为α;一方违法,另一方跟随时,违法发起者和违法跟随者的风险度分别为β,γ。
(7)行人群体X违法的概率为m,行人群体Y跟随的概率为n。
(8)其中a,b,c,p,q,α,β,γ,m,n∈(0,1),r,M,S>0。
根据以上参数,可得过街行人博弈得益矩阵(见表1)。

表1 行人博弈得益矩阵
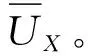
UX(Break)=n(r-Mbp-Sβ)+
(1-n)(r-Maq-Sα)=nR2+(1-n)R1
(1)
UX(Keep)=n·0+(1-n)·0=0
(2)
(3)
则,行人群体X的复制动态方程为:

(4)
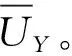
UY(Follow)=m(r-Mcp-Sγ)+(1-m)·0=mR3
(5)
UY(Not-Follow)=
m·0+(1-m)·(r-Maq-Sα)=(1-m)R1
(6)
(7)
则,行人群体Y的复制动态方程为:
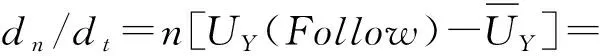
(8)
1.2 模型分析
根据求得的群体X、Y的复制动态方程,通过判断等式右边函数的正负性来分析群体X、Y的策略演变。
令:τ=nR2+(1-n)R1=n(R2-R1)+R1;ε=mR3-(1-m)R1=m(R3+R1)-R1。则求得ε、τ的正负性,便可得知复制动态方程的稳定性和收敛性。
令:θ=R1/(R1-R2) ,φ=R1/(R1+R3)。当ε>0或τ>0时,记为“+”;当ε<0或τ<0时,记为“-”。由于Ri(i=1,2,3)可正可负,则R1、R2、R3的正负情况有8种组合,从而可分8种情形讨论ε、τ的正负性(见表2)。
根据以上计算,可得到4类复制动态相位图(见图1),并求得m、n不同取值所对应的dn/dt(行人Y)和dm/dt(行人X)的复制动态相位图归纳表(见表3)。
将上述两个群体的复制动态在平面直角坐标系中表现出来,可得到过街行人群体X、Y的复制动态关系和稳定性(见图2)。
(1)对比(R1,R2,R3)=(+,+,+)和(R1,R2,R3)=(-,-,-)
当(R1,R2,R3)=(+,+,+)时(见图2a),(m,n)*=(1,1)是行人群体内部博弈的演化均衡策略(ESS),即行人群体Y会选择跟随X违法过街。其原因可能是行人面临的安全风险太低,或者经济处罚力度不够,使得违法过街的收益大于所支付的风险和罚款。
当(R1,R2,R3)=(-,-,-)时(见图2b),(m,n)*=(0,1)是博弈的稳定均衡点。这种情况表示,当行人面临高风险或者高额处罚,使得违法过街所获得的额外收益小于所支付的成本,行人群体X趋于选择守法,行人群体Y跟随X守法。
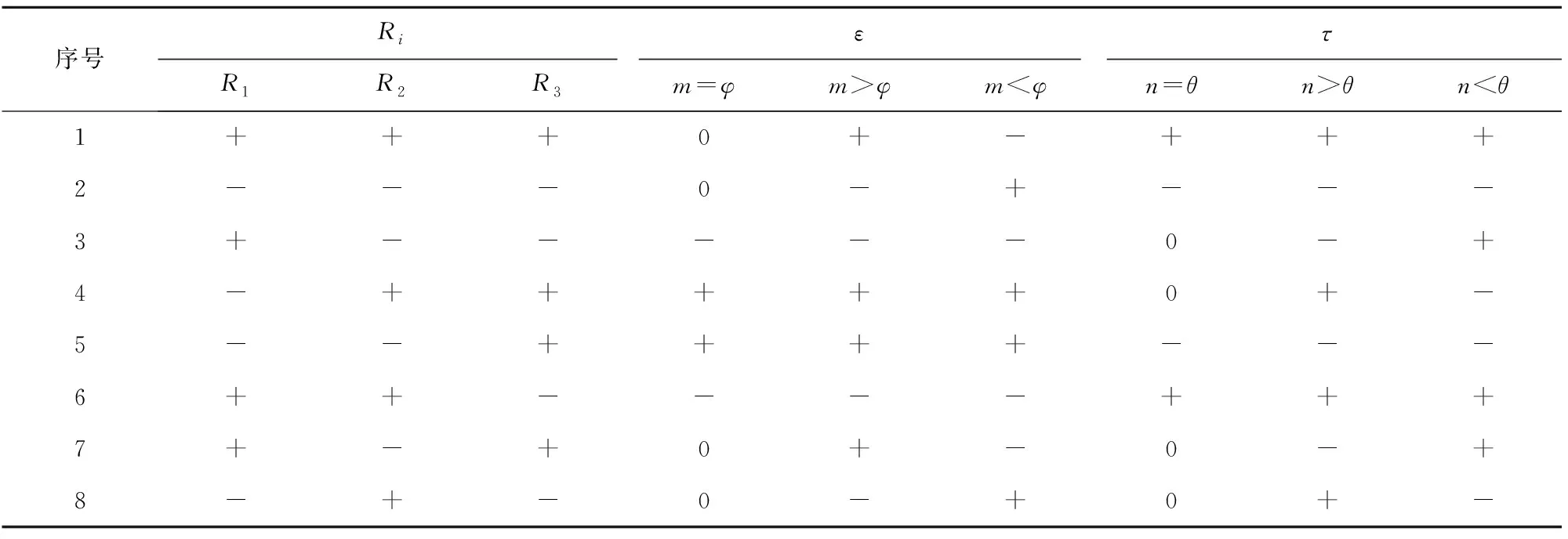
表2 ε、τ正负性判别

图1 复制动态相位图

序号Ri(n,dn/dt)(m,dm/dt)R1R2R3m>φm<φn>θn<θ1+++1(b)1(a)1(d)1(d)2---1(a)1(b)1(c)1(c)3+--1(a)1(a)1(c)1(d)4-++1(b)1(b)1(d)1(c)5--+1(b)1(b)1(c)1(c)6++-1(a)1(a)1(d)1(d)7+-+1(b)1(a)1(c)1(d)8-+-1(a)1(b)1(d)1(c)
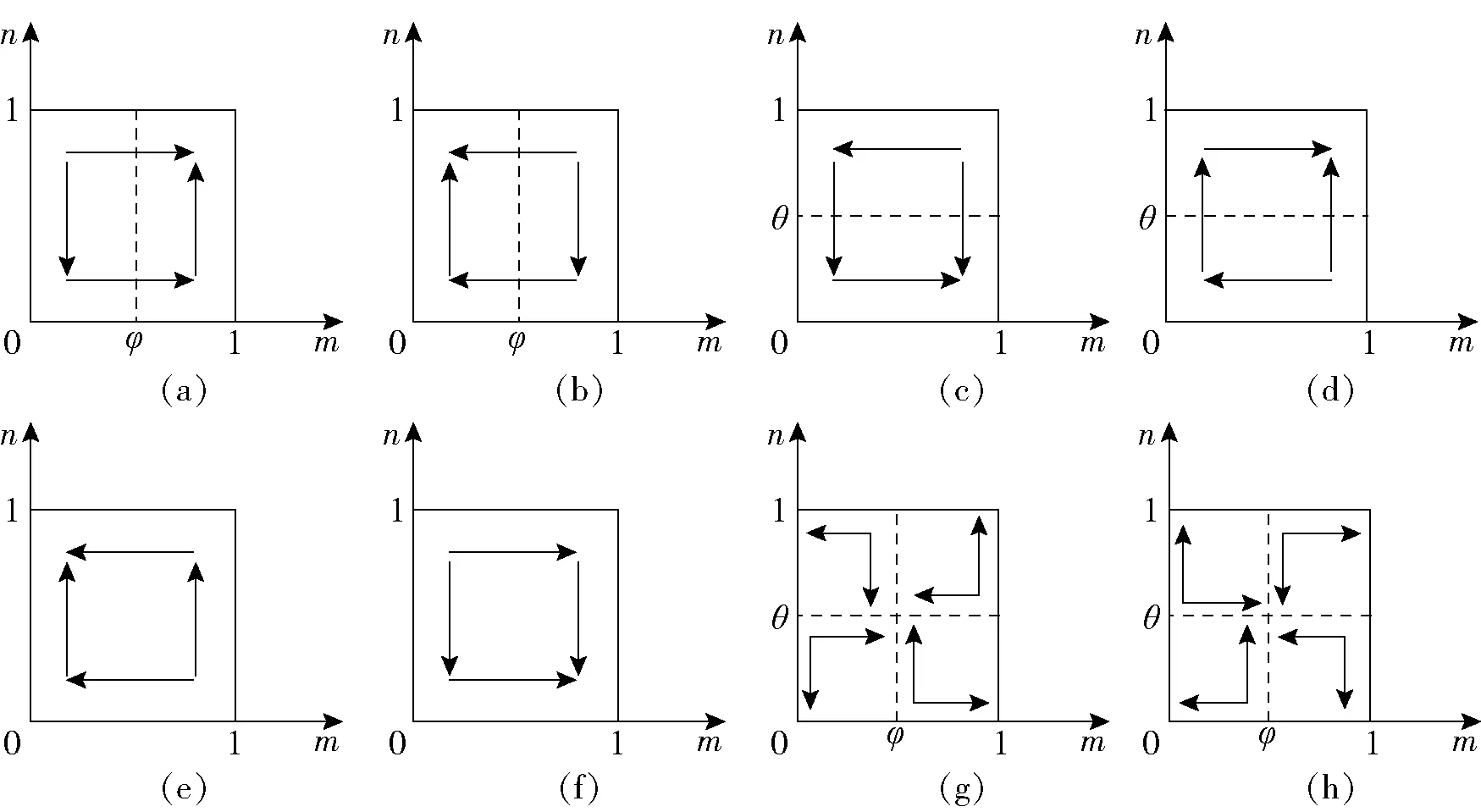
图2 行人群体内部的复制动态关系
(2)对比(R1,R2,R3)=(+,-,-)和(R1,R2,R3)=(-,+,+)
当(R1,R2,R3)=(+,-,-)时(见图2c),ESS是(1,0),即行人群体X倾向于违法,而行人群体Y选择不跟随。造成这种局面的深层原因是,管理部门对有人跟随的群体性违法行为处以高额罚款,而对无人跟随的单个违法情形予以轻微的处罚或者不处罚。
当(R1,R2,R3)=(-,+,+)时(见图2d),博弈的ESS是(1,1)。最终的稳定策略是行人群体Y跟随行人群体X违法。究其原因,可能是 “凑够一波人”过街时,吸引了司机的注意,从而降低了安全风险,或者是对跟随违法的大规模群体采取低的惩罚力度,而对无人跟随的违法群体采取高的惩处力度。
(3)对比(R1,R2,R3)=(-,-,+)和(R1,R2,R3)=(+,+,-)
当(R1,R2,R3)=(-,-,+)时(见图2e),(m,n)*=(0,1)是ESS。这种情况形成的内在机理暗含着对违法发起者采取高额罚款,而对违法跟随者采取轻微罚款或者不处罚的措施,最终过街人群趋于守法。
当(R1,R2,R3)=(+,+,-)时(见图2f),(m,n)*=(1,0)是该情形下的ESS,即行人群体X选择违法,而行人群体Y选择不跟随。造成这种局面的原因是对违法跟随者采取高额处罚,而对发起者轻微处罚或不处罚,这种情况的形成前提一般只存在于理论当中。
(4)对比(R1,R2,R3)=(+,-,+)和(R1,R2,R3)=(-,+,-)
当(R1,R2,R3)=(+,-,+)时(见图2g),演化稳定策略与(m,n)的初始比例有关:
①m>φ,n>θ时,(m,n)*=(0,1)
②m>φ,n<θ时,(m,n)*=(1,1)
③m<φ,n>θ时,(m,n)*=(0,0)
④m<φ,n<θ时,(m,n)*=(1,0)
这种情形的发生,与前提条件有关,即(R1,R2,R3)=(+,-,+),这个前提暗含着管理部门对有人跟随的违法过街行为发起人采取高的处罚力度,而对跟随者采取低的惩治力度;对无人跟随的违法过街行为采取低的惩治力度。
当(R1,R2,R3)=(-,+,-)时(见图2h),演化稳定策略与(m,n)的初始比例有关:
①m>φ,n>θ时,(m,n)*=(1,0)
②m>φ,n<θ时,(m,n)*=(0,0)
③m<φ,n>θ时,(m,n)*=(1,1)
④m<φ,n<θ时,(m,n)*=(0,1)
(R1,R2,R3)=(-,+,-)的情况,意味着在有人跟随违法过街的行为发生时,对跟随者处以高罚款,对违法发起者轻度处理;在无人跟随的违法过街行为发生时,对违法过街发起者从重处罚。在这种措施下,出现了演化稳定策略由行人群体X、Y的比例决定的情形。
不论在何种前提条件下,过街人群X、Y的比例在博弈中不断变化,最终趋于稳定,证明了羊群效应的存在。站在管理者的角度,期望行人都遵守法律,其所追求的ESS是(m,n)*=(0,1),即X最终的博弈决策是守法,而Y选择跟随。
在行人过街的内部博弈中,有四种情形符合管理者的要求,分别是情形2:(R1,R2,R3)=(-,-,-)、情形5:(R1,R2,R3)=(-,-,+)、情形7:(R1,R2,R3)=(+,-,+)时,m>φ,n>θ和情形8:(R1,R2,R3)=(-,+,-)时,m<φ,n<θ。
其中,情形2和情形5的均衡点与(m,n)的初始比例无关。对于情形2,在实际管理中,只要行人违法过街,可对其从重处罚,在不断的演化博弈中,就能达到使行人都守法等候的目的;对于情形5,结合实际,只对违法发起者从重处罚,也能达到使过街行人守法的目的。
对于情形7和情形8,虽然其也能实现(m,n)*=(0,1),但这个均衡点的实现是有前提的,与(m,n)的初始比例有关,在实际管理中,很难估算人群X守法和人群Y跟随的概率,因此形成理想均衡点的前提管理措施只有当(m,n)的初始比例在满足上述条件下才会有效。
2 过街行人与管理部门的演化博弈模型
2.1 模型建立
从行人过街内部的演化博弈可以看出,处罚措施和行人面临的安全风险,影响着行人的过街决策。在实际管理工作中,警力有限,难以对各个交叉口全天候,全覆盖管理;在无人管理的交叉口,行人违法过街的可能性更大。基于此,对将要建立的模型设定如下参数:
(1)行人违法面临的风险程度为F,F是α、β、γ的函数;面临的处罚力度为A,A是a、b、c的函数。
(2)管理部门的管理成本为C,尽职奖励为D,失职处罚为N,行人违法所造成的社会损失L假设由管理部门承担。
(3)在行人守法的情况下进行管理,认为是浪费资源,此时管理部门不获得尽职奖励。
(4)行人P违法的概率为w,管理部门管理T的概率为k。
(5)w,k,A,F∈(0,1),C,D,N,L>0。
根据以上参数,可得行人与交管的博弈得益矩阵(见表4)。

表4 行人与管理部门博弈得益矩阵
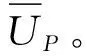
UP(Break)=k(r-MA-SF)+(1-k)(r-SF)=
r-SF-kMA
(9)
UP(Keep)=k·0+(1-n)·k=0
(10)
(11)
则,过街行人的复制动态方程为:
dw/dt=w(1-w)[UP(Break)-UP(Keep)]=
w(1-w)[r-SF-kMA]
(12)
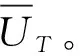
UT(Manage)=w(D-C-L)+(1-w)(-C)=
-C+w(D-L)
(13)
UT(Indulge)=w(-N-L)+(1-w)·0=
w(-N-L)
(14)
(15)
则,管理部门的复制动态方程为:
dk/dt=k(1-k)[UT(Manage)-UT(Indulge)]=
k(1-k)[-C+w(D+N)]
(16)
2.2 模型分析
为了判断行人P和管理部门T的博弈演化趋势,需要先讨论r-SF-kMA和-C+w(D+N)的正负性。令:ρ=(r-SF)/MA,δ=C/(D+N)。记:σ=r-MA-SF,μ=-C+w(D+N);R4=r-SF-MA,R5=-C+w(D+N),v=r-SF。下面将分6种情形讨论σ与μ的正负性(见表5)。

表5 σ、μ正负性判别
同理,可以得到k、w在不同取值下,所对应的dw/dt(行人)和dk/dt(管理部门)的复制动态相位图,并在平面直角坐标系中表现出两个群体的复制动态关系(见图3)。
(1)r-MA-SF>0
当C>D+N时(见图3a),(w,k)*=(1,0)是行人与管理部门博弈的ESS。此均衡点表示,行人会趋向于违法,而管理部门不管理。这与现下状况比较吻合,管理部门的管理成本太高,无法对所有的违法过街行为进行管理,而不管理时,行人所面临的经济处罚为零,以致行人违法过街的总收益大于零,最终选择违法。
当C (2)r-SF-MA<0,且0 当C>D+N时(见图3c),(1,0)是ESS,即行人选择违法,管理部门不管理。这种情况的出现与管理成本和管理措施有关,虽然制定了严厉的惩罚措施,但是由于管理成本较高,这些措施难以得到全方位、全时段、全区域的贯彻执行,使得行人的收益逐渐演变成r-SF-MA>0,最终行人选择违法。 当C ①w>δ,k>p时,(w,k)*=(0,1) ②w>δ,k ③w<δ,k>p时,(w,k)*=(0,0) ④w<δ,k (3)r-SF-MA<0,且r-SF<0 无论是C>D+N(见图3e);还是C 图3 行人与管理部门的复制动态关系 管理部门寻求的最优解是(w,k)*=(0,0),即过街行人都在路口守法等候,符合这种稳定策略的是情况5:r-SF<0且C>D+N、情况6:r-SF<0且C 次优解是(w,k)*=(0,1)和(w,k)*=(1,1),前者对应情况4:0 最糟糕的解是(w,k)*=(1,0),即行人违法,交管不管。出现这种局面的有:情况1:r-SF-MA>0且C>D+N、情况3:0 综上,在大众还未养成守法过街的习惯之前,管理部门在面对行人违法过街行为时,应对违法行为进行约束和管理;否则一旦有人违法过街,行人群体间必定引发破窗效应,造成大面积违法行为的发生。 管理部门在实际应用模型时,应结合本地实际,计算出模型中各参数取值,以确定本地适用于6种管理模型中的哪种情形。例如,当地对各参数的实际估值为r-SF=8,MA=10,C=9,D+N=12,即满足0 图4 (w,k)的复制动态关系图 图5 过街人群违法概率趋势图 图6 管理部门管理概率趋势图 本文分析了灯控交叉口行人过街行为特征,将行人划分为先后做出过街决策的两类人群,基于演化博弈分析了两类人群的策略得益并建立过街行人群体内部的演化博弈模型,得出了行人在全排列组合决策下收益、风险、惩罚下的演化稳定策略,探究了行人过街行为的内在形成机理。结合实际,考虑到管理部门的管理成本,构建了行人与管理部门的博弈模型,揭示了行人与管理部门的收益冲突关系。管理部门在对行人违法过街行为进行管理时,应采取“疏”与“堵”并举的对策:其一,保障行人的路权,合理优化对行人过街的绿灯时间分配,保障行人在交叉口时间资源分配的公平;其二,在确保道路时间资源分配公平的基础上,再对违法过街行为进行处罚,同时加强宣传教育。两种策略并举可从根源上使得博弈平衡逐渐趋于行人守法,且保障了公平。
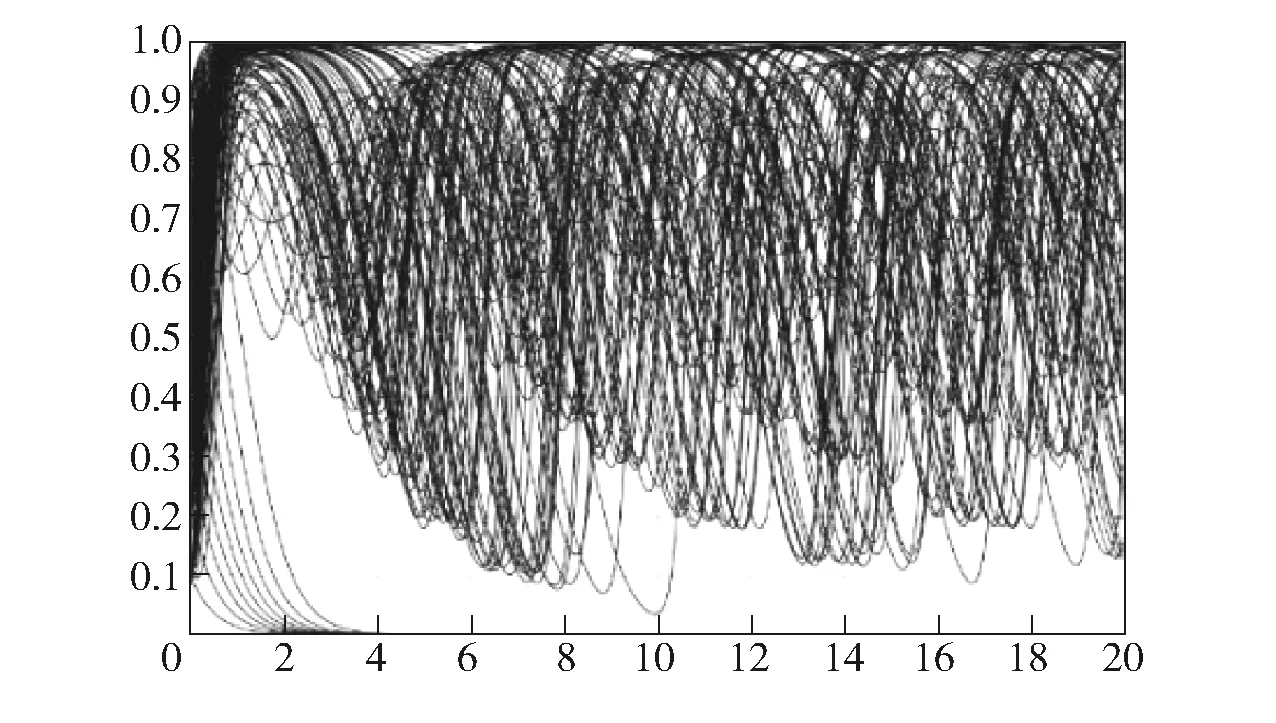
3 模拟计算与分析

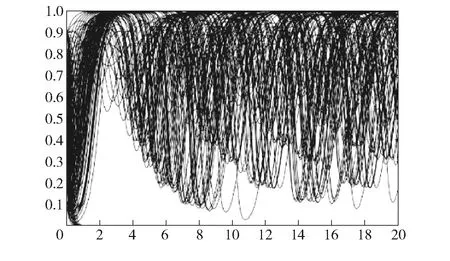
4 结语
