螺栓与孔间隙对紧螺栓连接板孔周应力的影响*
2019-08-02
(南昌航空大学航空制造工程学院 江西南昌 330063)
螺栓连接是一种广泛应用于工程结构的重要连接方式。由于结构件装配的需要,经常在被连接件上加工圆孔以便安装。圆孔的存在使得被连接件材料不仅存在不连续性,而且在承受外力时,容易发生应力集中,使得孔周位置萌生裂纹,从而导致结构产生损伤,降低连接的可靠性。因此,研究螺栓连接孔周应力水平及其与设计参数的关系,是螺栓连接可靠性设计和研究的重要方面,受到国内外研究者的关注。
对于普通螺栓连接而言,影响螺栓连接板孔周应力水平的因素很多,诸如预紧力大小、结合面间的摩擦因数、螺栓与孔的对中性、外部横向载荷以及螺栓孔径的大小等。针对这一问题,国内外学者开展了不少相关研究。为了探讨横向加载下螺栓连接孔周向应力分布,OSKOUEI等[1]建立了螺栓连接板三维有限元模型,分析了预紧力对孔周应力分布的影响,发现增大预紧力能有效地降低螺栓连接孔周应力水平。考虑到连接板几何尺寸对螺栓连接板孔周应力水平的影响,WANG和SHEU[2]分析了12组复合材料构成的螺栓连接板的应力试验结果,计算了连接板孔周应力集中位置的应力强度因子。基于有限元方法,IMURA等[3-4]分析了电机安装螺栓在偏心力和离心力作用下螺栓连接板孔周应力分布。ZHU等[5]研究了静态加载下,标准、较长和较厚3种接头杆的端部螺栓连接孔和上部填充区域内的应力分布规律,发现较厚的接头杆会在螺栓连接孔处产生较高的应力。顾秉栋等[6]讨论了孔距和板厚对螺栓连接孔应力集中系数的影响。徐建新和姜云鹏等[7-8]建立了多排、双剪式螺栓连接板与单排、单剪式螺栓连接板的有限元分析模型,探讨了表面粗糙度对螺栓连接板孔周接触应力的影响。借助实验方法和有限元手段,KEIKHOSRAVY等[9]探讨了连接板尺寸和宽径比对螺栓连接板孔周和孔深方向应力分布的影响。严贤怀等[10]提出了一种估算螺栓连接孔周向应力的方法,以解决利用应变片测量螺栓孔周应力十分困难的问题,并修正了考虑预紧力后的孔周应力分析方法。结合虚拟界面层法,曹勇等人[11]采用填充孔的形式分析了复合材料板螺栓连接接头的应力集中问题,研究发现合理的预紧力能改善螺栓连接孔周应力状态,但无法改善螺栓连接孔边缘附近的层间剪切应力集中状态。采用胶接、螺栓连接和胶接-螺栓连接混合连接3种接头形式,李成等人[12]研究了复合材料板的应力分布,发现采用混合连接可利用低模量胶材料缓解螺栓连接的应力集中,实现比传统连接更好的连接性能。对于不同预紧力作用下的复合材料层合板螺栓单板搭接和双板搭接结构孔,张永杰和孙秦[13]发现增加预紧力可降低层合板孔边拉应力水平,但双板搭接的孔边应力明显低于单板搭接的孔边应力。针对钢结构设计规范中螺栓组设计对螺栓最小容许距离的规定问题,徐忠根等[14]研究了不同螺栓距下螺栓连接头的应力集中,发现增大螺栓距可提高试件的强度。
虽然研究者对螺栓连接板孔周应力分布规律做了很多的研究,但是仍然还有很多规律性问题没有了解清楚。因为机械或人为加工误差、使用过程中的材料磨损、腐蚀环境下的材料受损、热环境下材料受热应力作用导致的材料变形等因素,都会导致螺栓连接件中螺栓孔的形状、尺寸和表面粗糙度等参数受到影响,使得螺栓连接孔直径的实际值和设计值存在一定的误差,而且这种误差是随机的、不可控的。考虑到螺栓孔的存在会使得连接材料发生不连续性变化,是典型的应力集中部位,而且螺栓孔径的变化使得连接板、被连接板的承力截面面积发生明显变化,影响到螺栓孔的应力分布,对螺栓连接板的强度产生影响,本文作者以单搭接单螺栓连接板为研究对象,基于弹性力学理论建立螺栓连接孔周应力影响因素模型,探讨影响螺栓连接板孔周应力水平的各种因素,再通过有限元建模的手段建立螺栓连接板的参数化分析模型,探讨螺栓与孔间隙变化对连接板孔周应力水平的影响。研究结果可为螺栓连接板孔径的优化设计提供支撑。
1 螺栓连接板孔周应力分析
1.1 带孔螺栓连接板应力平衡方程
研究对象为图1所示的单搭接单螺栓连接板,由两块薄板(薄板1和2)和螺栓、螺母组成。假定螺栓为一普通螺栓,薄板1的一端固定,薄板2的一端承受横向外部载荷。

图1 单搭接单螺栓连接板几何模型
以板1为分析对象,建立如图2所示的坐标系Oxyz。为便于理解,假定螺栓头与薄板1的结合面用Ω1表示,板1与板2的结合面用Ω2表示,各结合面在预紧力F0作用下产生的接触压力为fn(x,y,z), 受横向加载F产生的剪切力为τn(x,y,z), 接触面间的摩擦因数用μ表示。
在螺栓对中安装的情况下,Ω1区域的接触压力用fn(x,y,0)表示,剪切力用τn(x,y,0)表示。根据力学平衡条件得到
(1)
(2)

图2 带孔板1的应力分析模型
在螺栓对中安装的条件下,Ω2区域的接触压力用fn(x,y,h)表示,剪切力用τn(x,y,h)表示。根据力学平衡条件得到
(3)
(4)
为保证连接的可靠性,结合面之间产生的最大摩擦力要大于外部横向载荷,即
μF0≥F
(5)
假定用σx、σy、σz、τxy、τyz、τzx分别表示螺栓连接板的各向应力。在不考虑螺栓连接板各结合面间接触应力和剪切应力的条件下,忽略z方向应力的作用,带孔螺栓连接板的应力平衡方程为
(6)
(7)
考虑接触应力和剪切应力的影响,带孔螺栓连接板的应力平衡方程应进行修正。
在Ω1区域,应力平衡方程应修正为
(8)
(9)
在Ω2区域,应力平衡方程应修正为
(10)
(11)
1.2 孔周应力水平影响因素讨论
分析带孔螺栓连接板应力分析模型发现,区域Ω1和Ω2的应力受接触压力和剪切力的影响,而接触压力和剪切力与预紧力、摩擦因数、结合面的面积密切相关,所以孔周应力水平受预紧力、结合面之间摩擦因数以及结合面面积的控制。
因为Ω1区域为一圆环,圆环的外圈直径为螺栓头的直径D1,内圈直径为螺栓孔的直径D,即区域Ω1的表面积由螺栓头和螺栓孔直径决定。Ω2区域的外圈为2e×W的长方形区域,内圈是直径为螺栓孔直径D的圆,即区域Ω2的面积与板几何尺寸e和W、螺栓孔直径D的大小密切相关。
因为区域Ω1、Ω2面积直接影响接触压力和剪切力的分布,而且区域Ω1、Ω2面积随着孔直径D的增大而减小,即接触力和剪切力取值也随着D的变化而改变,所以螺栓连接孔周应力与连接板螺栓孔直径D的值相关。为了探讨螺栓孔径变化对孔周应力水平的影响,求解应力平衡方程即可讨论孔周应力与螺栓孔径的关系。但是,要通过解析方法计算出应力与螺栓连接孔直径的关系相对比较困难,文中结合有限元法侧重分析螺栓孔径变化对连接板孔周应力水平的影响。
2 变孔径螺栓连接板的参数化建模
2.1 螺栓连接板的几何模型
以图1所示螺栓连接件为研究对象,假定板1和板2均为铝合金板。螺栓连接板的几何尺寸如表1所示。铝合金材料的密度ρ=2 740 kg/m3,弹性模量E=71.7 GPa,泊松比ν=0.33。螺栓和螺母材料选用钢,钢材的密度ρ=7 850 kg/m3,弹性模量E=210 GPa,泊松比ν=0.27。

表1 螺栓连接板几何尺寸
2.2 连接板孔周应力坐标
建立如图3所示的孔坐标系(D,α,z)。假定载荷方向为平面极坐标系极轴正方向,逆时针方向为转角正方向,沿螺栓轴线向螺母方向为z轴正方向。

图3 螺栓孔坐标模型
应力计算时,螺栓的直径d保持不变,α的步长取6° 。为了探究孔深不同位置的应力规律,z轴方向取值为z=0、1.5、3 mm。基于以上坐标,可以探析相同深度位置不同螺栓孔直径下螺栓孔边缘应力分布情况,进而了解螺栓与孔间隙对圆孔周向应力的影响程度。
2.3 参数化有限元建模方法
基于Abaqus软件,将图1所示的单搭接单螺栓连接板模型离散化,所有单元均为六面体单元,连接板网格模型如图4(a)所示。考虑到板螺栓孔位置材料的不连续性,孔周属于应力集中区域,所以对孔周位置网格进行了加密,如图4(b)所示。根据几何模型边界,对板1的左端实现完全约束条件。因为文中着重研究螺栓孔周应力分布规律,建模时螺栓和螺母之间采用Tie连接,以提高计算效率。为防止板1和2之间发生相对滑动,建模时对螺栓施加1 000 N的预紧力。板1和2、螺栓头与板1、螺母与板2的接触面均定义为摩擦接触/硬接触,罚系数定义为0.15。计算时,在板2的自由边界施加均布载荷σ1=0.1 MPa。
利用Python语言编程对Abaqus软件包实施二次开发,通过Python直接与Abaqus内核交互,编写接口命令不断调用模型对象,建立螺栓杆与螺栓孔间隙自动变化的计算模型。自动建模时,对每次计算结果数据库对象模型选择性提取数据,提高分析效率。图5所示为带孔螺栓连接板的孔周应力分析流程图。

图4 螺栓连接板的有限元网格模型

图5 孔周应力分析流程图
3 螺栓与孔间隙对孔周应力的影响
3.1 参考设计间隙下孔周应力分布
由于连接板孔周承受拉应力、压应力和剪应力的联合作用,使得孔周应力分布对连接板的可靠性具有不可忽视的作用。由于螺栓孔周区域是轴对称圆柱面,适合采用柱坐标系来描述,文中采用图3所示的柱坐标(α,z)来描述。孔周的Mises应力σr(α,z)可表示为
(12)
其中
σ1=σx(α,z),σ2=σy(α,z),σ3=σz(α,z)
因为孔周容易发生应力集中,结合有限元插值计算的特性,孔周必须进行网格细化,以保证计算结果的准确性。考虑孔周应力最能反映结构的强度特性,文中计算了在结合面不发生宏观滑移时圆孔直径为螺栓杆直径1.1倍时的孔周Von Mises应力云图,如图6所示。结果表明,螺栓孔的附近有应力集中的现象存在,应力集中主要分布在α=0°、90°、180°和270°位置。其中,螺栓头与板结合面、螺母与板结合面处的孔周应力较孔周其他位置的应力明显更大。

图6 螺栓连接板孔周Von Mises应力云图
3.2 螺栓与孔间隙对孔周应力水平的影响
以图3所示的螺栓孔坐标(α,z)来描述孔周各点的位置,提取孔周应力σr(α,z)。 如图7所示,随着孔位置深度z的增加,孔周应力水平不断下降;当z为[0~1.5] mm时,孔周应力水平随孔位置深度z的增加而线性下降;当z为[1.5~3.0] mm时,孔周应力水平与孔位置深度的关系不大。
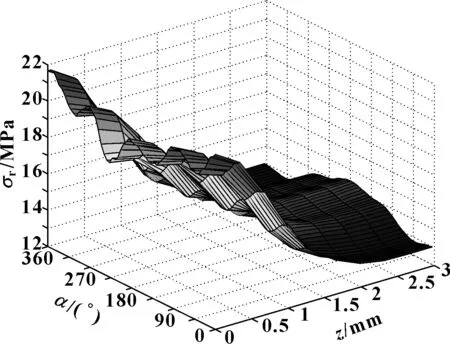
图7 螺栓连接板孔周应力分布
图8描述了孔深z=0位置的螺栓孔周应力分布规律。结果表明:孔边缘应力集中位置不随孔径增大而发生明显变化;随着孔径的增大,螺栓孔周应力水平均发生下降,并且螺栓孔径-螺栓孔边缘应力呈现近似线性负增长关系;当直径比D/d增加25%,孔边缘应力平均下降约45%,负增长比值约-1.8。
图9描述了z=1.5 mm处螺栓孔周应力分布。结果表明:孔周应力集中位置及螺栓孔径-螺栓孔边缘应力水平与z=0处相似;当D/d增加25%,z=1.5 mm处螺栓孔边缘应力水平下降约30%,负增长比值约-1.2。

图8 z=0位置孔周应力水平
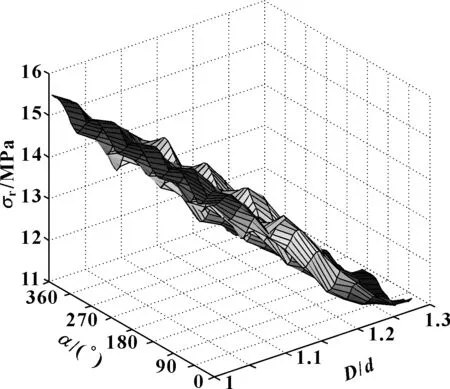
图9 z=1.5 mm位置孔周应力水平
图10描述了z=3 mm处螺栓孔周应力分布。结果表明:孔周应力集中位置分布于α=0° 、90° 、180° 和270° 处,且不随孔径的增大而发生改变,其中α=180° 处应力水平最高;螺栓孔径与孔周应力水平关系呈开口向上的抛物型。当D/d为1~1.1时,螺栓孔周应力水平随孔径的增大而减小;当D/d为1.1~1.2时,孔径的增大对孔周应力水平几乎无影响;当D/d为1.2~1.3时,螺栓孔边缘应力水平随螺栓孔径的增大而增大。
计算结果表明,螺栓与孔间隙对孔周应力水平的影响规律与孔周位置的深度有关,最大应力水平位置在螺栓头与薄板结合面的孔周位置,且应力水平随孔周间隙的增大而减小;最小应力水平发生在两薄板结合面的孔周位置,且当孔径比为1.1~1.2时应力值达到最小。

图10 z=3 mm位置孔周应力水平
4 结论
(1)分析参考设计孔间隙下孔周应力的分布,发现孔周应力水平随孔深度的增加而降低。
(2)螺栓孔径变化对孔周应力集中位置基本上不产生影响,应力集中区域主要分布在α=0°、90°、180°和270°。
(3)增大螺栓孔径,在z=0和1.5 mm 位置孔周应力水平下降,孔径大小与孔周应力水平呈现近似线性负增长关系;当D/d增加25%,z=0处孔周应力水平下降约45%,D/d增加25%,z=1.5 mm处孔周应力水平下降约30%。
(4)在z=3.0 mm处,D/d为1~1.1时,孔周应力水平随孔径的增大而减小;D/d为1.1~1.2时,增大孔径对孔周应力影响甚微;D/d为1.2~1.3时,孔周应力水平随孔径的增大而增大。
