刚玉砂轮外圆磨削微观热流体动压效应分析*

(青岛理工大学机械与汽车工程学院 山东青岛 266033)

对于砂轮磨削而言，不同磨料砂轮的性能各异。陶瓷刚玉磨料性能优异，用途广泛，而且在价格上远低于CBN和金刚石磨料，同时对于磨床及修整装置的要求也不苛刻。陶瓷刚玉磨具适用于多种磨削方式，它可被做成砂轮、砂布、砂纸、砂带、沙盘等多种磨具[1]，而做成砂轮时适宜磨削多种材料，特别是用于外圆磨削时性能优异。在磨削过程中，通常砂轮的局部区域温度会高达600 ℃，而大多数的热量很难被磨屑带走，这就导致热量在砂轮及工件的表面聚集，因此温度对磨削过程的影响是不可忽略的。乳化液作为磨削液时具有良好的散热性和较好的清洁性，可以带走一部分热量。

目前，很多学者对砂轮磨削过程中的流体动压效应进行了研究[2-5]。葛培琪等[6]分析了平面磨削时的流体动压效应，并利用数值分析方法获得了磨削的压力和膜厚的分布，但其将砂轮简化为光滑的表面，并且忽略了温度的影响。通常在表面粗糙度远小于油膜厚度的条件下，才能够将粗糙表面假设成光滑表面。然而，磨削液的膜厚一般为几微米，与表面微观形貌的粗糙度在同一数量级，此时必须考虑砂轮与工件的表面粗糙度。张阔等人[7]通过钢球与平板接触模型，得出了在混合润滑情况下表面形貌的幅值对润滑的影响。王立梅等[8]研究了表面形貌对砂轮内圆磨削时的流体动压效应的影响，但没有考虑砂轮外圆磨削时的情况。考虑微观表面粗糙度的弹流润滑理论称为微弹流理论[9]。本文作者以陶瓷刚玉砂轮外圆磨削轴承钢为研究对象，通过多重网格法和多重网格积分法，分析热效应和表面粗糙度对磨削区流体动压效应的影响，并与采用金刚石磨料、CBN磨料的结果进行比较。

1 砂轮计算模型

建立陶瓷刚玉砂轮外圆磨削的模型，如图1(a)所示，根据线接触弹流润滑理论，将其等效为无限长线接触模型[10]，如图1(b)所示。

图1 砂轮外圆磨削的几何等效图

中心膜厚的计算采用温诗铸和杨沛然[11]回归出的经验公式:

h0=11.9α0.4(η0U)0.74E′-0.14R0.46W-0.2

式中：α为黏压系数;η0为乳化液的环境黏度;E′为当量弹性模量;W为单位长度上的载荷。

2 润滑基本方程及边界条件

考虑热效应的Reynold方程为

(1)

式中：ρ*和(ρ/η)e是当量参数，与乳化液的黏度和密度有关。

当量参数表达式如下：

式中：x为沿速度方向的坐标(m)；p为油膜压力(Pa)；h为膜厚(m)；ρ为密度(kg/m3)；η为乳化液有效黏度(Pa·s)。

膜厚方程为

(2)

其中，

(3)

式中：Sa(x)和Sb(x)分别是砂轮和工件表面的粗糙度函数；Aa和Ab分别是砂轮和工件表面的粗糙度幅值(μm)；La和Lb分别是砂轮和工件表面的粗糙度波长(μm)。

黏压黏温方程采用ROELANDS等[12]的经验公式:

(4)

式中：S为黏温系数，S=β(T0-138)/(lnη0+9.67)；T为实际温度(K)；T0为环境温度(K)；β为温度系数，β=0.042 K-1。

乳化液的密压密温关系经验公式[13]为

ρ=ρ0[1+(0.6×10-9p)/(1+1.7×10-9p)-0.000 65(T-T0)]

(5)

载荷方程为

(6)

式中：w为单位长度上的载荷(N)。

磨削液的能量方程为

(7)

(8)

热传导方程为

(9)

式中：ca、cb分别为砂轮和工件的比热容(J/(kg·K))；ρa、ρb分别是砂轮和工件的密度(kg/m3)；ka、kb分别是砂轮和工件的导热系数(W/(m·K))。

温度在砂轮和磨削液膜接触界面、工件和磨削液膜接触界面应该是连续的，所以应该满足以下界面热流量连续条件：

(10)

砂轮热传导方程的温度边界条件：

(11)

工件热传导方程的温度边界条件：

(12)

3 方程的量纲一化及求解

将基本方程进行量纲一化，并定义如下的量纲一化参数：

采用多重网格法求解压力，所用网格为6层，最底层稀疏网格有31个节点，最高层稠密网格有961个节点。利用多重网格积分法和逐列扫描法分别求解弹性变形和温度T。

4 结果及分析

表1所示为刚玉砂轮、轴承钢和乳化液的基本参数。

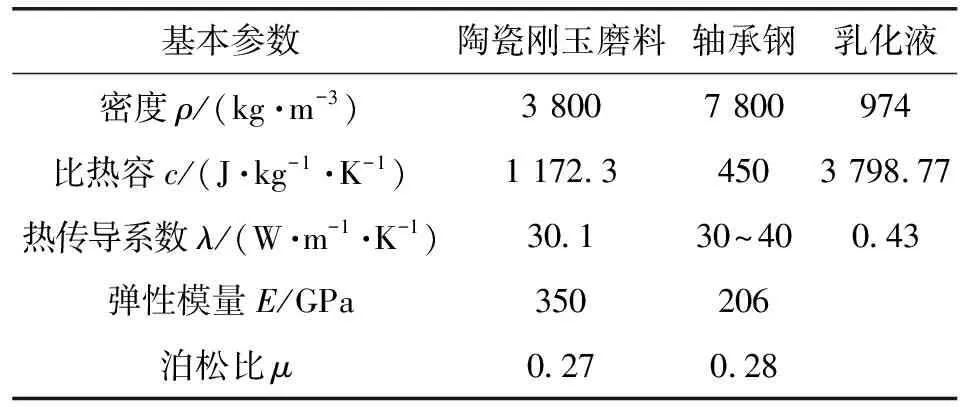
表1 砂轮、轴承钢和乳化液的基本参数

文中计算使用的参数为：砂轮转速35 m/s，工件转速100 r/min，砂轮半径400 mm，工件半径120 mm，采用水包油型乳化液。根据严升明和房风浩[14]的计算方法，求得乳化液的各个参数：η0=1.59×10-3Pa·s，c=3 798.77 J/(kg·K)，ρ=974 kg/m3，λ=0.43 W/(m·K)。取量纲一载荷W=2×10-6。

4.1 不同磨料砂轮压力和膜厚对比

图2示出了考虑热效应时刚玉磨料砂轮与金刚石、CBN(立方氮化硼)磨料砂轮磨削轴承钢(GCr15)的压力和膜厚分布。

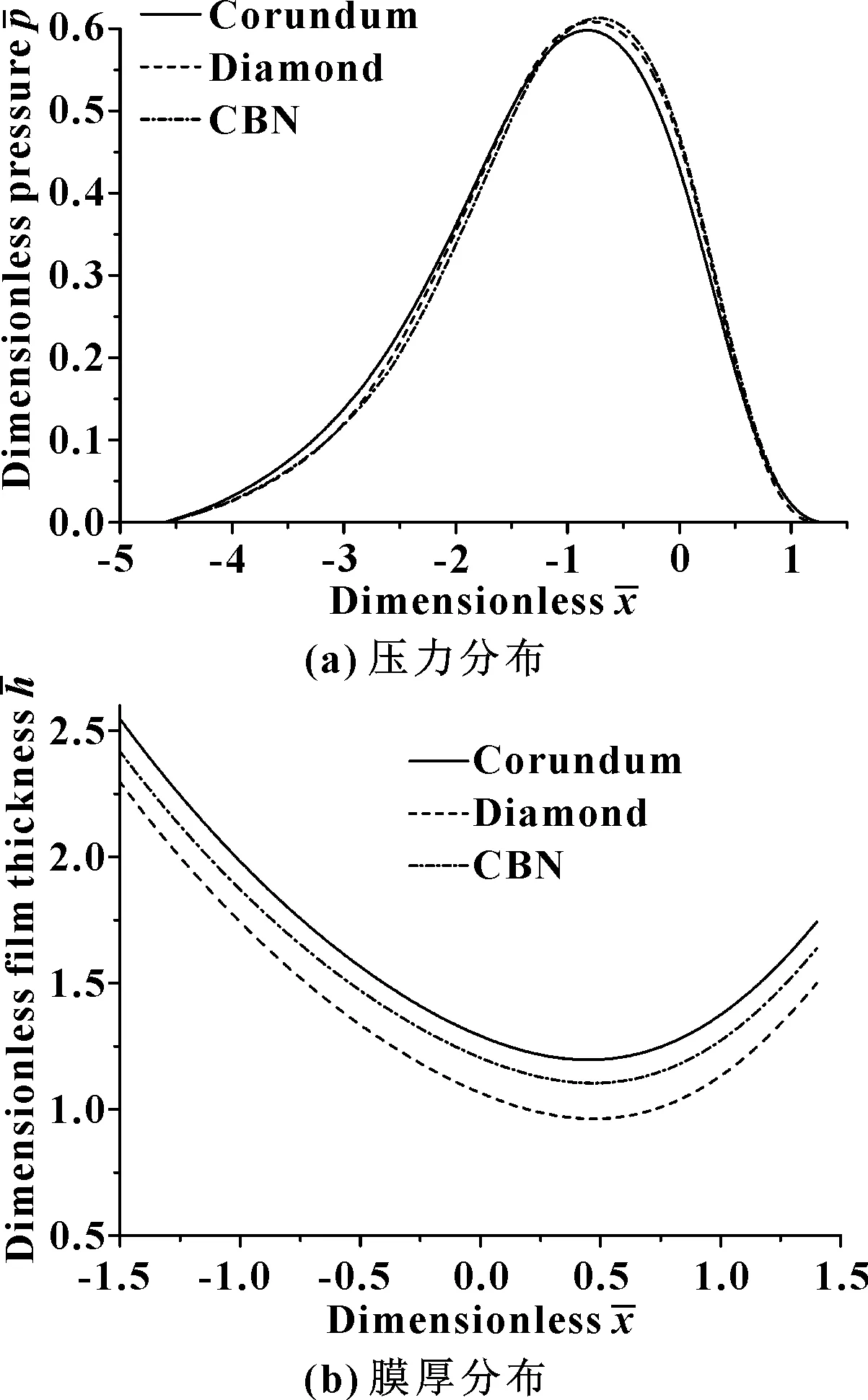
图2 不同磨料砂轮对流体动压效应的影响

可以看出：刚玉砂轮磨削过程时的整体压力最小，最大压力也最小，整体膜厚和最小膜厚最大。从工程实际来讲，磨削时较大的膜厚能够降低磨削时的温升，减少非工作磨粒的磨损。

4.2 热效应对磨削液压力和膜厚的影响

4.2.1 理想光滑表面下热效应的影响

图3示出了未考虑粗糙度的影响时，有无考虑热效应对磨削区流体动压力和膜厚分布的影响。可以看出：温度对磨削区的压力和膜厚的影响比较明显；考虑热效应的影响，相比于等温时压力在入口区增大，在出口区减小，整体压力减小，并且磨削区的压力峰值向左移动；热效应对膜厚的影响表现在平均膜厚变小，最小膜厚相较于等温情况降低约20%。可见，热效应对磨削区流体动压效应的影响是不可忽略的，同时磨削的过程中势必会产生磨削热，所以研究磨削过程时应该考虑温度的影响。

图3 温度对光滑表面流体动压效应的影响

4.2.2 粗糙表面下热效应的影响

图4示出了有无考虑热效应时，表面形貌对磨削区流体动压力和膜厚分布的影响。可以看出：同时考虑热效应与粗糙度对磨削区的压力和膜厚的影响比较大，但整体趋势与理想光滑表面下的热效应的影响相同。

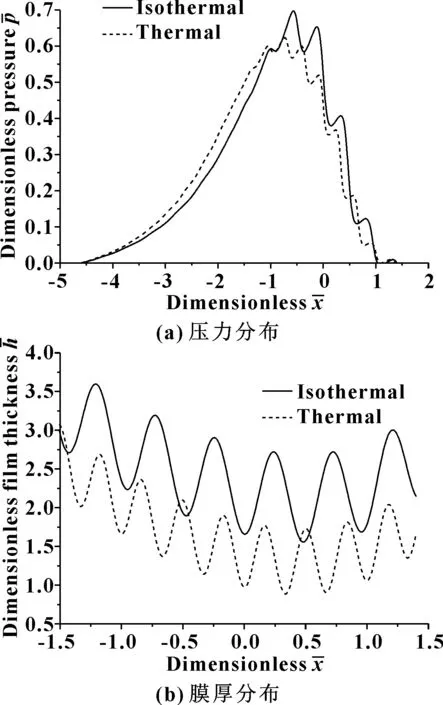
图4 温度对粗糙表面流体动压效应的影响

4.3 考虑热效应时粗糙度对压力和膜厚的影响

4.3.1 粗糙度对压力和膜厚的影响

图5示出了考虑热效应的工况下，表面粗糙度时对砂轮和工件间磨削区流体动压力和膜厚分布的影响。

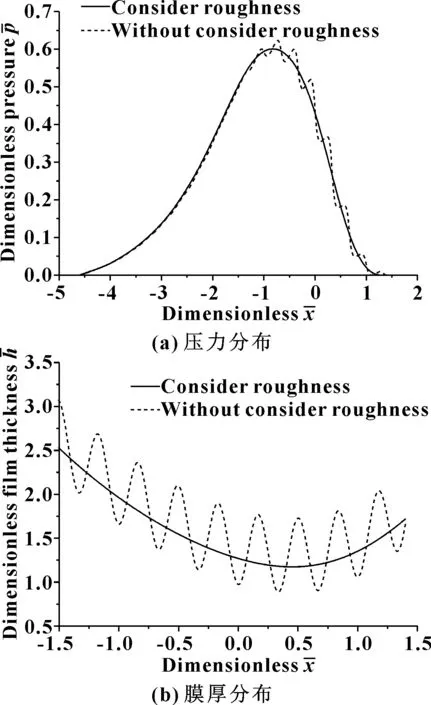
图5 考虑热效应时粗糙度对压力和膜厚分布的影响

可见,考虑表面粗糙度时的压力和膜厚，围绕理想光滑表面的压力和膜数值呈现余弦波动的特点，此时的变化趋势更加接近工程实际，所以有必要考虑表面形貌对磨削的影响。

4.3.2 粗糙度幅值对压力和膜厚的影响

图6示出了考虑热效应的工况下，粗糙度幅值(分别取0.5、1.0、2.0 μm)对磨削区压力和膜厚分布的影响。可见，粗糙度幅值对磨削区流体动压效应的影响表现在，幅值越大，波动越明显，并且整体压力增大，最小膜厚减小，但最大膜厚和平均膜厚增大。压力和膜厚分布都呈现出余弦波动的特点。

图6 考虑热效应时粗糙度幅值对流体动压效应的影响

4.3.3 粗糙度波长对压力和膜厚的影响

图7示出了不同粗糙度波长(分别取0.5、1.0、2.0 μm)对磨削区流体动压效应的影响。可以看出：粗糙度波长对磨削区压力的影响较明显，随波长增大，整体压力增大；但粗糙度波长对磨削区膜厚的影响不大，这主要和粗糙峰的疏密程度有关，所以粗糙度波长增加对润滑特性没有改善。但是在粗糙度幅值趋于无限小，粗糙度波长趋于无限大的情况下，砂轮和工件的表面形貌会接近于理想光滑表面的情况。

从图7中还可看出，不同粗糙度波长下压力分布和膜厚分布都呈现出余弦波动的特点。

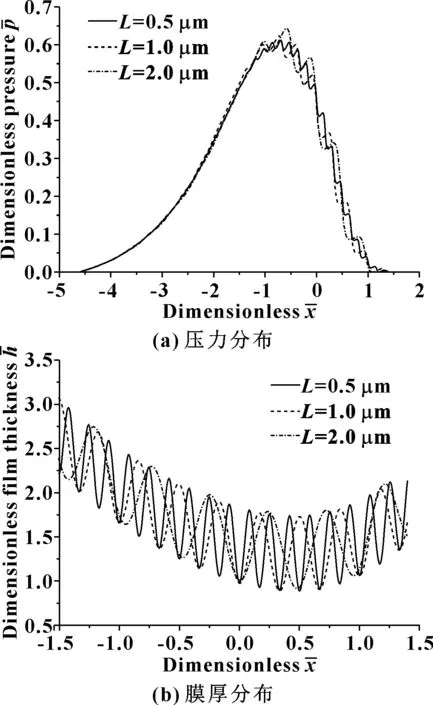
图7 考虑热效应时粗糙度波长对流体动压效应的影响

5 结论

(1)不同磨料的砂轮磨削时的效果不同，陶瓷刚玉砂轮磨削过程中的整体性能最优，整体膜厚最大，有利于减少非工作磨粒的磨损，降低磨削温度。

(2)热效应对砂轮磨削时的流体动压力和膜厚的影响比较大，考虑热效应时，磨削液的压力变小，膜厚变小，磨削过程中势必会有热产生，更符合工程实际，所以有必要考虑热效应的影响。

(3)表面形貌对砂轮和工件之间磨削液的压力和膜厚有很大的影响，是不可忽略的。考虑粗糙度时压力和膜厚呈现出余弦函数的波动情况，更接近实际；粗糙度的幅值越大，压力和膜厚波动越明显；波长对流体动压力的影响主要和粗糙峰的疏密情况有关，对流体动压力和膜厚的影响较小。