基于Abaqus的干气密封摩擦振动瞬时动态分析*
2019-08-02
(兰州理工大学石油化工学院 甘肃兰州 730050)
在干气密封环的开启和闭合阶段,由于槽所产生的动压不足,两密封面不可避免地产生干摩擦[1]。在对动静环进行摩擦试验的过程中,开启和停止及变载变速的情况下摩擦界面出现了剧烈的摩擦振动及噪声。目前,对于摩擦振动噪声的研究,涉及到诸多领域,如铁路机车制动[2-3]、汽车NVH[4-6]、石油勘探[7]等,但对于密封行业方面的摩擦振动的研究,国内外却少有报道[8]。除清华大学高志等人[9]的干气密封声发射研究报道外,几乎未见相关文献。
在摩擦振动噪声问题的研究中,有限元方法得到了广泛的应用。与试验方法相比,有限元方法既经济又高效,大大节省了研究经费与周期。该方法还可轻松将复杂的摩擦表面实体化,在设计和计算具有表面织构[10]或其他复杂表面的问题中有较大的优势。在此,本文作者借鉴汽车及机车制动领域有限元应用的成熟经验及研究成果,对干气密封动静环摩擦振动进行有限元仿真分析。
目前,对于摩擦振动噪声的有限元分析方法主要有2种:复特征值分析法[4-5,11-12]和瞬时动态分析法[2-3,10]。相比于复特征值分析法,近年来瞬时动态分析法得到了学者们的广泛应用,其包含各种非线性因素的影响,便于在分析中考虑各种状态及个监测点的时频信息。如有限元模型完善,瞬态分析法可得到与试验方法相对误差很小的结果[3]。王晓翠等[10]利用瞬态分析法设计并验证了织构界面在摩擦状态时对摩擦振动的影响。张立军等[13]基于Abaqus建立盘-销系统的瞬态动力学模型,预测了摩擦过程中制动盘及销的运动状态,并结合复模态和部件约束模态计算验证了其有效性。陈光雄等[2]利用瞬态分析法解决了地铁某路线的小半径曲线钢轨波磨问题。张明明等[14]利用复特征值法与模态分析法结合的方法,讨论了制动盘系统在特定情况下摩擦振动尖叫的规律。
根据干气密封动静环摩擦副的特点,本文作者采用瞬态分析法来讨论其启停阶段干摩擦状态下振动及噪声的相关规律,建立真实工况下的有限元模型,探讨干气密封摩擦振动规律。
1 双端面干气密封有限元模型
1.1 有限元模型
文中所研究的对象为双端面干气密封,其主要应用于介质为有毒有害、易燃易爆的气体场合及不允许有污染的食品加工和药物加工过程。
应用UG软件建立简化模型爆炸图如图1所示。其主要参数如表1所示。应用Hypermesh软件对模型进行结构网格划分,得到的网格模型如图2所示。该模型共有115 344个C3D8R网格以及112 640个节点,其中轴套网格数量为9 136,单枚动环网格数量为32 176,单枚静环为20 928。动环、静环及轴套的材料及性能参数如表2所示。

图1 双端面干气密封简化模型爆炸图
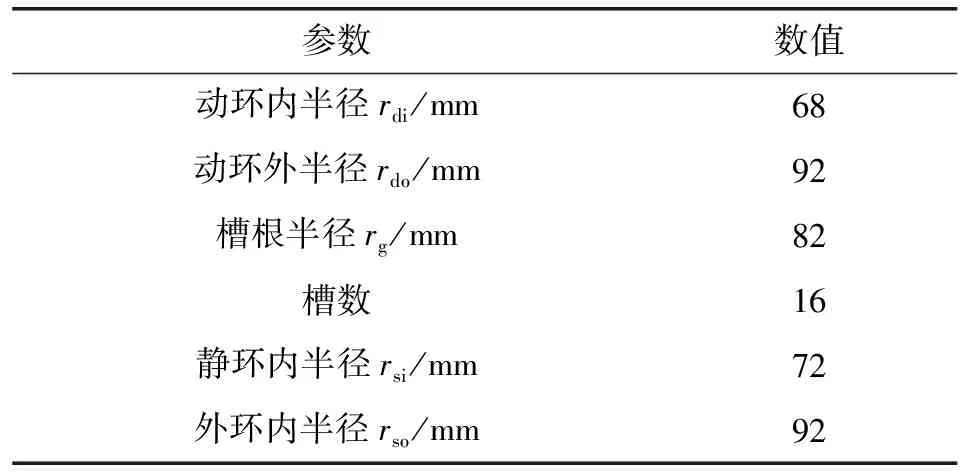
参数数值动环内半径rdi/mm68动环外半径rdo/mm92槽根半径rg/mm82槽数16静环内半径rsi/mm72外环内半径rso/mm92

图2 干气密封系统有限元模型
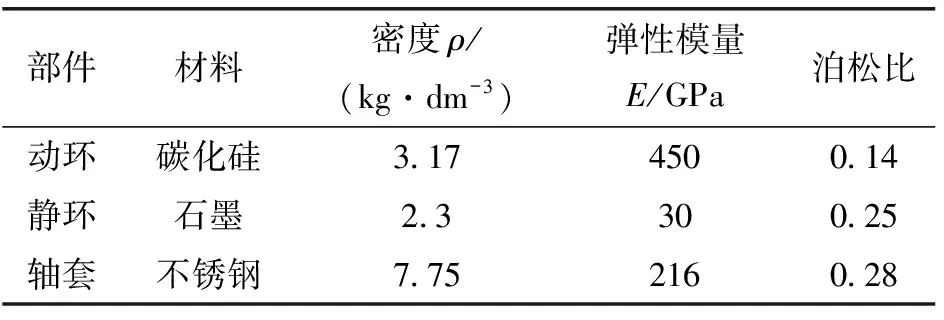
部件材料密度ρ/(kg·dm-3)弹性模量E/GPa泊松比动环碳化硅3.174500.14静环石墨2.3300.25轴套 不锈钢7.752160.28
1.2 瞬态分析
文中利用有限元分析软件Abaqus/Explicit动力学显示方法对模型进行分析,该方法应用中心差分法对运动方程进行显式地时间积分,其动力学平衡方程[15]为
(1)
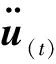
计算速度变化时设加速度为常数,利用前一个增量步中点的速度来计算当前增量步中点的速度值:
(2)

位移为
式中:u(t+Δt)为节点位移矢量。
根据采样定理,采样频率ωs必须大于被分析信号成份中最高频率ωmax值的两倍以上:
即:
只有满足此公式才能得到较为真实的信息。对于频率较大的信号,Δt的取值要足够小,但这也增加了Abaqus瞬态分析的时间。
1.3 基本假设
文中对该模型做如下基本假设:
(1)动环、静环、轴套均为各向同性材料,材料的物理参数不随时间的变化而变化;
(2)只考虑动环与静环之间的摩擦,且摩擦过程中符合库仑定律,既认为摩擦因数μ为常数,不随摩擦过程而改变,且忽略O形圈对摩擦过程的影响;
(3)忽略装置的结构阻尼、摩擦过程中的热效应以及材料磨损对摩擦的影响;
(4)干气密封在启停阶段由螺旋槽产生的动压力较小,所以仿真试验中忽略流体动压力对开启力的影响;
(5)由于文中忽略槽的动压效应,为了避免跨尺度划分网格,将动环螺旋槽槽深由微米级改为毫米级,此假设大大提高了计算效率,节省了计算时间。
定义干气密封仿真试验静环受力分析如图3所示,取合力并加载在静环表面上。动环和轴套采用Tie连接,约束轴套除绕轴旋转的其他5个自由度。定义密封压力为1 MPa,弹簧力为50 N,环境压力为标准大气压。摩擦因数设为0.2,施加速度约束为5 rad/s,检测加速度的节点设置在静环摩擦表面。
瞬态分析时间设定为0.06 s,按均匀间隔取6 000个时间节点数据。力与速度的加载历程曲线如图4所示。

图3 干气密封仿真试验压力分布

图4 密封闭合力与速度加载历程图
2 结果与分析
2.1 槽及槽深对摩擦振动的影响
为了探究动环槽深对摩擦振动的影响,分别提取槽深为5、2、1 mm情况下静环表面45314号节点时域信息,并对0.02 s后振动信号进行傅立叶变换,结果如图5所示。可以看出,动环螺旋槽槽深对摩擦振动信息影响不大,因此可基于文中提出的基本假设(5)来提高动静环摩擦过程的计算效率是可行的。
但无槽状况下的接触压力与有槽时不同,由于无槽的情况下其密封开启力随环的半径减小而单调递减,又有其接触面积的增加,所以在相同工况下两密封环间会产生更小的开启力。
无槽状况下节点法向振动加速度时域信息如图6所示,与图6(a)相比可知,在相同密封压力时无槽状况相比有槽时振动更加剧烈。2种情况接触压力对比如图7所示。
从图7中可以看出,不管是无槽还是有槽情况下在前0.01 s内接触压力升高较为稳定,但在0.01~0.02 s加速阶段,螺旋槽动环配对密封系统表现的接触应力出现较大的不稳定波动。这是由于螺旋槽区域旋转加速的能量积聚造成的,而无槽动环配对系统在该阶段应力波动较为稳定。在经历剧烈波动的加速阶段之后,有槽密封系统所表现的接触应力波动趋于稳定,波动幅度明显小于无槽情况。
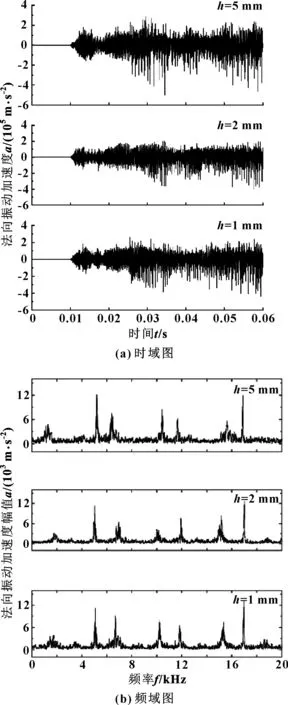
图5 不同槽深时频信息仿真试验结果对比

图6 无槽情况下时频信息仿真试验结果
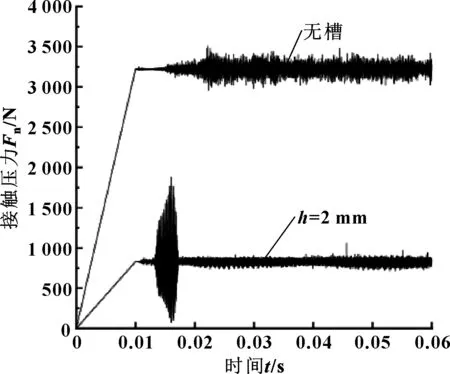
图7 有无槽时频接触压力结果对比
2.2 静环材料及摩擦因数对摩擦振动的影响
近年来干气密封动静环材料的选择及应用中出现了一种新型的“硬对硬”摩擦副设计,这种工程配对有效地降低了“软对硬”(石墨-SiC配对)摩擦引起的应力变形[16],但是也存在端面磨损严重等问题。文中采用SiC-SiC环模型对干气密封“硬对硬”摩擦副进行分析。图8所示为摩擦因数为0.2、槽深为2 mm时的时硬硬对摩时监测点的时域信息及表面接触压力历程。
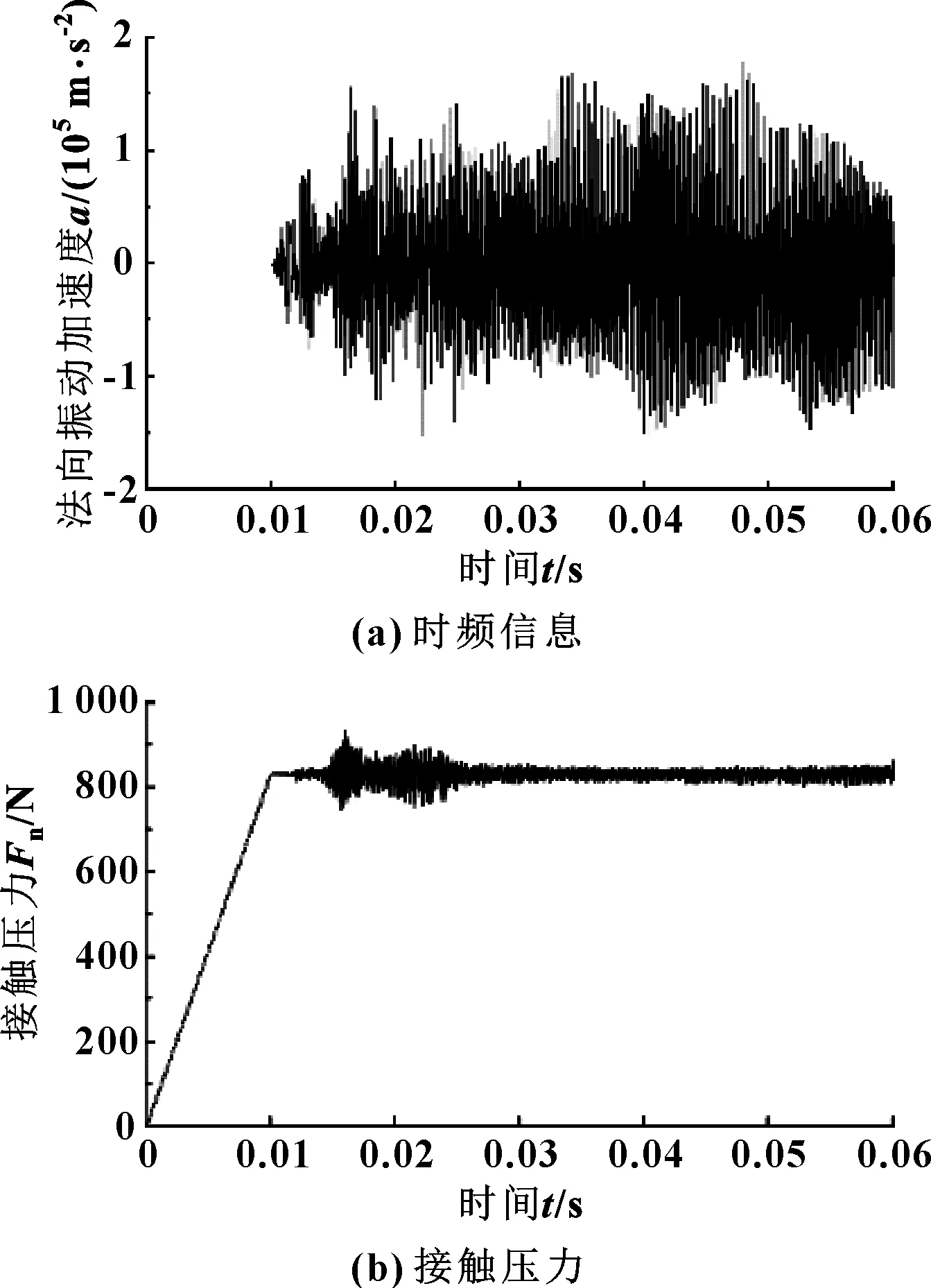
图8 “硬对硬”接触摩擦副振动加速度、接触压力时间历程(μ=0.2)
对比图8(a)及图5(a)所示的槽深2 mm下的时域图的可以看出,当摩擦因数相同时,“硬对硬”较“软对硬”配合下的摩擦副振动幅度有小幅度降低,而比较图8(b)和图7可知,硬硬摩擦状态下的接触压力在动环加速转动时表现出更小的波动。可见,对于摩擦状态下振动性能来说,双SiC环配对要明显优于SiC环与石墨配对。
为了提高端面的摩擦学性能,行业上对静环表面采取镀膜技术。具有表面薄膜的摩擦副滑动时,黏着点的剪切发生在膜内,其剪切强度较低。又由于表面膜很薄,实际接触面积则由硬基体材料的受压屈服极限来决定,实际接触面积又不大,所以合理的镀膜可以有效地降低摩擦因数[17]。假设薄膜对摩擦振动无影响,分别再对摩擦因数为0.1、0.08、0.06情况进行计算。为对比密封系统干摩擦状态下不同摩擦因数下的平均振动幅度的大小,对0.02 s后的离散信号求解均方根值,如图9所示。
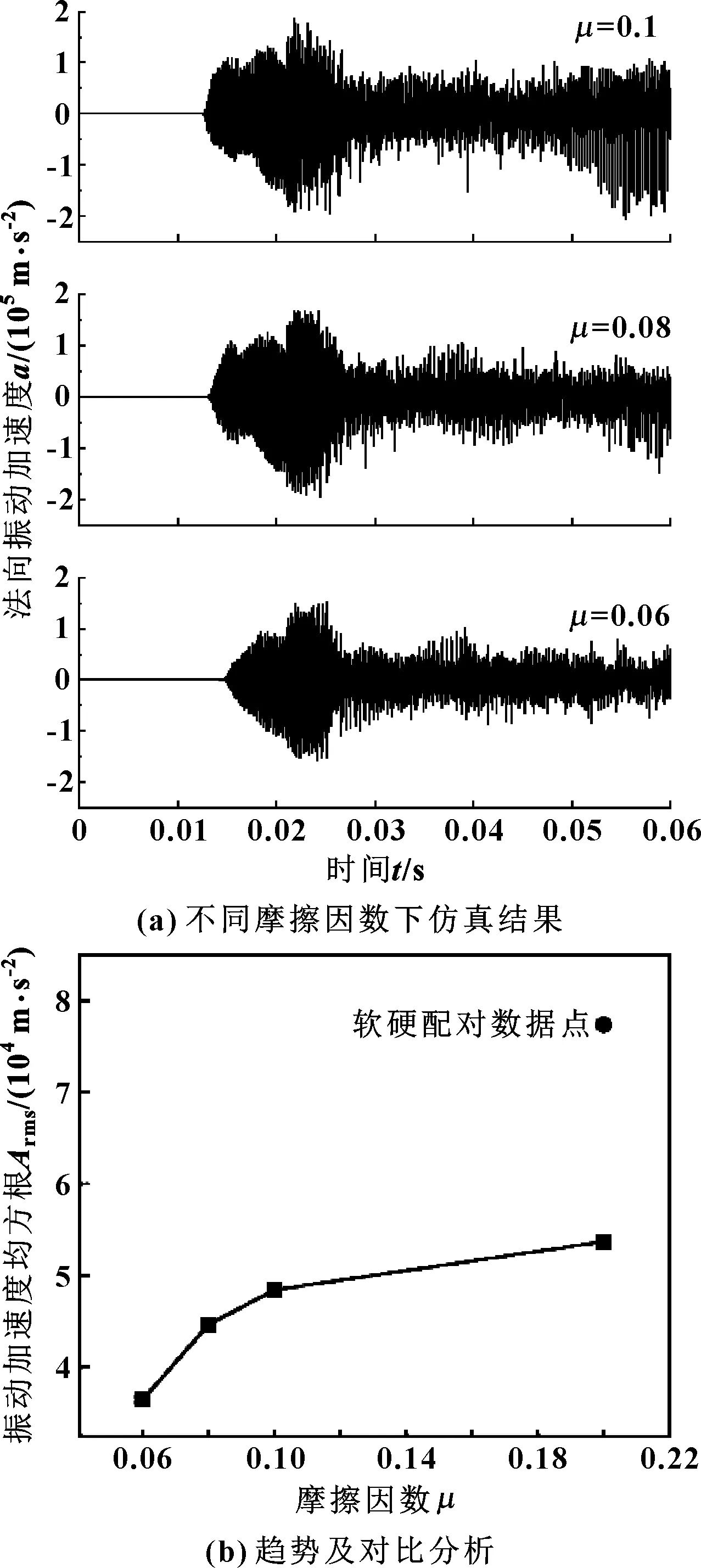
图9 “硬对硬”情况下不同摩擦因数时仿真分析结果
当摩擦因数减小时,相应的摩擦振动幅度也会随之降低。当摩擦因数由0.2降为0.1时,相应的振动加速度均方根有小幅度下降(降幅为0.1时,均方根减少大约为4%);但当摩擦因数降为0.1以下时,振动均方根随着摩擦因数的减少大幅度降低(在下降幅度仅0.02时,其均方根减少大于10%),在图9(b)中表现出的斜率更大。从图9(a)中可以看出:摩擦因数为0.1时,“硬硬”配对在运行0.05 s后出现不稳定振动阶段,随着摩擦因数减小到0.08时,不稳定阶段振幅降低;当摩擦因数等于0.06时,不稳定振动阶段消失。由此可知,尽可能低的摩擦因数对降低摩擦振动波动幅值有很大作用。
图5(a)中槽深2 mm下的摩擦时域信号的均方根值的计算结果为7.73×104m/s2,较相同状态下双SiC摩擦系统均方根值大44%左右。膜的作用间接地提高了密封环的防振性能,但“硬硬”配对在加速阶段表现出的高量级振动也不容忽视。这可能是导致干气密封镀膜脱落的主要原因,也是今后探索研究的重点。
2.3 不同槽形对摩擦振动的影响
T型槽(T-DGS)干气密封由于其端面槽型对称,能适应双向旋转,而被广泛地应用于石化、化工等行业用高速旋转设备上。在相同工况下,对相同槽数、动压槽根半径、摩擦接触面积的T型槽进行分析,其均方根对比如表3所示。可以看出,在相同摩擦因数、接触面积相近的情况下,T型槽动环摩擦系统相对经典螺旋槽(S-DGS)来说,静环监测点的法向加速度振动均方根要小大约20%,T型槽相对经典螺旋槽来说,具有较优越的摩擦振动性能。仿真结果可为今后试验及工程应用提供参考。
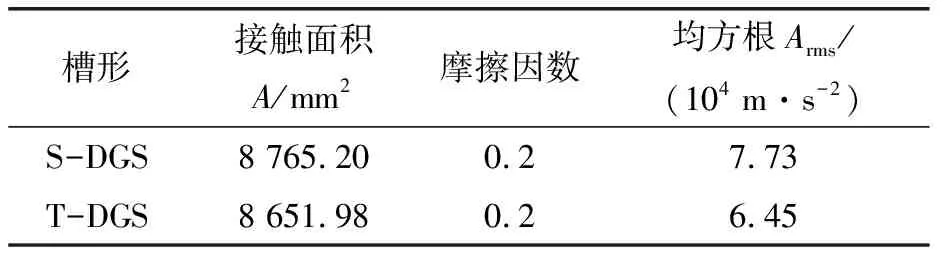
表3 槽形参数及RMS对比
3 结论
(1)通过对比槽深为5、2、1 mm情况下静环表面监测节点时频信息可发现,干气密封动环槽深对摩擦振动的影响不大,依此假设建立的仿真研究具有可靠性。在同一密封压力下,动环带有槽的摩擦副振动幅度要明显大于无槽情况。
(2) 双SiC“硬对硬”密封环配对要明显优于SiC与石墨“软硬”配对,但在转速增加时会出现振幅大幅度波动现象,这将是今后研究的重点。摩擦因数对密封环摩擦振动也具有较大影响,通过对双SiC环不同摩擦因数的计算发现,当摩擦因数减小时,系统产生的不稳定振动会有明显的降低。
(3) 在工况相同且动压槽根半径、摩擦接触面积相近时,带有T型槽动环的摩擦副较经典螺旋槽摩擦副表现出更好的摩擦性能。
