基于容错卡尔曼滤波的校验无人机精确测高法

胡丹丹，顾 圆，高庆吉

（中国民航大学电子信息与自动化学院，天津 300300）

精密进近航道指示器（PAPI，precision approach path indicator）系统是为进近着陆中的飞机提供正确下滑航道的助航灯光系统，能够在飞机降落过程中为飞行员提供正确的下滑航道指示信息和不同的偏离指示信息。机场在灯具安装设置完成后，会在首次投入使用之前和规定的维护周期间隔对PAPI 系统的仰角进行飞行校验[1-3]。目前PAPI 系统的飞行校验都是由驾驶员驾驶满足飞行校验要求的民航客机并携带相关设备完成[2]，采用真实飞机实施人工校飞的方法操作过程繁杂、牵扯部门多，存在校验成本较高、时间耗费多等问题。因此，采用无人机替代飞机对PAPI 进行自主校验逐渐成为一种趋势。

机场设计手册中规定应纠正大于1′的PAPI 灯具仰角角度误差[2]，通过校验原理及计算分析可知，无人机以距PAPI 一定水平距离定点水平校验时，其校验误差等于高度测量误差，因此，旋翼无人机高度测量精度是决定PAPI 角度校验误差的关键。

胡永红[4]提出采用卡尔曼滤波对气压高度计、全球定位系统（GPS）和线加速度信息进行融合，并根据测量信息的冗余设计了系统的故障检测和隔离算法，但仿真实验忽略了动态情况下的误差特性。Drak 等[5]提出一种基于卡方检测的检错隔离的高度信息融合测量方法，该方法直接以各传感器融合高度状态量作为参考量，对各传感器的测量状态量进行故障检错。

根据旋翼无人机校验PAPI 灯实际应用需求，采用惯导在短时间内二次积分量作为参考信号，通过检错器进行状态卡方检测与残差卡方检测，得到不同传感器的故障系数及权重系数，将该有效高度数据融合得到精准高度信息。最后，将该方法应用于校验无人机飞行校验中并验证该方法的有效性和精确性。

1 容错卡尔曼滤波的设计

以卡尔曼滤波器输出的估计误差及高度误差作为测量量，以惯导在短时间内二次积分的估计误差及高度误差为检错器参考量，通过检错器对各传感器测量信息进行检错隔离，如图1所示。

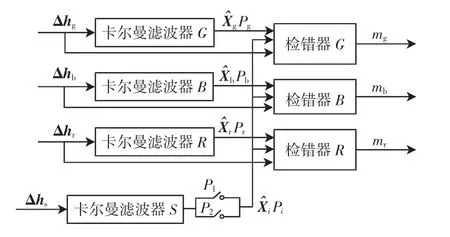
图1 容错卡尔曼滤波方法示意图Fig.1 Schematic diagrams of fault-tolerant Kalman filtering method

1.1 KFT 滤波算法

文中所涉及每种卡尔曼滤波都是标准的，以卡尔曼滤波G 为例。卡尔曼滤波的状态矢量可表示为

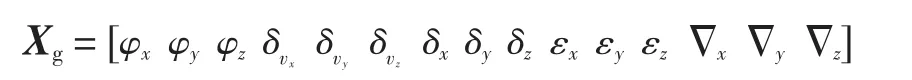
其中：φx、φy、φz为姿态误差；δvx、δvy、δvz为速度误差；δx、δy、δz为位置误差；εx、εy、εz为加速度测量误差；Δx、Δy、Δz为角度测量误差。

假设k 次真实状态由k-1 状态演变而来，卡尔曼滤波器G 模型[6]描述如下

其中：Fg，k为k 时刻组合高度测量系统状态转移矩阵Xg，k-1的状态转换模型；Wg，k为k 时刻系统噪声。

卡尔曼滤波器G 的测量向量可表示为在k 时刻，真实状态X 的观察量可表示为

其中：H 为将真实状态空间映射到观察空间的观测矩阵；V 为观察噪声，在卡尔曼滤波中，假定V 为期望为0、协方差为R 的高斯白噪声。

卡尔曼滤波G 的方程[6]可表示为以下3 部分：

1）预测

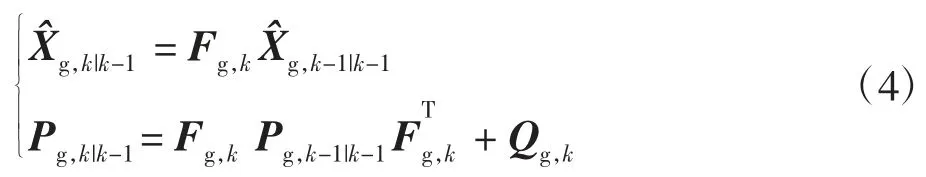
2）更新

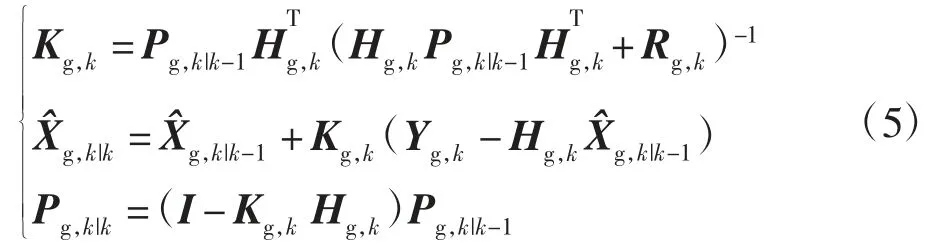
3）状态递推

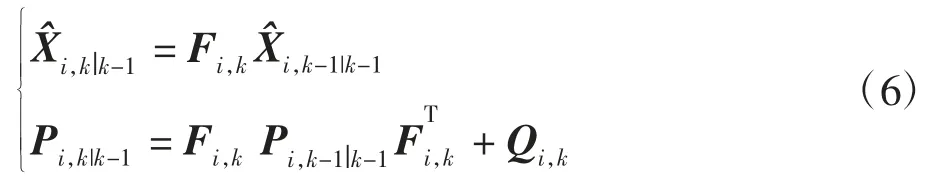
其中：P 为状态预测的误差方阵；Q 为过程激励噪声协方差阵；R 为测量噪声协方差阵；I 为单位矩阵；i 为状态递推器下标，i=1，2。

1.2 容错KFT 滤波算法

测试检查信号与参考信号间一致性的卡方测试，广泛应用于随机动态系统的故障检测。根据测试统计使用方法的不同，卡方测试可分为3 类：残差卡方检测、具有一个状态递推器的状态卡方检测和具有两个状态递推器的状态卡方检测。

由于卡尔曼滤波器的状态向量都相同，只能采用带有两个状态递推器并行结构的状态卡方测试和残差卡方测试的故障检测器来增加运算速度，如图2所示。如果状态卡方测试或残差卡方测试检测到故障，则mg=0，否则mg=1。检验统计量服从卡方分布，故障检测是

其中，εd的阈值由错误警告率决定。

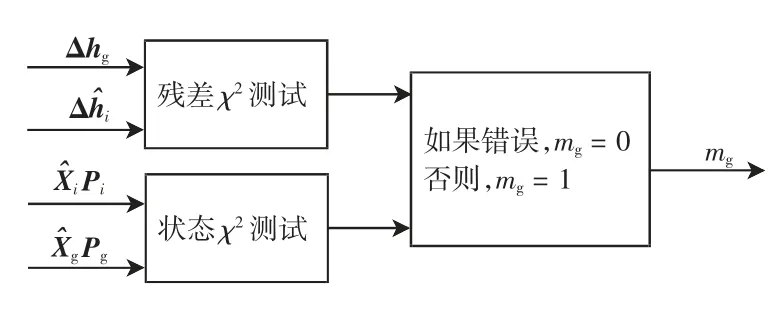
图2 传感器故障检错器结构示意图Fig.2 Structure diagram of sensor fault detector

2 容错卡尔曼滤波的校验无人机测高法

校验无人机采用气压计、声呐、GPS 和捷联式惯导（IMU）同时进行高度测量，信息高度融合控制回路结构图[7]如图3所示。通过容错卡尔曼滤波器，得到各传感器的可信度，再对可信度分配适当权值进行数据融合，最后获得一个最优高度信息。

图3 高度数据融合控制回路结构图Fig.3 Structure diagram of height data fusion control loop

各传感器的输出权值可根据每个传感器输出高度误差计算得出，如GPS 传感器的权值计算如下

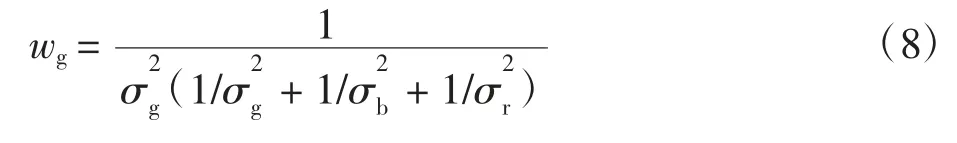
其中：σg为GPS 传感器输出误差的方差；σb为气压计输出误差的方差；σr为声呐传感器输出误差的方差。而融合后的最佳高度为

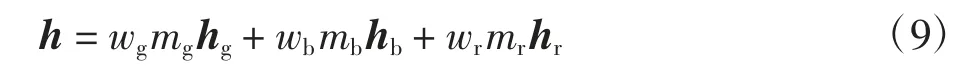
其中：w 为各个传感器测量数据的权值系数；m 为各个传感器的故障系数，若某传感器的某数值报错则该值为0，否则为1；hg、hr、hb为各传感器的测量高度。高度测量方法如图4所示，算法步骤如下。

步骤1计算高度状态估计值与误差值。采用卡尔曼滤波算法分别计算各传感器输出高度误差的状态预测值、估计值及不同高度的误差值。

步骤2计算传感器的故障系数。根据步骤1 得到的高度估计值与误差值，采用卡方检测原理，分别对不同传感器高度值进行残差卡方测试与状态卡方测试，得到不同传感器的故障系数。

步骤3计算传感器的权重系数。结合不同传感器的输出高度值，计算高度误差方差，然后根据不同传感器的误差方差计算传感器的权重值。

步骤4最优化高度融合。结合步骤2、3 以及传感器的输出高度值进行融合计算，得到容错卡尔曼滤波数据融合后的测试高度。

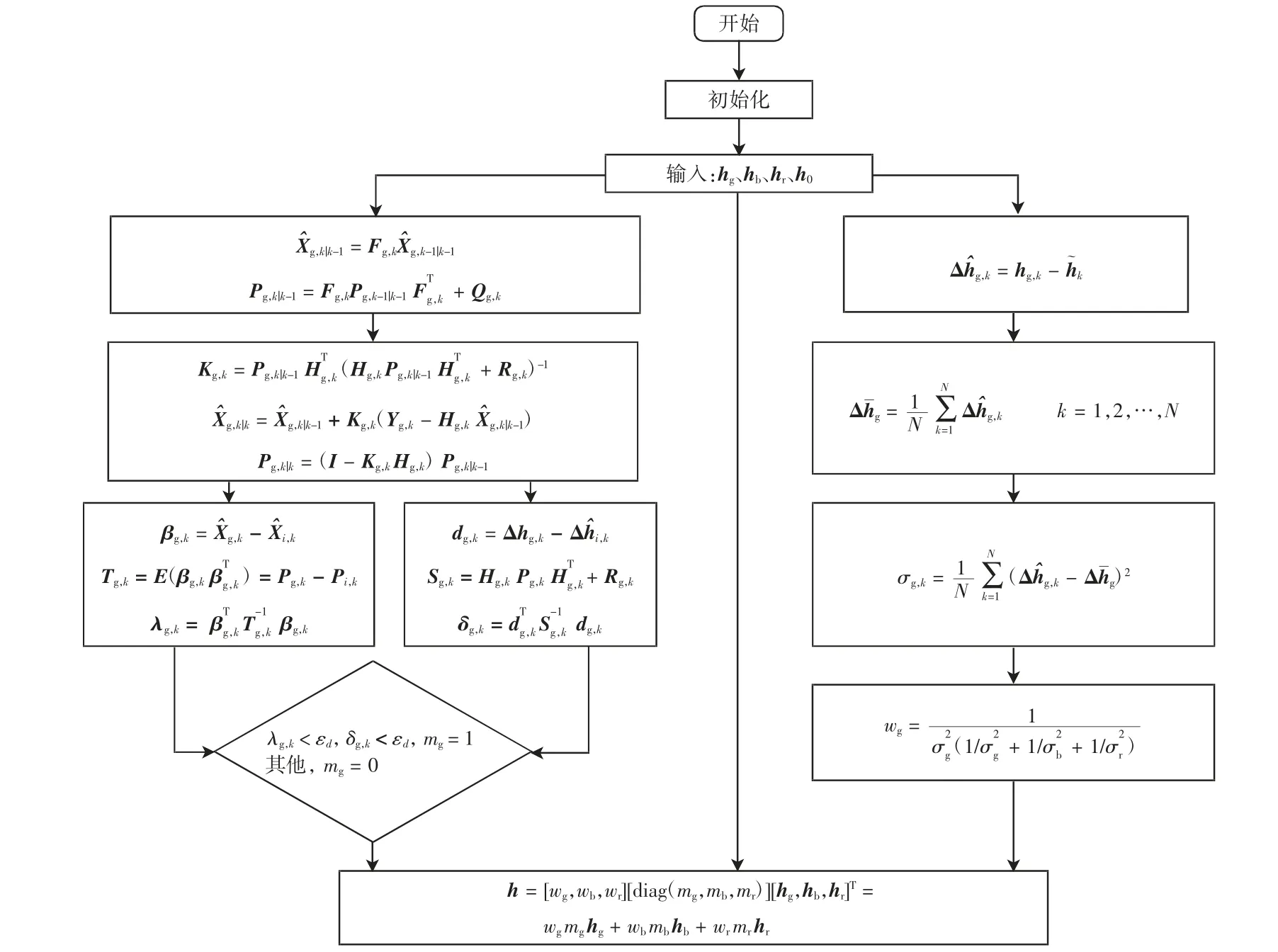
图4 高度信息融合算法示意图Fig.4 Flow chart of high-level information fusion method

3 实验验证

3.1 高度信息融合仿真

设初始状态特征向量X=[0.02]，表示高度误差，定高飞行各时刻状态的高度误差基本一致，因此令状态转移矩阵Fg=[1]，系统测量矩阵Hg=[1]，初始协方差P0=0.4，过程激励噪声协方差Q=0.000 1。

针对GPS 传感器发生故障进行仿真验证。仿真各传感器信息如图5（a）所示。根据权值计算公式计算各传感器仿真数据权值，分别为wg=0.072 1，wb=0.902 1，wr=0.025 8，经容错卡尔曼滤波数据融合后的仿真结果如图5（b）所示。

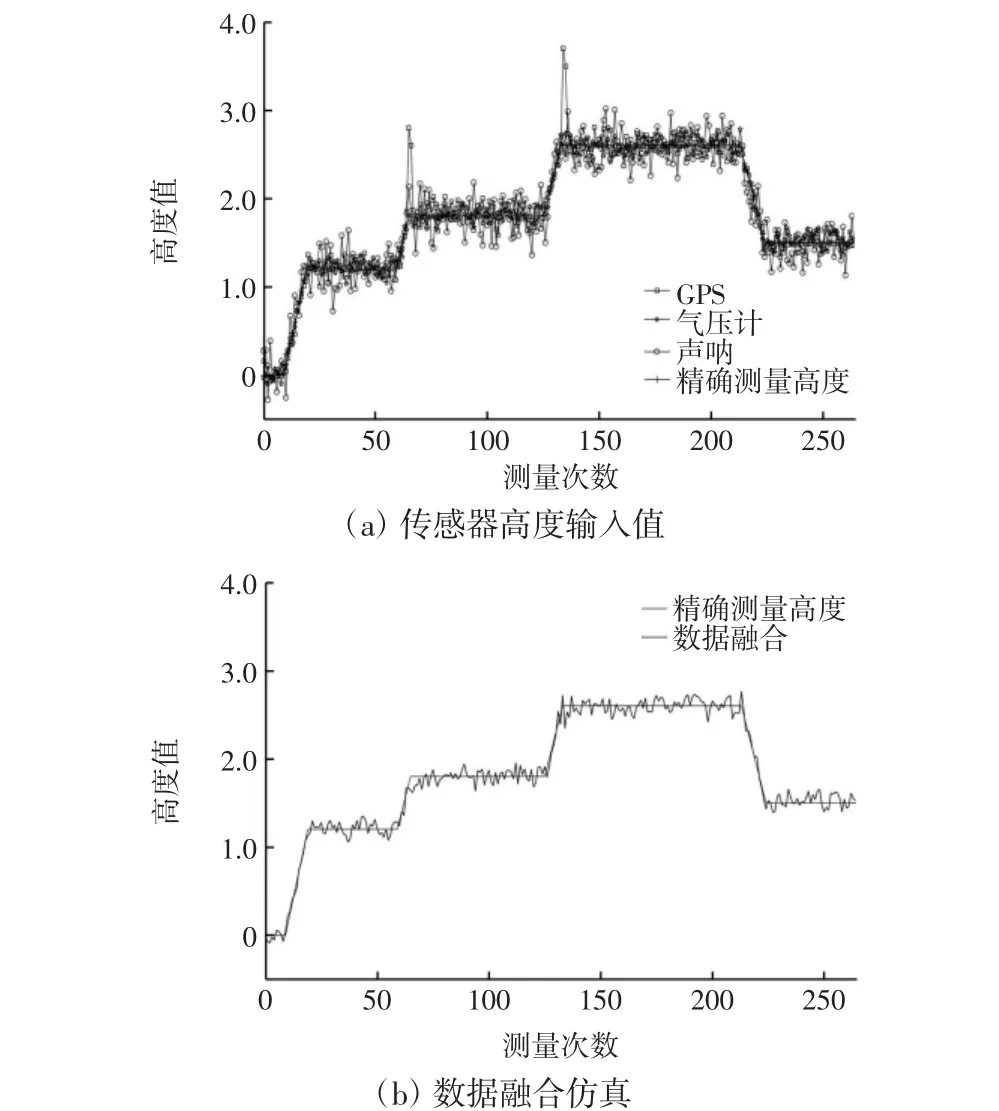
图5 测高系统仿真结果Fig.5 Simulation results chart of height measurement system

对比图5（a）和图5（b）中数据融合前后的高度值，经过容错卡尔曼滤波算法处理融合后的输出数据更接近精确测量值，且对中间GPS 传感器的某一错误数据能够准确定位并剔除，实现了系统的实时在线检错与错误隔离。

为进一步验证该算法的融合精度，对GPS、气压计、声呐及数据融合的4 组数据进行误差分析，误差曲线如图6所示，数据融合后的高度误差值曲线如图6（b）所示，GPS 传感器局部测量误差较大，但融合误差在期望范围内。

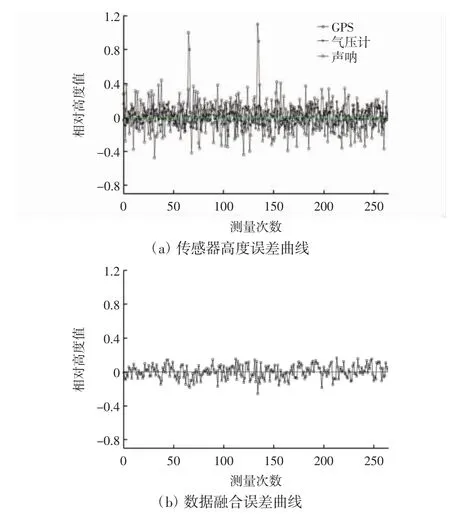
图6 高度误差曲线Fig.6 Height error graph

为更直观的观测各组误差信息，各传感器的误差均值与方差，如表1所示。从均值角度看，GPS 传感器有两个故障数据，该传感器误差均值较大即该传感器测量数值波动较大。从方差角度看，卡尔曼滤波数据融合后的误差方差最小，测量波动性更小。

表1 各传感器误差均值及方差Tab.1 Error mean and variance of each sensor

综上所述，容错卡尔曼滤波数据融合结果比单独一个或多个卡尔曼滤波融合得到的数据可靠性更高。

3.2 飞行试验及结果分析

基于自行设计的旋翼飞行器平台进行实验。场景如图7所示。

图7 旋翼校验无人机平台Fig.7 Rotorcraft verification UAV platform

旋翼飞行器平台上面搭载了惯性导航系统、mb1212 声呐、mb1212 气压计及UBLOX GPS。使飞行器分别在1.2 m、1.8 m、2.6 m 和1.5 m 左右采用定高模式飞行。

在飞行过程中改变定高目标值，实现平台式定高试验，可看出多传感器高度信息在容错卡尔曼滤波法融合后，高度信息更加平稳，如图8所示。

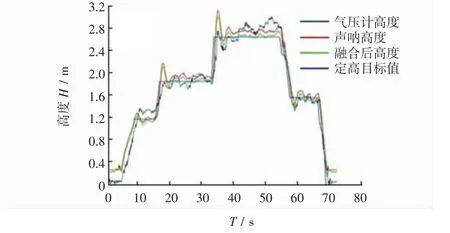
图8 数据融合高度信息Fig.8 Data fusion height information

图9采用容错卡尔曼滤波融合法融合定高飞行高度数据在第24 s 时给声呐一个短暂的平台干扰，可看出融合后的高度信息没有发生大幅度突变。

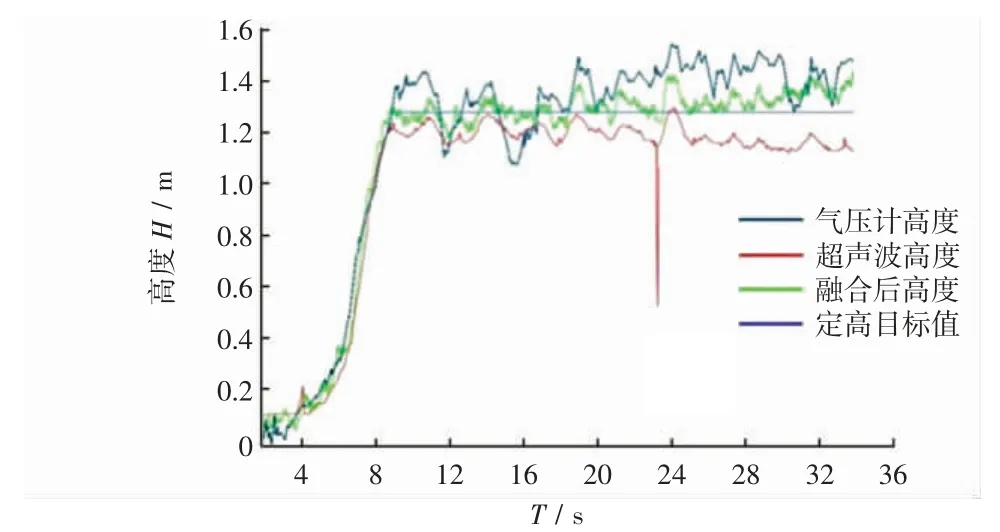
图9 旋翼无人机定高飞行Fig.9 Rotorcraft UAV set high

从图10 中高度误差曲线可知，融合算法计算后的高度值更接近于真实高度。此外对3 组数据的方差与均值进行计算与分析，计算结果如表2所示。融合后的数据均值与方差最小，说明融合后的数据波动性最小、精度高，得到的数据更稳定，且高度误差为0.1～0.5 m，可达到校验无人机飞行校验精度。

表2 各传感器误差均值及方差Tab.2 Error mean and variance of each sensor

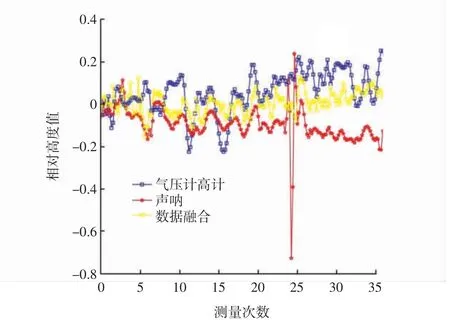
图10 高度误差曲线Fig.10 Height error graph

4 结语

针对旋翼无人机在飞行校验过程中遇到各种干扰，使某个测高传感器的数据发生突变的问题，提出了卡方波状态检错和卡尔曼滤波器结合，进行在线故障检测和错误隔离，得到可信度后再对其进行数据融合的高度测量方法。通过仿真与实验，验证了该方法的有效性。虽实验与仿真结果有一定误差，但其测量精度与稳定性可满足校验需求。