基于“探究性学习”初中数学课堂实践与思考
——浙教版八上2.7探索勾股定理教学实践
2019-08-01李静
李 静
(浙江省嘉兴市海盐县滨海中学,浙江 嘉兴 314300)
探究性学习是一种有别于传统教学的学习模式,是以“培养学生永不满足,追求卓越的态度,培养学生发现问题,提出问题,从而解决问题的能力”为目标的自主学习模式。它是一种实践性很强的教育教学活动,有助于学生提高参与学习的热情和积极性,能让学生从探究中主动获取知识,应用知识,解决问题。探究性学习是新课程倡导的一种学习方式,非常适用于初中数学学科。本文结合浙教版八年级数学上册2.7“探索勾股定理”的课堂教学,就“基于学生的自主探究,促进学生自觉生成新知,促进学生主动发展,涵育数学素养”阐述其立意和做法,与大家共同探讨。
一、在探究中导入新知——导趣启思
俗话说的好,好的开端是成功的一半。课堂导入环节是一节课的关键之所在,我们如果要开启探究模式,就要激发学生参与探究的兴趣,并在兴趣的引领下,触发学生参与探究的思维。兴趣与思维双管齐下,才能让探究在课堂教学中发挥理想的效果。
片段一:创设情境,引入新课
问题情境:2002年世界数学家大会在我国北京召开,投影显示本届世界数学家大会的会标:会标中央的图案是一个与“勾股定理”有关的图形,数学家曾建议用“勾股定理”的图来作为与“外星人”联系的信号.
师问:你见过这个图案吗?
生:我在数学课本的封面上见过。
生:我在小学的奥数课堂上见过。
生:我在数学资料书上见过。
师问:非常好,看来大部分同学都见过这个图案,在这幅图案中有哪些我们熟悉的图形呢?
生:正方形,直角三角形
师问:你从图中能获取到什么信息?你想知道这张图暗藏的玄机吗?
思考: 在本次活动中,教师发现学生对“赵爽弦图”及勾股定理的历史非常感兴趣,学生对勾股定理的有一定的了解。教师用“赵爽弦图”创设了问题情景,引导学生积极主动地投入到探索活动中,激发了学生学习热情,同时为探索勾股定理提供背景材料。教师引导学生阅读图形语言,用问题吸引学生,激发学生探索的欲望。

二、在探究中生成新知——建知启智
每个学生都是一个独立的个体,都有自己的独特的思维方式。教师理应巧妙的应用这一点,为学生搭建自由学习的平台,设置有效的探究活动,让学生在活动中体验学习的乐趣,增强人生智慧。在数学教学中,教师通过组织引导学生们开展探讨交流活动,引领学生在互动探究中学习,促进知识的自然生成,启发学生的智慧。这一过程不仅构建了新的知识和技能,更启发了学生的思维方式,提升了学生的智力水平。片断二:合作交流 形成新知
师问:从图形的构造来看这幅图,你能用一句话来描述这个图形吗?
生:直角三角形拼出正方形。(开始渗透图形语言与文字语言的转化)
师问:你能拼出这个图形吗?小组合作试试看。
(教师深入小组,参与学生交流,关注学生的参与程度、动手能力、合作意识,以及在研究过程中表现出的思维水平。通过发放小组得分卡的方式,引发学生兴趣。及时对小组的完成情况及参与度进行评价,提高了学生的积极性,避免小组合作流于形式。)
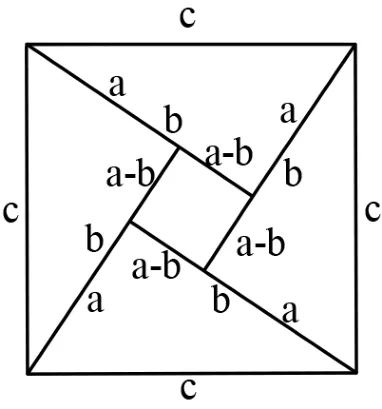
师问:这幅图中最基本的图形是什么?
生:一个小正方形和四个全等的直角三角形拼成一个大正方形。
师:非常好,我们学数学一定要注意语言的准确性。
师问:你能用最少的字母把这幅图中所有线段表示出来吗?
教师强调“所有线段”,引导学生往既定方向思考,
为后面等式的列出埋下伏笔。
师问:你能通过这幅图找出一些等量关系吗?
生:四个全等的直角三角形面积加小正方形的面积等于大正方形的积。
师:这个同学的语言表达非常准确!你能用等式表示吗?
生:4S△+S小正方形=S大正方形
师问:通过引入字母找出的等量关系,你可以得出什么结论?
师问:你能用一句话概括刚才得到的结论吗?
生:a2+b2=c2
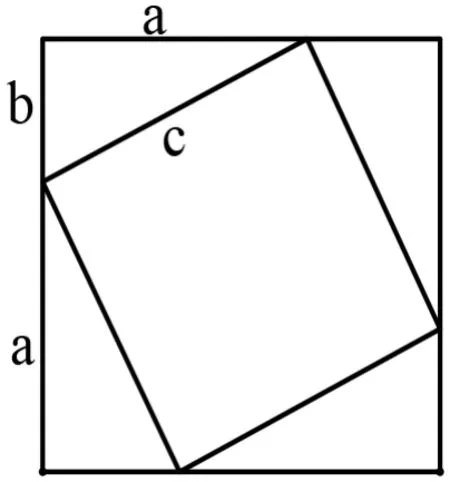
师问:你能用这四个全等的直角三角形拼成与弦图不一样的图吗?
师问:仿照刚才的思路,你能否得出相同的结论?
生:4S△+S小正方形=S大正方形
思考: 拼图活动,调动了学生的积极性,为学生提供从事数学活动的机会,让学生建立初步的空间观念,发展形象思维,使学生对定理的理解更加透彻,对数学中数形结合思想的体会更加深刻。这一探究活动,充分调动学生的积极性,激发学生探求新知的欲望。活动中教师给学生充分的时间与空间讨论和交流,鼓励学生敢于发表自己的见解,让学生感受合作的重要性。
三、在探究中应用新知——析知用智
新课程标准强调:“让学生学会有价值的数学,获得必需的数学,让不同的学生在数学上得到不同的发展,人人能够应用所学知识解决生活中的实际问题”学习知识就是为了应用知识解决生活中的实际问题。在知识和技能已经掌握的情况下,教师需要引导学生在现实生活中探求应用,构造用数学模型解决实际问题的意识和能力。让学生在探究中感受数学的魅力,体会数学的价值,在实践中提升学生的综合能力,促进学生的智力生长。
片段四:灵活应用 巩固提升
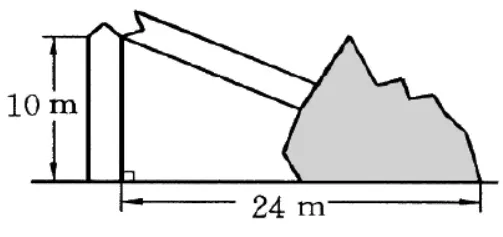
例.如图所示,一棵大树在一次强烈台风中于离地面10m处折断倒下,
树顶落在离树根24m处. 大树在折断之前高多少?
师问:没折断的树干与地面及折断的树顶构成什么图形?
生齐答:直角三角形
师问:欲求大树在折断之前高得先求什么?
生:折断后的树顶长度。
师问:怎么求树顶的长度,需要用到什么知识来解决这个问题?
生:勾股定理(师请同学们先独立完成在练习纸上,再请一名同学板演交流)
思考: 对数学知识的应用是建立在对数学概念充分理解的基础上的思维活动,只有对数学数学概念深刻理解,才能提高学生的解题能力,应用能力。这两道题目都是为了巩固本节课所学知识而设计的基础练习,可以更好的让学生理解勾股定理,同时也让学生明白了勾股定理是一个数形结合的定理,它广泛的应用于我们的实际生活中,是一个非常重要的定理,学它是为了更好的用它来解决实际生活中的问题。
四、在探究中拓展新知——用知生智
数学知识的有效掌握,有赖于学生积极主动的探索。学生只有通过教师的问题引领,提出问题,选择方法,解决问题,才能有效地建立新的认知结构,理解并掌握新知。数学知识从理解到掌握需要一个循序渐进的过程,在这个过程里,教师要通过一系列的问题串,由易到难,由浅入深,带领学生从知识的表象步步深入探索到知识本质。教师反馈过程中呈现的问题进行点拨、分析,以此来促进学生对新知掌握的深度和广度,培养学生用智慧来感悟数学的方法与技巧。
片断三:拓展延伸,体验成功
师:阅读以下数学小史,提出自己的疑问,课后自己查资料解决。
1.勾股定理是我国最早发现的,中国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦,“勾股定理”因此而得名。
2.在西方称勾股定理为毕达歌拉斯定理。约公元前500年,毕达歌拉斯学派的弟子希帕苏斯(Hippasus)发现了一个惊人的事实:一个正方形的对角线的长度是不可公度的。若正方形边长是1,则对角线的长不是一个有理数,它不能表现成两个整数之比。这一事实不但与毕氏学派的哲学信念大相径庭,而且建立在任何两个线段都可以公度基础上的几何学面临被推翻的威胁,第一次数学危机由此爆发。
师问:勾股定理的本质是什么?
生:直角三角形三边的关系。
师问:你们已经了解了直角三角形中的什么关系?
生:1.角的关系(两锐角互余) 2.边的关系(勾股定理)
师问:你们还思考了什么问题?有没有同学想问我什么问题?
生:我想知道直角三角形中边与角之间有什么关系。
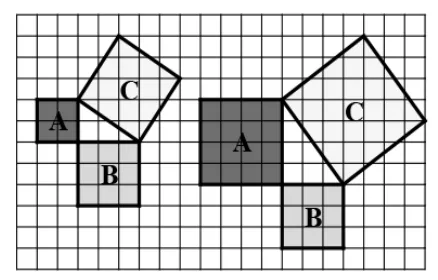
师问:(1)观察下面两幅图:
你能得到正方形C的面积的?与同伴交流.
师:我们可以把它理解为勾股定理的几何意义。
师问:大家还可以构造出类似的图形吗?
思考: 教师指导学生阅读勾股定理,了解勾股定理的重大意义和文化价值,体会世界文明的进步与发展,进一步激发学生的学习兴趣。通过一系列的问题串,层层递进,带领学生由图形的表象步步深入探索到本质。引导学生学会深入思考,启发学生学会发现问题,鼓励学生提出问题。教师以基本图形为背景,对相关问题进行了整合与深化,提升了学生对基本图形的理性认识,开拓了学生的空间思维能力,同时也发展了数学思维的深刻性、灵活性及创造性。
探究性学习,不仅仅是数学知识的探究,更能解答学生思维中的困惑,带领学生构建新的认知和技能,引发学生感悟新的数学思想和理念,全面促进学生智力能力的提升,涵育学生的数学素养。开展探究性学习,不仅是为了适应新课程改革的需要,更是为了培养学生主动参与学习的意识,培养学生应用知识解决实际问题的能力,是真正实现素质教育的需要。
