地外天体起飞羽流导流气动力效应仿真
2019-07-31苏杨蔡国飙舒燕叶青张明星贺碧蛟
苏杨,蔡国飙,*,舒燕,叶青,张明星,贺碧蛟
(1.北京航空航天大学 宇航学院,北京100083; 2.北京空间飞行器总体设计部,北京100094;3.北京航天长征飞行器研究所,北京100076)
探测器完成地外天体表面任务后,起飞器负责携带相关设备脱离地外天体。起飞器在起飞过程中,发动机喷出的羽流与起飞平台表面作用后反向流动至起飞器表面,会对起飞器产生明显的气动力效应。这一羽流导流气动力效应会对起飞过程中起飞器产生力矩作用,对其姿态控制和保持产生影响,可能导致起飞器无法正常工作或者工作质量下降。因此,对地外天体起飞过程中起飞器及起飞平台可能受到的羽流导流气动力效应进行研究十分必要[1-2]。
目前成功实现月面起飞的国家只有美国和俄罗斯,由于相关数据的保密性,仅有少数文献对Apollo登月舱下降级的凹碗型导流装置的导流效果进行研究[3]。国外对羽流导流效果研究方面多关注于大气环境下火箭起飞过程,关注点主要集中于导流机构受到的热效应及声载荷影响等[4-8]。中国自2013年成功实现嫦娥三号探测器月面软着陆及月面巡视以来,相继开展了地外天体起飞羽流导流气动力热效应的实验研究和仿真研究。贺卫东等[9-12]在高超声速低密度风洞中,利用氮气为工质,设计了1 ∶10缩比模型的羽流导流实验,并对平板、凹槽和锥面的羽流导流机构的导流效果进行了实验和仿真验证。张明星等[13]在真空羽流实验系统中模拟了真空环境,针对起飞器与锥形导流机构在不同距离、不同偏转角度工况下起飞器受到的羽流导流气动力效应开展缩比实验研究,并与仿真结果进行了对比。张萃等[14]对导流机构受到羽流冲击后的热载荷进行了分析。虽然研究人员对地外天体起飞羽流导流效应进行了相关的缩比实验研究和仿真研究,但是对大尺寸起飞器所受到的羽流导流气动力效应研究并不充分。此外,由于受到着陆过程振动或天体表面不平整影响,起飞器在起飞平台表面可能存在初始偏角,或在起飞过程中需要进行姿态调整。因此,起飞器起飞过程中,随着上升距离和偏转角度的改变,需对引起的羽流导流气动力效应变化规律进行深入研究。
本文利用计算流体力学/直接模拟蒙特卡罗(CFD/DSMC)耦合方法[15-17],对圆锥导流结构作用下,地外天体起飞过程中起飞器受到的羽流导流气动力效应进行了研究,分析了不同上升距离以及偏转角度条件下,起飞器受到的力矩变化规律,并对起飞过程中可能出现的现象及原因进行了分析。
1 仿真模型
仿真模型如图1所示,主体分为起飞器和起飞平台。起飞器底部包含4个半球形机构、弧形底板和一个主发动机,主发动机轴心通过起飞器几何中心且与起飞器轴心重合,如图2所示。该发动机为双组元发动机,推进剂为一甲基肼(MMH)/四氧化二氮(NTO)。起飞平台包括一个圆锥导流结构和平面。
上升距离D定义为发动机出口距离起飞平面的高度,偏转角度θ定义为以起飞器质心为中心,沿着Ypc负方向进行偏转的角度。当发生偏转时,半球形机构4靠近起飞平台,半球形机构2远离起飞平台。如图2所示。
本文主要针对不同上升距离D和偏转角度θ条件下起飞器受到的羽流导流气动力效应进行数值模拟研究,具体工况位置如表1所示,其中D=200 mm,θ=3°和5°工况并未进行计算,因为D=200 mm 为起飞初始距离时,偏转角度 θ不会过大。
2 仿真方法
CFD/DSMC耦合方法已经成熟地应用于羽流的研究中,在羽流的连续流区选用CFD方法进行仿真,在稀薄流区采用DSMC方法进行仿真研究。本文利用这一方法对地外天体起飞过程中起飞器受到的羽流导流气动力效应进行仿真研究。
2.1 CFD方法
本次研究中选用计算流体学仿真软件Fluent作为CFD方法的求解器,对连续流区进行仿真计算。Fluent采用基于密度的求解器,并选用SST k-ω模型计算湍流黏性系数,通量格式采用二阶精度的Roe平均通量差分法(ROE-FDS),时间推进采用下上三角矩阵对称Gauss-Seidel方法(LUSGS)。
连续流边界条件如图3所示,计算目的是为稀薄流区DSMC提供参数条件,考虑到羽流流场下游不会影响上游,因此进行连续流计算的模型中并未建立起飞器模型。在连续流计算过程中,所有偏转角度θ=0°工况均采用二维轴对称计算模型,所有偏转角度θ不为0°的工况均采用三维计算模型。发动机入口设为压强入口,总压为0.8 MPa,总温为3040 K。发动机壁面设置为无滑移绝热壁面,导流机构壁面为恒温壁面(300 K)。
为了同时保证计算精度和计算效率,对网格的质量进行了评价,图4为3种不同网格结果对比,其中黑色对应200万网格,红色对应350万网格,蓝色对应500万网格。从图中可以看出,200万网格计算结果与350万网格的确存在一定差异,约为3.4%,而350万网格与500万网格计算结果无明显差异,约为0.1%。结合计算能力,选取350万网格即可得到满意的网格质量和计算效率。
图3 CFD计算边界条件Fig.3 Computing boundary conditions of CFD
2.2 DSMC方法
求解DSMC选用的软件为北京航空航天大学自主研发的PWS软件,这一软件也已经成功应用于羽流的仿真研究中,其精度已经经过多次验证[18-19]。
DSMC计算所需入口边界条件由CFD计算所得的结果选取,为了确保入口边界有效,防止受到下游流场的干扰,入口边界根据克努曾数Kn以及马赫数Ma选取,保证Kn<0.01,Ma>1。DSMC入口边界从CFD计算结果中选取三维网格坐标、密度、压强、温度、速度、马赫数和组分摩尔分数等参数作为DSMC稀薄流计算边界条件。

图4 3种不同网格压强结果对比Fig.4 Pressure comparison of three different grid results

图5 DSMC计算边界条件Fig.5 Computing boundary conditions of DSMC
稀薄流区仿真计算域如图5所示,网格尺寸选择为当地分子自由程的1/3,每个网格中粒子数不低于15个。计算过程中选取可变硬球模型(VHS)作为二体碰撞模型,并采用纯扩散气表面相互作用模型来达到足够的表面粗糙度。所有壁面均采用恒温壁面(300 K),壁面热适应系数统一选取为1。
3 结果与分析
3.1 仿真校验
为了验证第2节所述计算方法的精度,对文献[13]在真空羽流实验系统中进行的120 N双组元发动机缩比起飞器羽流效应实验进行了仿真计算,120 N发动机燃烧室参数总压为0.8 MPa,总温为3 040 K。计算过程中,连续流区和稀薄流区的参数设置与本次计算参数一致,即连续流区发动机壁面设置为无滑移绝热壁面,导流机构壁面为恒温壁面(300 K);稀薄流区计算过程中选取VHS作为二体碰撞模型,并采用纯扩散气表面相互作用模型来达到足够的表面粗糙度。所有壁面均采用恒温壁面(300 K),壁面热适应系数统一选取为1。
利用上述方法计算得到的120 N发动机羽流效应结果与实验结果进行了对比,图6为实验中起飞器底部压强测点位置以及4条仿真对比曲线位置,图7为实验结果与仿真结果对比,其中,s为图6中各位置与中心点的平面距离,p为压强。
图7中,Line 1和Line 3曲线位于4个半球形机构位置,压强较高,仿真结果与实验结果偏差在10%左右,Line 2和Line 4曲线位于弧形底板位置,此处压强较低,仿真结果与实验结果偏差在20%左右,这一偏差主要是由实验安装误差以及发动机工作状态与理想状态的偏差导致的。

图6 4条仿真曲线与实验压强测点位置Fig.6 Four simulation curves and experimental pressure measuring point position

图7 实验与仿真结果对比Fig.7 Comparison of experimental and simulation results
3.2 连续流场仿真结果
本文利用Fluent软件对羽流连续流区进行计算,针对18个计算工况,选取部分具有代表性的算例进行流场分析。图8为Case 1(200 mm,0°)和Case 7(400 mm,0°)工况下羽流连续流区压强云图。
从对内流场的计算结果中发现,当上升距离D为200 mm时,由于导流装置与喷管出口较近,导流装置对喷管内流动产生较强的影响,发动机燃气并未完全扩张至发动机出口,而是在发动机扩张段中间位置形成正激波,随着上升距离D的增加,到达400 mm距离附近,正激波位置逐渐扩张至发动机出口。定义β为激波至发动机喉部距离与发动机扩张段长度的比值;φ为计算得到的发动机推力与额定推力的比值。β和φ与上升距离D的关系如图9所示,可以看出,随着上升距离D的增加,激波位置逐渐由发动机内部扩张至发动机外部;当激波位于发动机内时,发动机产生的推力较小,随着激波位置外移,推力逐渐增大,并在激波到达发动机出口后趋于稳定。

图8 连续流场压强云图Fig.8 Pressure contour of continuous flow field
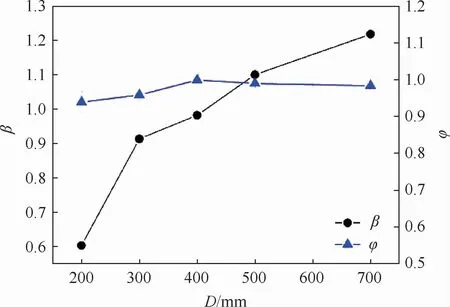
图9 β和φ随上升距离的变化Fig.9 Variation ofβandφwith rising distance
3.3 稀薄流场仿真结果
羽流稀薄流场采用北京航空航天大学自主研发的PWS软件进行计算。针对18个计算工况,选取部分具有代表性的算例进行流场分析。图10为Case 5(300 mm,3°)和Case 13(500 mm,3°)流场云图。对DSMC计算所得的稀薄流场云图进行分析可以看出,圆锥导流结构的羽流导流效果较好,但仍有少部分羽流气体返流至起飞器底面,尤其在半球形机构表面形成局部高压区域。
图11为Case 5(300mm,3°)和Case 13(500mm,3°)起飞器底面云图。从2组云图中可看出,起飞器半球形机构和弧形底板局部区域明显受到羽流返流影响。
通过对羽流流场和起飞器底部云图进行分析,可以发现当起飞器上升距离D较低,偏转角度θ较小时,靠近起飞平台的半球形机构4和弧形底板受到羽流作用明显(Case 5半球形机构4),其表面压强高于远离起飞平台一侧(Case 5半球形机构2);当上升距离D达到一定值,并偏转较大角度时,远离起飞平台一侧的半球形机构2和弧形底板受到羽流作用明显(Case 13半球形机构2),其表面压强高于靠近起飞平台一侧(Case 13半球形机构4)。
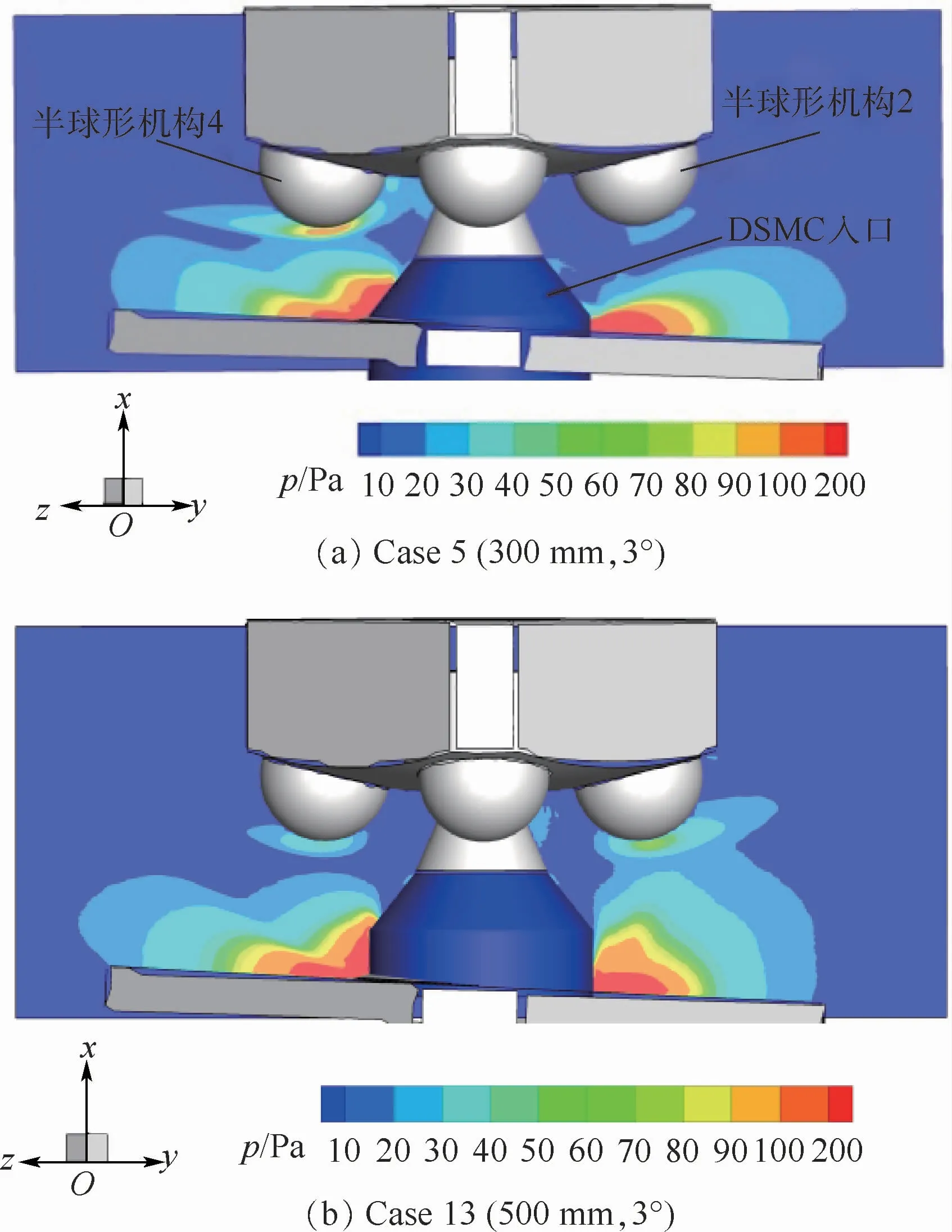
图10 稀薄流场压强云图Fig.10 Pressure contour of rarefied flow field

图11 起飞器底面压强云图Fig.11 Pressure contour of bottom of ascender
3.4 起飞器所受力矩
本次仿真起飞器受到的沿Ypc方向的力矩结果如图12所示。由于偏转方向为Ypc负向,因此在上升距离D较低,偏转角度较小时,力矩Typc为正值。从图12(a)中可以看出,在偏转角度 θ=0°时,起飞器受到的Ypc方向力矩基本为0 N·m,这主要是由于起飞器属于对称结构;在偏转角度θ=1°时,起飞器受到的Ypc力矩随着上升距离D的增加首先为正向力矩,且逐渐减小,但是当上升距离到达500 mm附近,力矩从正向转向负向力矩,并逐渐负向增加;在偏转角度 θ为3°和5°时,力矩规律与偏转角度为1°时相似,在上升距离D为450 mm左右,力矩逐渐从正向力矩转变为负向力矩,然后随着上升距离D的增加先负向增加,后负向减小。从图12(b)中可以看出,上升距离D=200~400 mm时,Ypc方向的力矩随着起飞器偏转角度θ的增加而正向增大;但是当上升距离D>500 mm时,Ypc方向的力矩随着起飞器偏转角度θ的增加而负向增加。

图12 Y pc方向力矩变化趋势Fig.12 Torque variation trend of Y pc direction
由此可见,当上升距离D和偏转角度θ逐渐增加时,起飞器受到的力矩出现反向增加现象,由纠正偏转力矩逐渐变为加剧偏转的力矩。
3.5 仿真结果分析

图13 Case 1工况下羽流密度场膨胀波和压缩波示意图Fig.13 Schematic diagram of expansion and compression waves of plume density field of Case 1
计算得到的压强极值位置反向以及力矩反向现象可以通过流场流动特点进行解释。图13为Case 1(200 mm,0°)工况下连续流区和稀薄流区的羽流密度场云图(ρ为羽流密度),从图中可以看出,由于起飞器与起飞平台结构复杂,在羽流从喷管流出直至作用于起飞器的过程中,存在较为复杂的波系。在这一复杂的波系中,促使羽流作用于起飞器表面的主要为如下2点:①由于喷管内压强较高,从而在喷管出口附近形成的膨胀波;②羽流作用于圆锥导流结构后产生的压缩波。当羽流经过上述膨胀波和压缩波后,速度大小和方向均会发生改变,如图14所示。
图14中,v为速度,l为羽流与起飞平台作用位置距离起飞平台轴线的距离,L为圆锥导流结构底部半径,α为羽流与起飞平台作用后压缩波与导流机构表面形成的偏转角度。图15为Case 15(700 mm,0°)工况下马赫云图,从图中可以看出羽流与着陆器表面作用位置即膨胀波与起飞平面作用位置,因此l选取方式较为明确,而压缩波为曲面,α选取为羽流作用点与压缩波曲面切线角度。

图14 经过压缩波和膨胀波后的羽流速度变化Fig.14 Variation of plume velocity after expansion and compression waves

图15 Case 15工况下l与α选取示意图Fig.15 Schematic diagram of l andαselection under working condition of Case 15
在地外天体起飞的过程中,随着起飞器上升距离D和偏转角度θ的改变,l与α均随之改变。偏转过程中,靠近起飞器一侧羽流与起飞平面作用位置始终在圆锥导流结构上,导流效果较好。力矩反向等现象主要受到远离起飞器一侧羽流流动变化影响。图16给出了远离起飞器一侧羽流与起飞平台作用点相对位置变化规律,其中l/L为作用点位置与圆锥半径的比值,当l/L=1时,代表圆锥半径位置。从图16中可以看出,随着上升距离D和偏转角度θ的增加,远离起飞器一侧的羽流作用点逐渐脱离锥面进入平面内。
图17给出了远离起飞器一侧压缩波角度α变化规律,可以看出:D≤300 mm时,α随着偏转角度θ增加而减小;当D =400~500 mm时,α随着偏转角度θ增加先减小后急剧增加,最后趋于平缓,这主要是由于随着θ的增加,羽流作用点位置逐渐由圆锥导流结构移动至平面附近;当D=700 mm附近,α随着偏转角度 θ增加逐渐增大,当θ达到3°后逐渐降低,这主要是由于700 mm时,羽流作用点在1°时已经位于圆锥边缘位置附近,并且随着θ增加逐渐远离圆锥。

图16 远离起飞器一侧羽流作用点相对位置变化规律Fig.16 Variation of relative position of plume impact point on the side far away from ascender
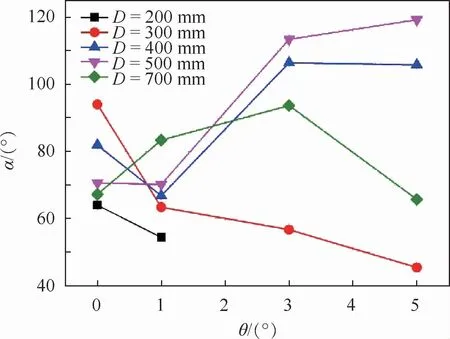
图17 远离起飞器一侧压缩波角度α变化规律Fig.17 Variation of compression wave angleα on the side far away from ascender
通过上述分析可以发现,上升距离D的增加和偏转角度θ的增加都将导致发动机羽流与导流机构的作用点发生改变,尤其在距离起飞器较远距离一侧,作用点在较大距离和角度下可能由圆锥表面移动至平面,导致压缩波角度α出现较大幅度增加,根据图14所示羽流速度变化与角度α的关系,可以看出α较大时,羽流更容易返流至起飞器底面,从而形成压强极值位置反向以及力矩反向等现象。
4 结 论
本文利用CFD/DSMC耦合的方法,对圆锥导流结构作用下,地外天体起飞过程中起飞器受到的羽流导流气动力效应进行了研究。分析了不同的上升距离和偏转角度情况下,起飞器可能受到的羽流导流气动力影响,得到如下结论:
1)当上升距离较低时,发动机燃气会在喷管扩张段中部形成正激波,无法完全扩散至喷管出口,发动机推力较小,随着上升距离的增加,激波位置逐渐移至发动机喷管出口外,推力增加并趋于稳定。
2)起飞器底部受到羽流返流影响较严重区域随着上升距离和偏转角度的增加逐渐从靠近起飞平台一侧变为远离起飞平台一侧。
3)随着上升距离和偏转角度的增加,起飞器受到的羽流导流气动力矩发生方向的转变,如在负向偏转角度下,由最初的正向力矩逐渐转变为负向力矩。
4)通过对羽流流场中压缩波和膨胀波的位置变化及其对羽流流动影响进行分析,发现力矩反向等现象产生的原因为发动机羽流与起飞平台的作用点从圆锥导流结构表面移动至平面,从而使起飞平台表面压缩波角度增加,羽流作用于起飞平台后的流动方向由贴近起飞平台向侧面流动急剧转变为反弹至起飞器底面方向流动。
研究结果指出了地外天体起飞过程中圆锥导流结构可能引起的羽流效应影响,为后续的研究及设计工作提供有效的参考。根据仿真结果,建议在起飞过程中,利用额外姿控发动将起飞器姿态控制在偏角较小范围内。
