进动弹道目标平动补偿与分离

韩立珣，田波，冯存前，2，*，贺思三

（1.空军工程大学 防空反导学院，西安710051； 2.信息感知技术协同创新中心，西安710077）

弹道导弹中段防御一直是国际政治和军事领域关注的重点。弹道目标识别是一种典型的非合作式目标识别，目标的形状、结构、表面材料电磁参数和常规运动特性等特征对先验信息要求较高，而攻击方弹道导弹参数通常很难获取，这些特征在弹道导弹目标识别中的实用性受到限制，而且弹道目标通常会在中段释放子弹头诱饵，此时传统的目标识别方式难以从中分辨出真弹头，而基于难以模仿的目标固有属性微动特性的应用为其提供了新的突破口[1-3]。

目前，国内外在弹道目标微动特性方面已经做了大量的研究，其中，文献[4]得出多点和噪声对微多普勒提取影响不大这一结论。文献[5]提出可以将中段弹道目标的平动近似为多项式表达，利用最小二乘法估计出了平动参数，但该方法只适用于单散射源或目标含有一个强散射源和若干个弱散射源的情况。文献[6]利用形态学中的骨架提取方法得到了清晰的微多普勒曲线。文献[7]利用Viterbi算法构造时频滤波器从而提取出时频图中各个信号分量，但该方法只能用于时频曲线交叠不明显的情况，不具备普遍适用性。

本文针对以上问题，提出了一种利用图像处理领域中的角点检测进行平动补偿的方法，可以对含有多散射点的目标实现较好效果的平动补偿。然后利用基于交点信息的分段Viterbi算法对回波信号实现了分离处理，较好地解决了传统Viterbi算法的频率跳变及错误关联问题。

1 进动锥体弹道目标微动特性

锥体弹道目标的进动模型如图1所示。以弹头的进动轴为z轴，弹头质心为坐标原点O，进动轴与弹头自旋轴为yOz平面，x轴满足右手螺旋定理。设弹头质心O距弹头顶端A的距离为h1，距弹头底部圆心的距离为h2，弹头总高度设为h，弹头底面圆的半径为r，半锥角为ε。弹头进动轴与自旋轴夹角为θ，初始时刻的方位角为φ0，进动角速度为ωc，自旋角速度为ωs。雷达视线（LOS）入射方向的俯仰角α，方位角为φ，与自旋轴的夹角为 β。

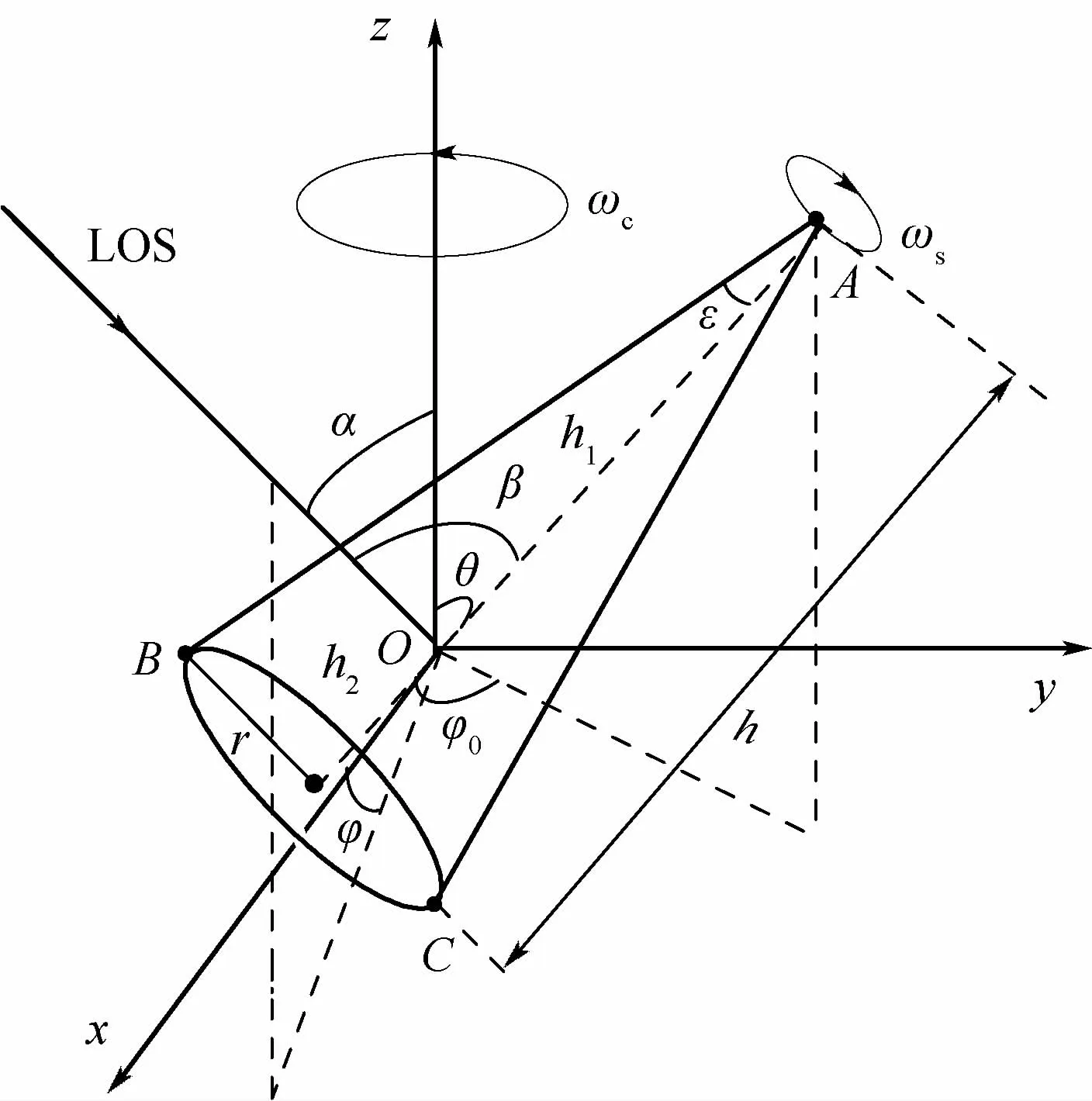
图1 锥体弹道目标进动模型Fig.1 Cone ballistic target's precession model

理论计算和测量试验均表明，锥体弹道目标的散射中心通常表现为入射线和目标对称轴所构成的平面与目标不连续处边缘的交点[8]。由此可知，当雷达波束照射到处于进动状态的锥体弹道目标时，会在锥顶A，锥底边缘与电磁波入射平面的交点B、C处形成散射中心。

在不考虑遮挡效应的情况下，文献[8]分别对3个散射点进行分析，可以得到在t时刻各个散射点的微多普勒公式分别为

式中：F（t）=sinθsinαsin（ωct+φ0）+cosθcosα，λ为信号波长；ω为角速速。

可以看出，对于理想散射点A，该点的运动仅仅表现为自旋，运动方式较为简单，符合正弦调制规律；对于滑动散射点B、C，这两点的运动表现为自旋和锥旋的合成，运动形式比较复杂，不再满足简单的正弦调制规律。

此时假设雷达发射波长为λ的信号，则接收到的雷达基频回波信号可以表示为

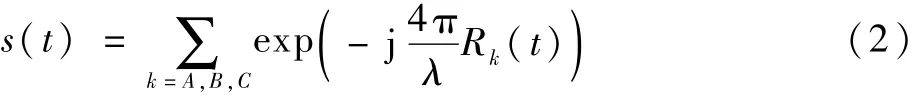
式中：Rk（t）为t时刻k散射点与雷达的径向距离。

物体处于高速平动时会出现多普勒折叠现象，弹道目标在中段飞行时，弹道是相对平稳的，此时雷达会处于“粗跟”状态。可以利用某个观测时间内的脉冲测得的速度vi对回波信号进行重构补偿，从而完成对速度的粗补偿[9]。粗补偿后的径向距离可以近似表示为

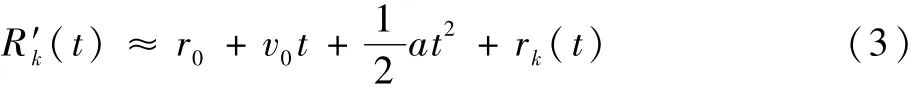
式中：r0、v0、a和rk（t）分别为t时刻散射点k的径向初始距离、速度、加速度和微动距离。

在实际雷达回波中要考虑遮挡效应带来的影响，通过分析可以得出各个散射点的可见条件如表1所示。

表1 散射点可见角度Table 1 Visible angle of scattering points

可以设一个条件函数 γ（t），当满足表1时，γ（t）的函数值为1，其余时刻为0。

综上所述，基频回波信号可以表示为

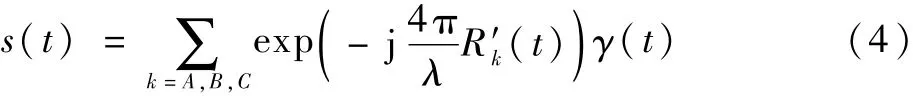
基频信号相位的一阶导数即为频率信息，因此可以推导出进动锥体弹道目标的频率为

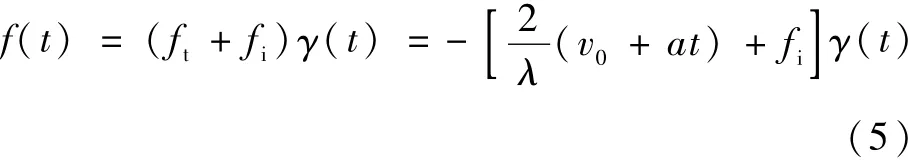
式中：ft和fi分别为目标平动与微动导致的频率。

2 基于角点检测的平动补偿

通过式（1）和式（5）可以看出，当各个散射点的频率相同时（表现为时频图上的曲线交点），应当满足fi=0这一条件，即时频图上曲线的交点所对应的频率与目标散射点的微动特性无关，完全受平动控制，所以可以通过交点信息反推平动信息，从而进行精度较高的平动补偿。

在这里引进图像处理领域中的角点检测[10]算法提取时频图的交点信息。

现有的角点检测算法一般分为3类[11]：基于结构边缘轮廓的角点检测[12]；基于图像灰度强度的角点检测[13]；基于模板匹配的角点检测。常见的角点检测算法有Harris算法、Harris-Laplace算法、He&Yung[14]算法等。其中基于Harris算法的角点检测方法被公认为是效果较好的角点检测方法之一。但Harris算法存在对尺度变换敏感且提取出的角点是像素级别的缺陷，Harris-Laplace算法存在极值、定位精度以及冗余检测等问题。如将上述方法直接运用到时频图的交点检测中，检测的效果不是很理想。

可以分别在以下2个方面加以改进。

1）对时频图进行预处理。采用数学形态学图像处理技术对时频图进行加工。通过这一处理可以较好地消除噪声的影响、提高分析精度。

2）采用改进的Harris角点检测方法。针对Harris角点检测方法的不足，采用一种基于双边滤波器的Harris角点检测方法。具体流程如下：

从而建立双边滤波函数w（x，y）为

式中：u为归一化常数；σk和 σh分别为空间距离标准差和灰度距离标准差。

步骤2 利用双边滤波函数得到自相关函数矩阵M。

步骤3 计算角点检测算子R。

式中：det M 表示M 矩阵的行列式；tr M 表示矩阵M 的迹；q为一常数，这里取0.06。当R值为像素点在3×3范围内最大值且大于设定的阀值时即可认为该点为角点。

在检测出角点后，提取出角点的坐标（x，y），数值x即为时频图交点的时间点取值，数值y即为时频图交点的频率取值。原则上只需2个交点信息即可求解出平动项参数v0、a的信息，在这里为保证精度减少误差，可以将交点两两组合求解出一组平动项参数信息再取平均即可估计出平动参数。

在利用时频图交点求解出平动参数即v′0、a′后，即可利用平动补偿函数s′（t）对原来的回波进行平动补偿。

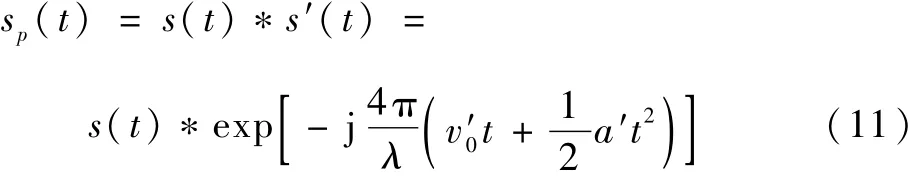
3 基于交点信息的曲线分离

Viterbi算法[15]是一种以信号能量大小为依据，对多分量信号进行抽取的算法。这种算法假设瞬时频率曲线是一条相对平滑的曲线，对瞬时频率估计就是为了使下式的估计路径最小化：

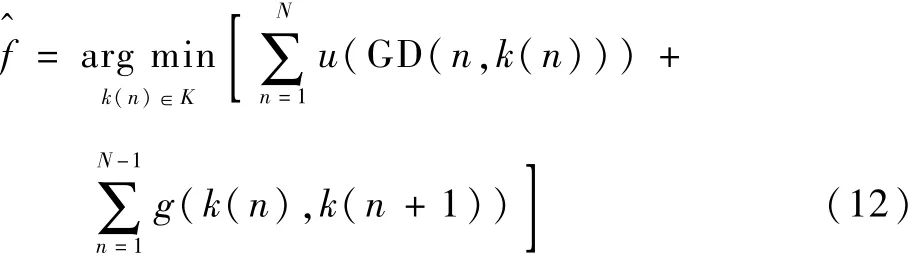
式中：K为时频分布中所有可能路径的集合；N为采样点个数；u（x）为定义在GD（n，k（n））函数上的代 价 函 数，表 征 点 的 权 值；g（x，y）表 示的代价函数，在这里依据下式取值：

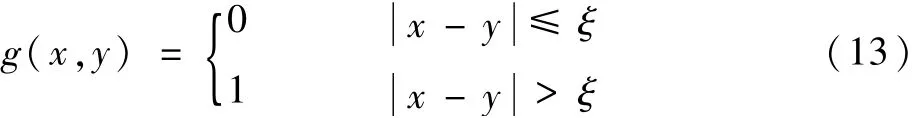
式中：ξ为相邻2个瞬时频率点频率变化的期望值，一般取决于时频变换的频率分辨率[16]。

在经过平动补偿后，时频曲线将会聚焦在零频附近，此时如果采用传统的Viterbi算法进行曲线分离，将会在时频曲线交点处产生错误关联从而无法精确分离各个曲线[17]，而且往往会因为交点处的复杂情况导致计算时间大大增加。在这里提出一种可以充分利用之前所提取出交点信息的分段Viterbi算法对交叉程度较高的弹道目标回波时频图进行分离，具体步骤如下：

步骤1 根据交点信息将曲线分段。

步骤2 利用Viterbi算法对每段图像分别进行曲线分离。

步骤3 分别计算每段图像交点附近不同曲线的斜率，利用斜率大小对曲线进行编号。

步骤4 将相邻两段图像编号相同的曲线合并，从而实现整体曲线的分离。

4 仿真实验

进行以下仿真实验验证本文算法的有效性。

仿真参数设置：设雷达发射载频为6 GHz，脉冲重复频率为500 Hz，带宽为5 MHz的单频信号，观测时间为2 s，信噪比为2 d B。锥体弹道目标的锥体高度h1=2 m、h2=0.5 m，底面半径r=0.5 m，进动角 θ=10°，进动角速度 ωc=4πrad/s，雷达视线入射方向的俯仰角α=，与自旋轴的夹角β=。经过平动预补偿后的v=-2 m/s、a=2.5 m/s2。

图2仿真了在经过平动预补偿后，锥体弹道目标的3个散射中心造成的回波多普勒曲线，可以看出在观测时间内3条曲线共有8个共同的交点，且3条曲线随时间作同方向的近似线性倾斜运动。

随后对图2中的时频曲线进行加工。建立一个25×25像素的高斯空间掩模对图像进行平滑处理，再进一步将其转化为二值化图像，然后提取图像骨架得到图3。

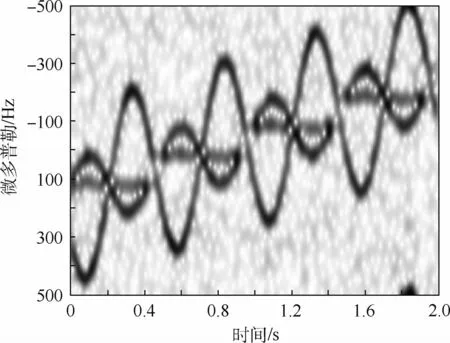
图2 锥体弹道目标回波时频图Fig.2 Time-frequency image of cone ballistic target echo

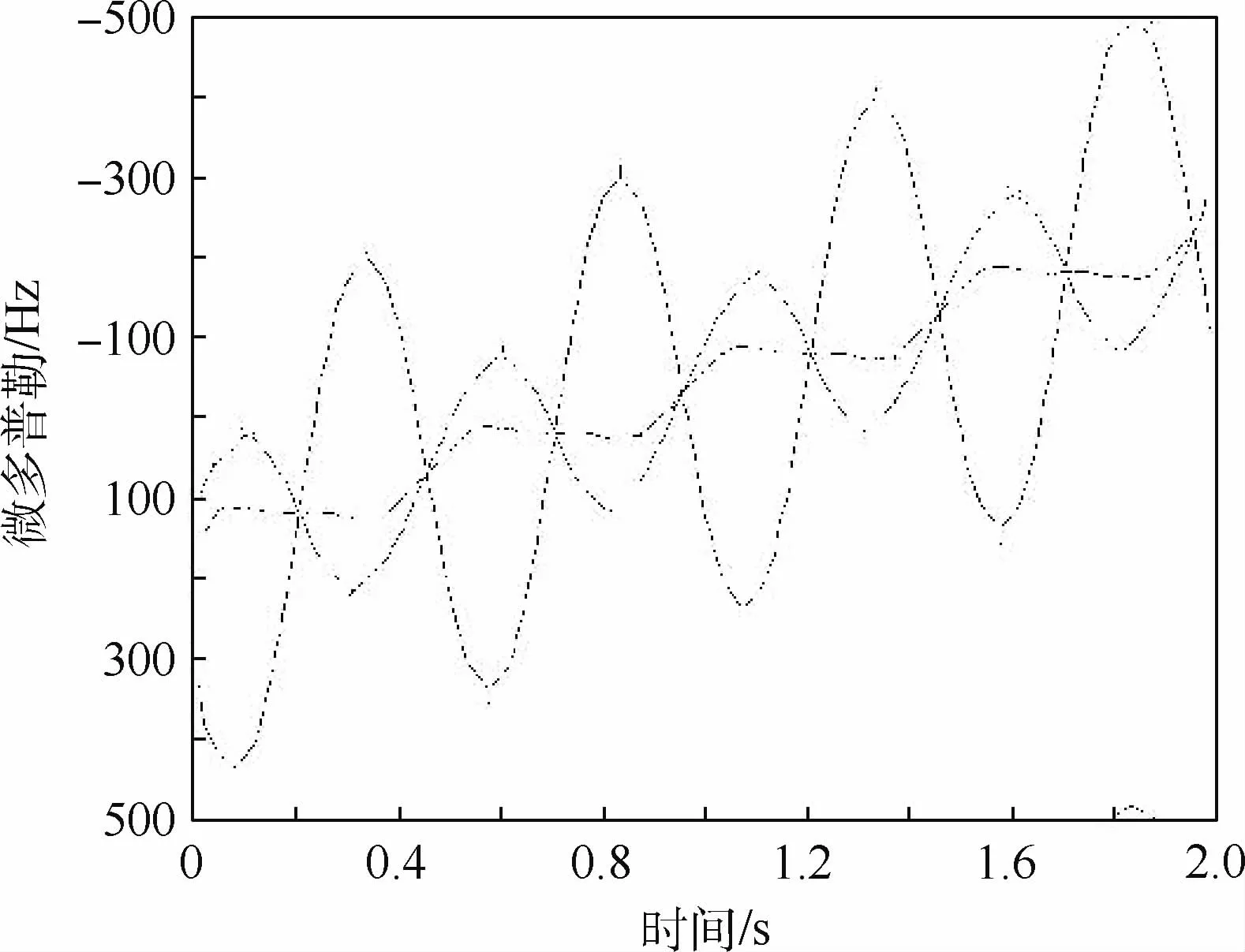
图3 时频曲线骨架Fig.3 Time-frequency curve skeleton

对于图3可以采用本文提及的角点检测算法得到角点坐标。因角点检测算法是对整个图像进行检测，图像的坐标轴和单位等部分被当成检验对象后，会出现大量位于坐标轴上的多余角点并增加检验时间，从而影响整体检测的结果，故这里在角点检测前先将图像的坐标隐去，只对所需要的时频曲线进行检测。

综上，分析两罪犯罪构成要件的不同之处，我们很容易将二者区分，并清晰探知嫖宿幼女罪在刑法分则中所处位置的意义，它与强奸罪有重合部分，但又各司其职，属于特别法与一般法的关系。

将检测到的角点绘制在图4中。可以看出此时检测出12个角点，其中第2、5、6、7个曲线交点处有多个角点聚集，第3个曲线交点未检测出角点。由这12个曲线交点坐标估计出平动参数v=-1.958 8 m/s，a=2.460 5 m/s2。

利用估计出的平动参数结合式（11）对回波信号时频图进行平动补偿可以得到图5。从图5中可以看出，平动补偿很好地消除了平动项对时频图的影响，此时时频曲线近似分布在零频附近，从而验证了本文算法的有效性。

再在图5的基础上对时频曲线进行加工并提取出角点，可以得到图6。从图6中可以看出，总共检测出9个角点，这9个角点其中的8个是曲线的交点，有一个是曲线的最高点。利用这9个交点坐标对图5进行分段处理，将时频曲线分为9段可以得到图7。再利用本文提出的分段Viterbi算法对每段图像进行处理，对每一段的时频曲线进行分离，结果如图8所示。

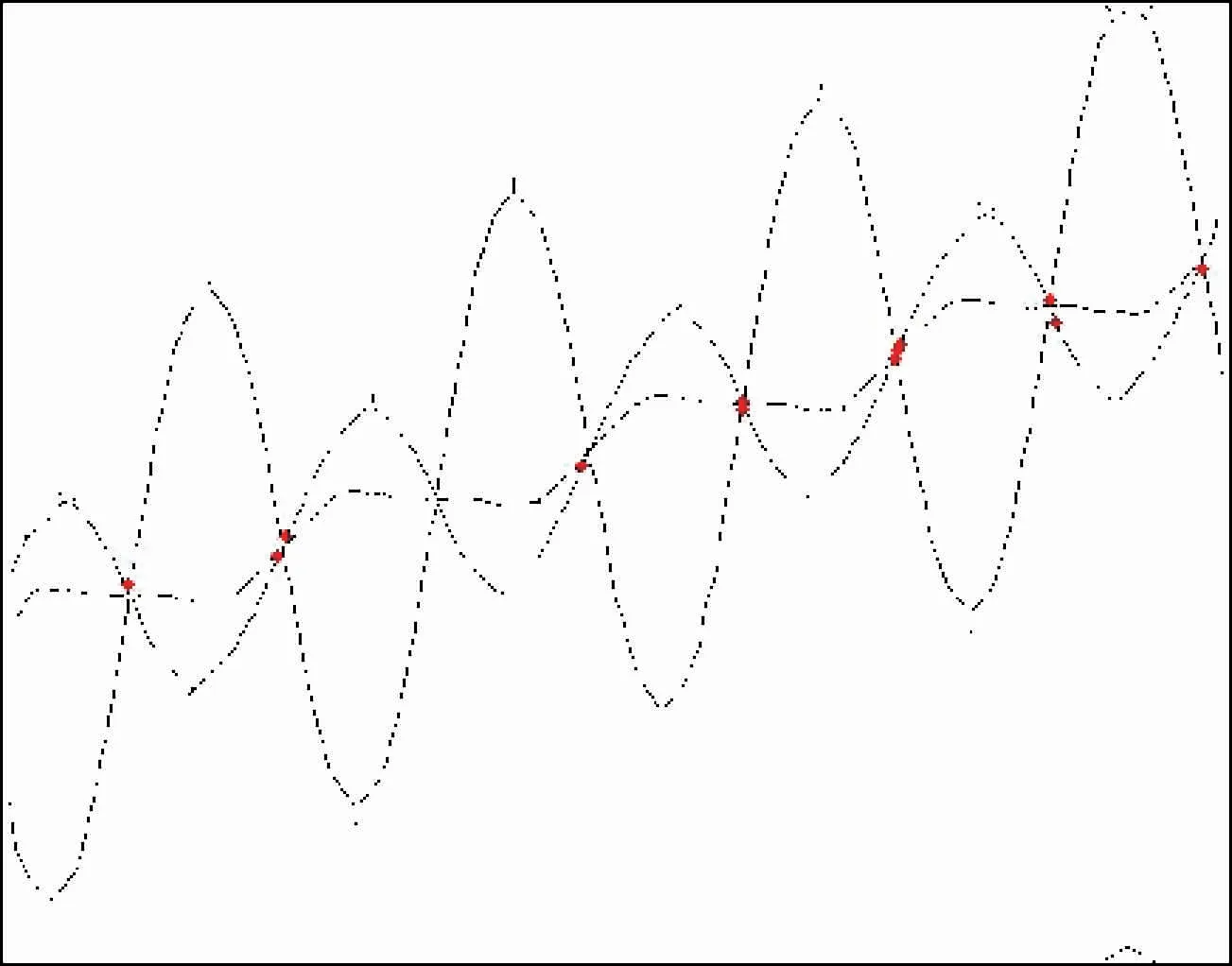
图4 角点检测图Fig.4 Corner detection image

图5 平动补偿后的时频图Fig.5 Time-frequency image after translation compensation

图6 平动补偿后的角点检测图Fig.6 Corner detection image after translation compensation

将相邻两段图像斜率相同的曲线用相同颜色标识，然后将相同颜色的曲线合并即可得到完整的分离曲线，如图9所示。

图10为采用文献[7]中的Viterbi算法直接对时频图中曲线进行分离的结果。

从图9、图10的对比中可以看出，本文提出的分段Viterbi算法较传统的Viterbi算法在交点处分离曲线的准确度有很大提升。原因是本文提出的分段Viterbi算法利用时频曲线中的交点对图像进行处理，充分利用了图像本身的特性，将复杂的处理过程简洁化，从而避免了Viterbi算法带来的频率跳变及错误关联问题。

为进一步分析本文提出算法在不同信噪比情况下的分离效果，接下来在不同信噪比条件下各进行100次的蒙特卡罗仿真，定义归一化均方根误差为

图7 分段处理效果图Fig.7 Periods processing effect image

图8 分段Viterbi算法分离处理Fig.8 Separation processing by segmentation Viterbi algorithm

图9 分段Viterbi算法抽取的曲线Fig.9 Curves extracted by segmentation Viterbi algorithm

图10 Viterbi算法抽取的曲线Fig.10 Curves extracted by Viterbi algorithm

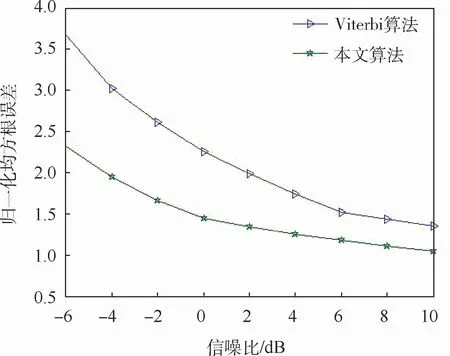
图11 本文算法与Viterbi算法对比Fig.11 Comparison between proposed algorithm and Viterbi algorithm

随着信噪比的增加，归一化均方根误差整体呈下降趋势，且在信噪比大于6 d B后，曲线趋于平稳，这是由于骨架提取的固有缺陷造成的。从图中可以明显看出，本文所提算法的归一化均方根误差要小于Viterbi算法。

5 结 论

本文通过分析进动锥体弹道目标微动特性，提出了一种利用时频曲线交点信息进行平动补偿与曲线分离的方法。

1）弹道目标的时频图是多个散射点微动分量叠加的结果，想要直接进行平动补偿往往很困难。利用交点处微多普勒与散射点微动特性完全受平动效应支配这一结论，本文先采用改进的Harris角点检测方法提取出时频曲线交点坐标，再根据交点进行平动补偿，仿真实验表明该方法具有良好的平动补偿效果。

2）针对传统Viterbi算法在交点处出现的频率跳变及错误关联现象，本文充分利用交点信息，先对时频图进行分段处理，再利用Viterbi算法对每一段时频图进行分离处理，最后再进行曲线合并得到完整的分离曲线。仿真实验表明该理念的正确性。

3）对算法进行了蒙特卡罗仿真实验，仿真结果表明在不同信噪比情况下本文算法的归一化均方根误差均小于Viterbi算法，具有良好的抗噪性与较高的准确度。

4）在仿真中发现，由于骨架提取的固有缺陷，通过本文算法分离出的曲线与原始数据始终有一定的误差，如何减少这一误差，提高曲线分离准确度将是下一步研究的重点。