混合式惯导系统姿态四元数连续自标定模型

王琪，汪立新，周小刚，沈强

（火箭军工程大学 导弹工程学院，西安710025）

混合式惯导系统是一种新型惯导系统，其吸收了平台式和捷联式惯导系统的各自优点，并且将隔离载体角运动的物理平台、捷联姿态算法与旋转调制抑制误差效应这三者集于一体。该系统主要着眼于高速和高动态运载器对高精度惯导提出的新需求，不仅能大幅度提高导航定位精度，实现快速精确自对准，还可实现装机条件下的自标定以及明显降低购置和维护成本[1]。

惯性系统误差标定补偿是提高系统精度的有效手段，针对混合式惯导系统三轴全姿态物理平台和系统装机自标定的特点，选择运用连续自标定方法进行混合式惯导系统的误差自标定。连续自标定是Jackson[2]于1973年提出的一种动态标定方法。其基本原理如下：惯性平台在外力矩的作用下以角速度ωc（称为加矩角速度）转动，在地球自转角速度、加矩角速度以及重力加速度的激励下，加速度计输出中包含有陀螺仪误差、加速度计误差、安装误差和平台对准误差等全部误差信息。以加速度计输出为观测量，以平台对准误差方程为动力学模型，采用最优滤波算法估计平台误差系数和对准误差，并用估计结果对平台模型进行补偿与调整[3]。相比于传统的多位置自标定，连续自标定中惯性平台转动的每一个采样点都相当于多位置自标定中的一个位置，因此连续自标定方法能够以比多位置自标定更高的精度同时标定出惯性平台的全部误差系数。

传统的连续自标定针对平台式惯导系统，主要有基于失准角和基于框架角的2种自标定模型。文献[4]系统地介绍了平台连续自标定的失准角模型、可观测性分析、参数辨识等内容。文献[5-6]针对大失准角情况下传统的失准角误差模型会产生较大误差的问题，建立了框架角误差模型。文献[7-8]分析了平台连续自标定中各误差系数的可观测性，并针对安装误差可观测性低这一问题，分别建立了以加速度计输入轴和陀螺仪输入轴为基准的平台坐标系，减少了安装误差项，使所有的安装误差变得可观，提高了标定精度。

考虑到混合式惯导系统采用捷联姿态算法，而捷联姿态算法中使用姿态四元数来描述物体转动，四元数表示能够避免传统的欧拉角表示中大量的三角运算带来的舍入误差，从而提高计算速度和标定精度[9]。以四元数为基础的四元数卡尔曼滤波（Quaternion Kalman Filter，QKF）在惯性导航系统的姿态估计[10]和自对准[11]问题都已有一定应用。因此本文在混合式惯导系统框架角约束方程的基础上，利用姿态四元数代替欧拉角描述混合式惯导系统中三轴物理平台的转动，建立一种混合式惯导系统姿态四元数连续自标定模型，并且针对这一模型的特点，提出了一种基于奇异值分解的四元数无迹卡尔曼滤波（Unscented Kalman Filter based on Singular Value Decomposition Quaternion，SVD-QUKF）来标定混合式惯导系统误差系数。通过仿真和试验比较了基于姿态四元数模型的SVD-QUKF算法和基于框架角模型的UKF算法的标定结果，证明本文提出的自标定模型和标定算法在计算速度和标定精度上较传统方法都有一定优势。

1 惯性平台姿态四元数与框架角之间的转换关系

首先给出混合式惯导系统中的坐标系定义，混合式惯导系统采用隔离载体角运动的三轴物理平台，物理平台通过3个框架轴固联在基座上，其中惯性平台固联在台体轴上，台体轴固联在内环轴，内环轴固联在外环轴，外环轴固联在基座上，由此构成具有三自由度的稳定平台。三轴物理平台由3个陀螺仪与3个加速度计组成，如图1所示。定义如下坐标系：

1）框架坐标系（K）：XK、YK、ZK三轴分别指向混合式惯导系统的外框架轴、内框架轴、台体轴，三者构成右手正交坐标系。

2）平台坐标系（p）：以加速度计敏感轴为基准定义，取三轴物理平台几何中心为原点，Xp轴与X加速度计敏感轴平行，Yp轴平行于X和Y加速度计敏感轴所确定的平面，并与Xp轴垂直，Zp轴与Xp轴以及Yp轴构成右手正交坐标系。

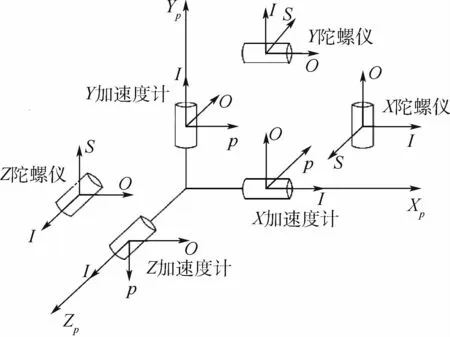
图1 三轴物理平台组成Fig.1 Three-axis physical platform geometry

根据惯性平台台体和3个框架轴之间的固联关系可知，无论3个框架轴如何转动，都可以通过绕ZK—YK—XK轴的顺序使平台台体转回原位置，对于p系来说，就是绕Yp—Xp—Zp轴的顺序转回原位置。若假设惯性平台绕XK、YK和ZK轴转动角度分别为 θx、θy和 θz，则对于p系来说，就是依次绕Zp、Xp和Yp轴分别转动 θx、θy和 θz。根据四元数定义，描述惯性平台转动的姿态四元数为

同时，姿态四元数到框架角的转换关系为

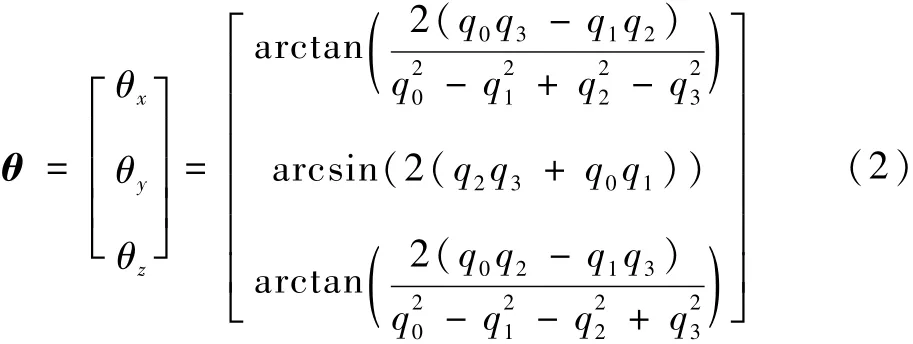
2 混合式惯导系统连续自标定模型

2.1 混合式惯导系统框架角约束方程

混合式惯导系统在地面标定时处于稳定和稳定加旋转2种工作模式[1]，此时混合式惯导系统的工作原理与平台式惯导系统相同，因此可以采用平台式惯导系统的框架角约束方程。利用框架角约束方程建立自标定模型能够避免失准角模型中的小角度假设，从而能够适用于大失准角的情况。假设惯性平台绕XK、YK和ZK框架轴转动的框架角分别为 θx、θy和 θz，则其框架角约束方程为[6]

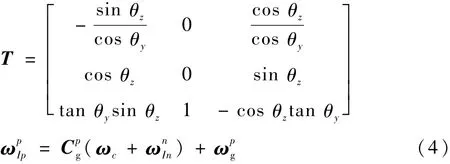
In=[0 ωIEcos L ωIEsin L]T，ωIE为地球自转角速度值，L为当地纬度；ωpg为平台漂移，由陀螺仪误差引起的，混合式惯导系统所用的光纤陀螺仪具有很好的线性度，二次项误差基本可以忽略不计[12]，只需要考虑其零偏误差和随机误差，所以有

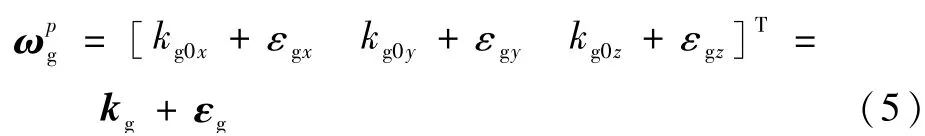
式中：kg0i（i=x，y，z）为陀螺仪零次项误差系数；εgi为陀螺仪量测噪声。

2.2 加速度计输出方程

加速度计的输出与加速度计三轴敏感的比力有关，加速度计三轴上的比力为

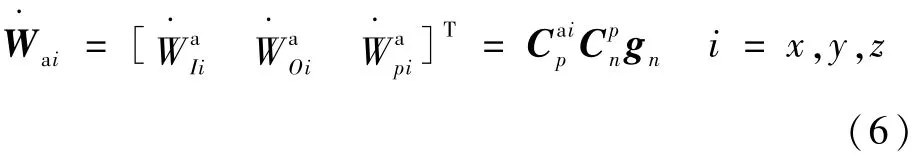
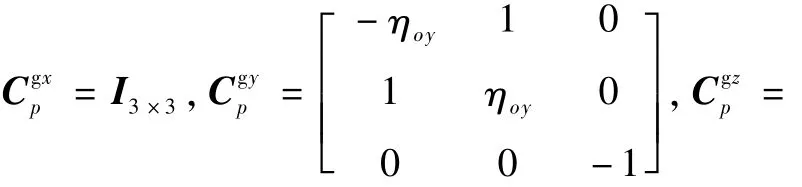
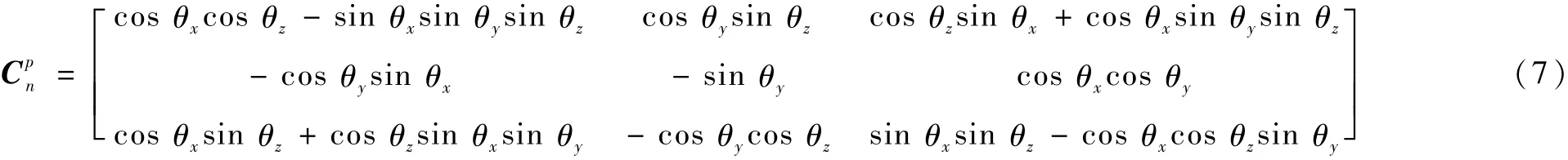
则加速度计输出方程为[13]

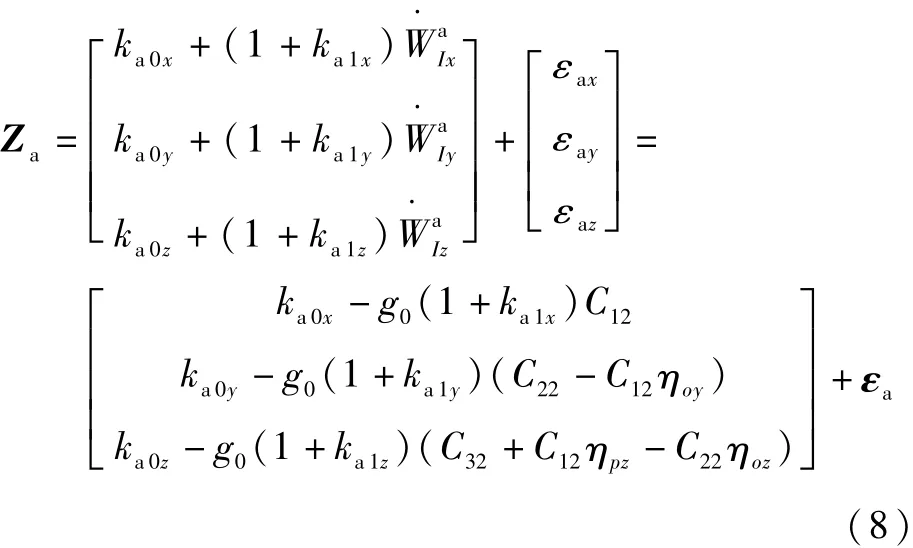
式中：kaji（j=0，1；i=x，y，z）为加速度计误差系数；εa为加速度计量测噪声；Cmn（m，n=1，2，3）为矩阵Cpn的元素。

以框架角约束方程为系统方程，以加速度计输出和框架角传感器输出为系统量测，结合式（3）～式（5）和式（8），则可以得到基于框架角的连续自标定模型（以下简称为框架角模型）为

2.3 四元数连续自标定模型

对式（1）进行求导，整理可得四元数微分与框架角微分之间的关系为

式中：Tq为矩阵T的四元数表示。

考虑框架角传感器的量测噪声，将 θi+vi（i=x，y，z）代入式（1）可得带有噪声干扰的四元数为

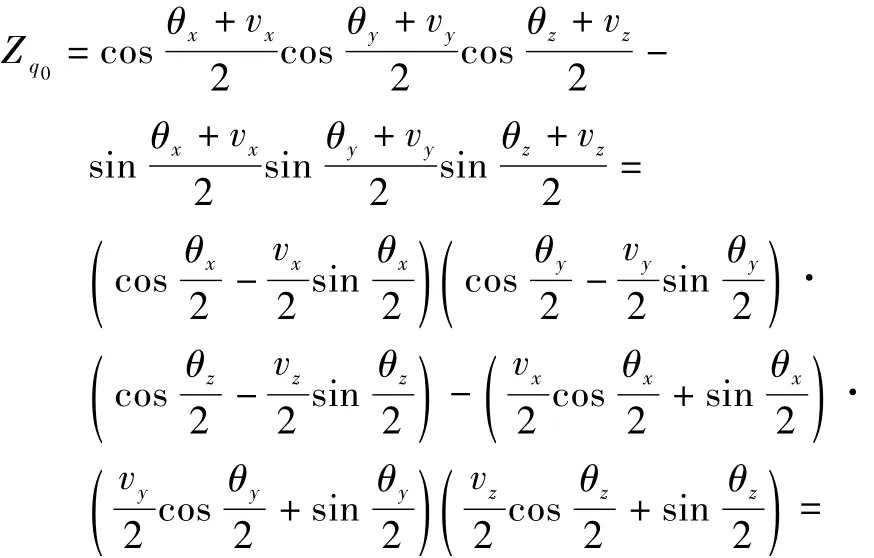
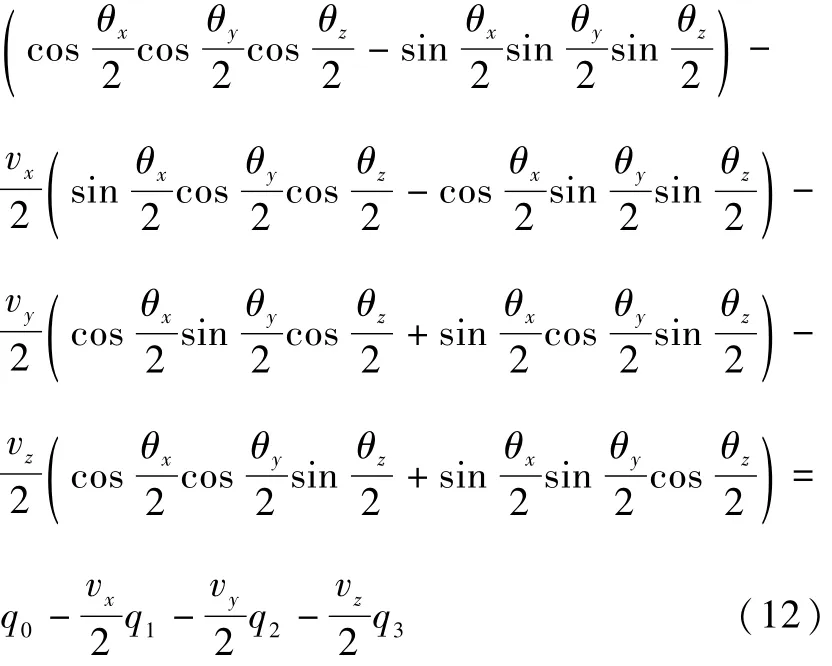
同理可得

因此，包含噪声的姿态四元数量测方程为

式中：

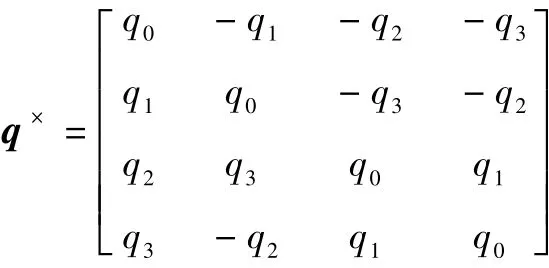
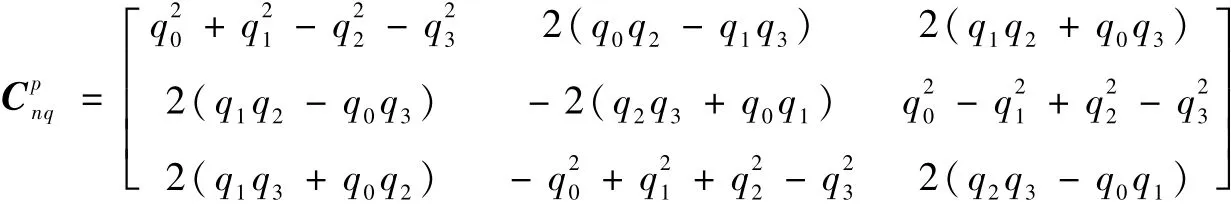
同时用Cpnq代替式（8）中的Cpn，则式（9）中的观测方程可以写为

结合式（11）和式（15），可得混合式惯导系统的四元数连续自标定模型（以下简称为四元数模型）为

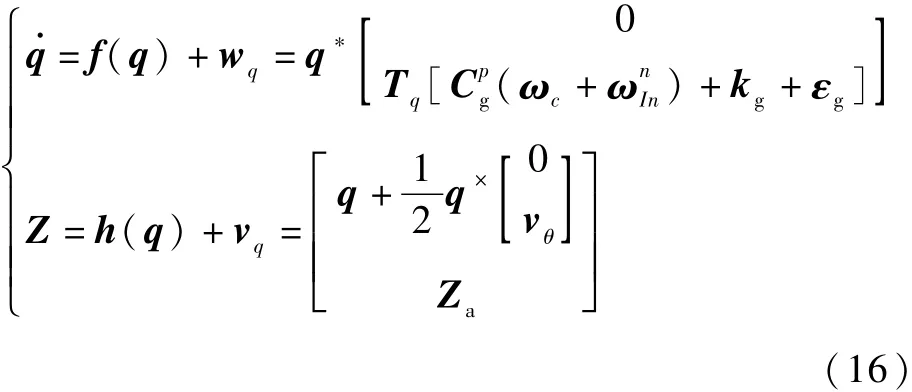
混合式惯导系统采用捷联姿态算法，而捷联姿态算法中使用姿态四元数来描述物体转动，四元数模型正好满足这一要求。同时，四元数表示能够避免传统的欧拉角表示中大量的三角运算带来的舍入误差，提高计算速度和标定精度，并且四元数表示不存在奇异点，因此能够避免惯性平台连续转动过程中可能出现的“框架自锁”现象。

3 基于奇异值分解的四元数无迹卡尔曼滤波

可以看出，式（16）的四元数模型是一个强非线性的系统方程，因此选择UKF对其进行状态估计和参数辨识。但是有2个问题需要解决：①在UKF滤波过程中，由于量测噪声、截断误差和状态模型扰动等因素的影响，状态协方差矩阵P容易变得非正定，然而在UKF中利用Cholesky分解获取σ样本点时，要求P必须正定；②在将欧拉角表示转换为四元数表示之后，原来3维的系统噪声和量测噪声都变成了4维噪声，系统噪声方差阵Q和量测噪声方差阵R的形式也随之发生变化，需要重新进行推导。

3.1 奇异值分解

针对第一个问题，本文选择奇异值分解代替Cholesky分解来获取σ样本点。因为奇异值分解不要求被分解矩阵为正定，同时，如果被分解矩阵是正定的，那么奇异值分解和Cholesky分解的结果是相同的[14]。奇异值分解的结果为

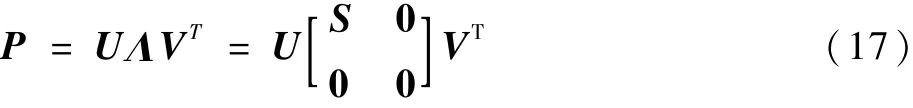
式中：P∈Rm×n，m≥n；Λ∈Rm×n；U∈Rm×m；V∈Rn×n；S=diag（s1，s2，…，sr），s1≥s2≥…≥sr≥0为矩阵P的r个奇异值，r=rank（P）。

3.2 系统噪声方差阵和量测噪声方差阵的推导

根据系统噪声方差阵Q和量测噪声方差阵R的定义，有Q=E[wwT]和R=E[vvT]。根据2.3节中的推导可知，在将欧拉角表示转换为四元数表示之后，系统噪声和量测噪声变为wq=，则四元数表示的系统噪声方差阵Qq和量测噪声方差阵Rq的表达式有如下推导：

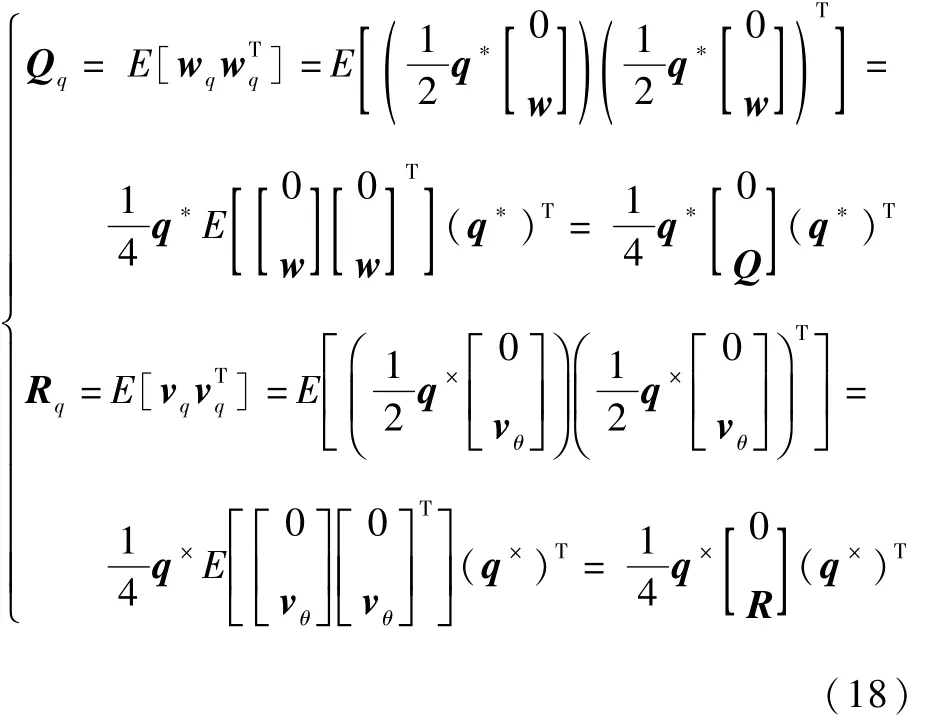
式中：Qq，Rq∈R4×4。

3.3 SVD-QUKF算法步骤

在将欧拉角表示转换为四元数表示之后，系统噪声wq和量测噪声vq由加性噪声变为了非加性噪声，此时需要将其扩展为系统状态量[15]。此外，待标定的惯导系统误差系数也扩展为系统状态量，则扩展后的系统状态量为

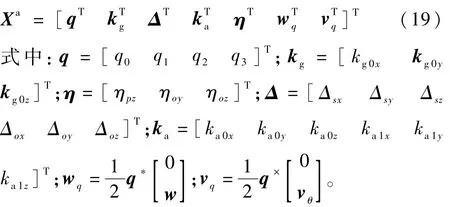
状态协方差矩阵P为

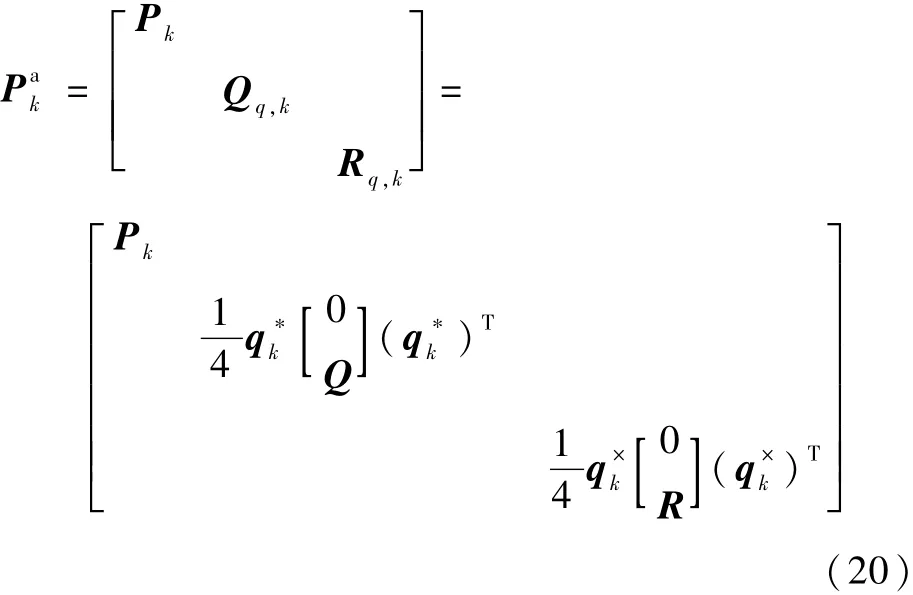
对式（16）进行离散化，则可得到SVD-QUKF的滤波方程为

式中：ΔT=0.2 s为离散时间间隔。

则SVD-QUKF的算法步骤如下：

1）滤波初值

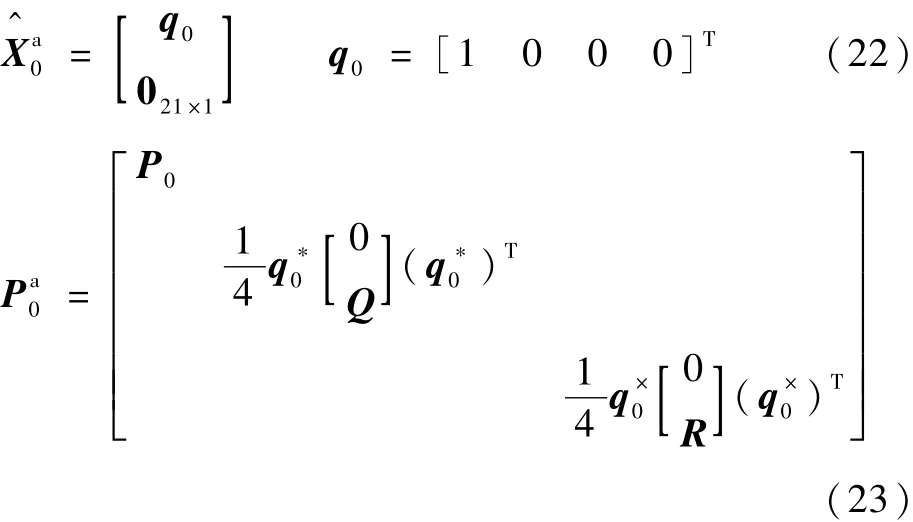
2）计算σ样本点

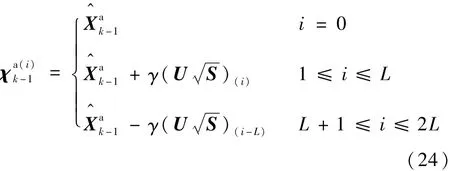
式中：U和S为式（17）中状态协方差矩阵P的SVD分解结果

3）时间更新

4）量测更新

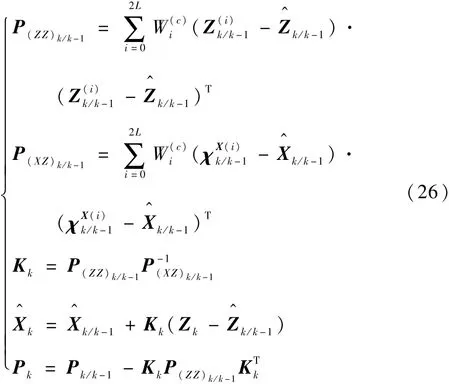
5）归一化

在每一次迭代之后，都需要对姿态四元数进行归一化以保证其为标准四元数[16]，即

4 仿真和试验

4.1 仿真分析

为验证本文提出的四元数模型的适用性，运用SVD-QUKF算法对式（16）的四元数模型进行了参数辨识，运用UKF算法对式（9）的框架角模型进行了参数辨识，对二者结果进行对比。混合式惯导系统三轴物理平台的转动路径如下[17]：

1）起始角度为 θx=0°，θz=0°，以 角 速 度1（°）/s绕ZK轴转动 π。

2）起始角度为 θx=0°，θz=π，以角速度1（°）/s绕XK轴转动 π/2。

3）起始角度为 θx=π/2，θz=π，以角速度1（°）/s绕ZK轴转动 π。

4）起始角度为 θx=π/2，θz=0°，以角速度1（°）/s绕XK轴转动 π/2。

定义系统状态量的估计误差和相对估计误差以表示标定精度：

式中：Δx为估计误差；e为相对估计误差；x^和x分别为系统状态量的估计值和真值。

首先，为了比较2种系统模型对框架角的估计精度，将框架角模型估计得到的框架角转换为四元数与四元数模型估计得到的四元数进行了对比，估计误差如图2所示。

从图2可以看出，四元数模型对于框架角的估计误差小于框架角模型，所以对于框架角的估计精度，本文提出的四元数模型要优于传统框架角模型。

其次，为比较2种模型对于混合式惯导系统误差系数的标定精度，表1给出了所有误差系数在2种系统模型下的相对估计误差和算法计算时间，图3给出了部分误差系数的相对估计误差曲线。

从表1可以看出，使用SVD-QUKF的四元数模型的计算时间远少于使用UKF算法的框架角模型，这是因为SVD-QUKF算法中采用的四元数表示避免了欧拉角表示中大量的三角运算，从而减少了计算时间。在实际的惯导系统自标定中，是采用实时滤波的方法进行误差系数辨识，根据仿真时间可得，原始算法进行一个卡尔曼滤波周期需要13 ms，这已经比较接近于一般惯导系统20 ms的计算周期，不利于进行实时滤波，而本文的算法进行一个卡尔曼滤波周期所需时间为7 ms，能够保证实时性要求。同时可以看出，在相同的转动路径和仿真条件下，四元数模型对于混合式惯导系统误差系数的估计精度也要优于传统的框架角模型，特别是对于陀螺仪和加速度计的安装误差系数的标定精度提高较大。仿真结果表明，相比于传统的框架角模型，本文提出的四元数模型能够有效提高混合式惯导系统的误差系数标定精度。

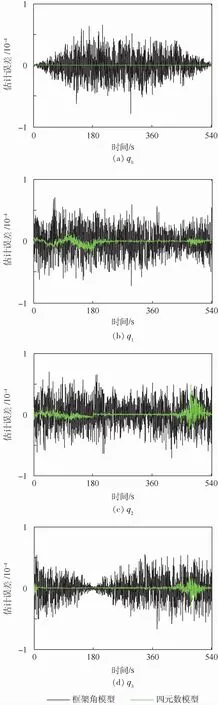
图2 四元数模型和框架角模型的框架角估计误差曲线Fig.2 Estimate error curves of gimbal angle in quaternion model and gimbal angle model

4.2 试验验证

在某型平台式惯导系统上进行了试验验证。

表1 误差系数相对估计误差和算法计算时间Table 1 Computing time and relative estimate er rors of error coefficients

由于硬件限制，试验中只各绕ZK轴和XK轴进行了一次转动：

1）起始角度为 θx=0°，θz=0°，以 角 速 度1（°）/s绕ZK轴转动 π。

2）起始角度为 θx=0°，θz=π，以角速度1（°）/s绕XK轴转动 π。

采集加速度计和框架角传感器的输出，利用传统的框架角模型和本文提出的四元数模型进行了误差系数标定，对于框架角的估计误差如图4所示，其均方根误差（RMSE）如表2所示。从图4和表2可以看出，四元数模型对于框架角的估计精度要高于框架角模型，从而验证了其适用性。同时可以注意到，在图4中，在绕ZK轴转动完毕和刚开始绕XK轴转动时，估计误差会发生较大的波动，这是因为当加速度计接近水平位置时，加速度计输出中噪声比很大，从而会造成滤波结果偏离真值，甚至有可能导致滤波结果发散，这种情况是需要避免的。具体做法是：在设置自标定程序时，根据框架角传感器的输出判断加速度计是否接近水平位置，当加速度计接近水平位置时，断开加速度计的输出采集回路，同时停止滤波，待加速度计离开水平位置一定角度后，再重新采集加速度计输出，继续进行滤波。

图3 k a0i（i=x，y，z）和 ηji（j=p，o；i=y，z）的相对估计误差曲线Fig.3 Relative estimate error curves of k a0i（i=x，y，z）andηji（j=p，o；i=y，z）

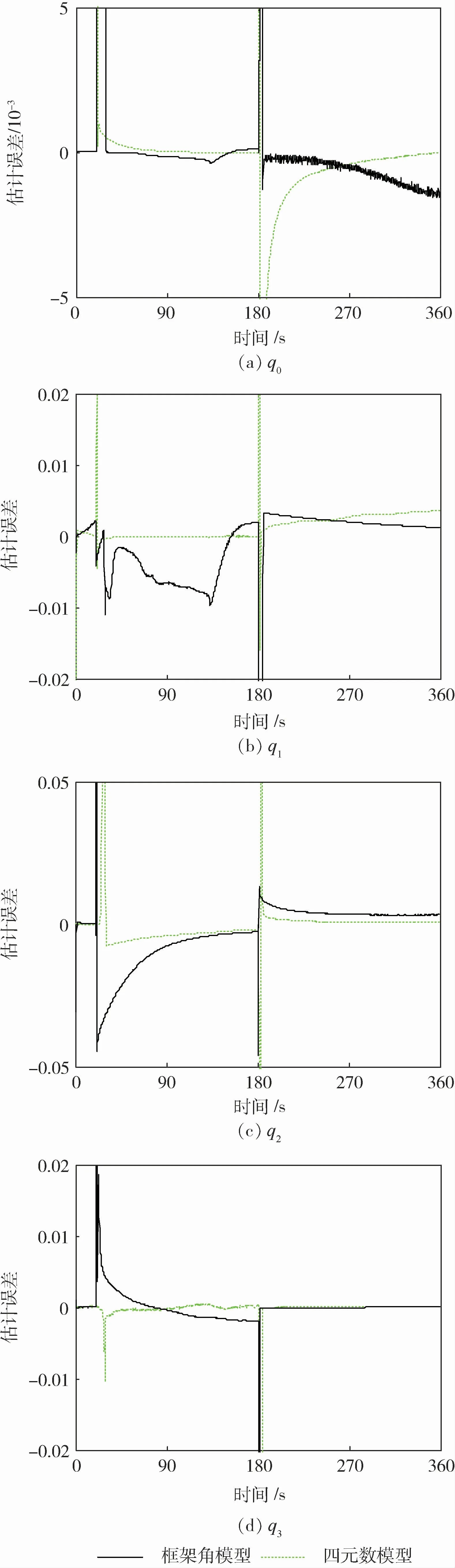
图4 试验中四元数模型和框架角模型的框架角估计误差曲线Fig.4 Gimbal angle estimate errors of quaternion model and gimbal angle model in experiment

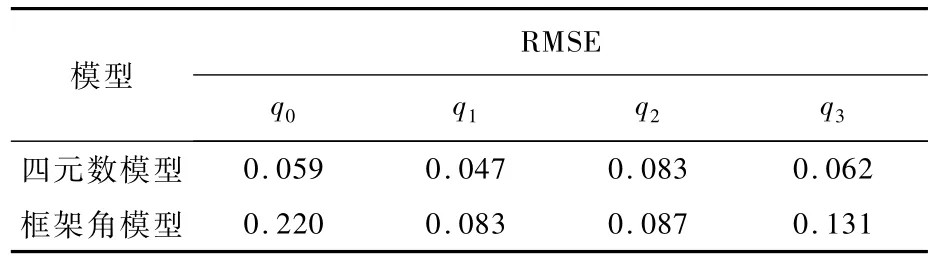
表2 四元数模型和框架角模型的框架角均方根误差Table 2 RMSE of gimbal angle of quaternion model and gimbal angle model

5 结 论

1）针对混合式惯导系统全姿态物理平台、捷联姿态算法和系统装机自标定的特点，本文在混合式惯导系统框架角约束方程的基础上，利用姿态四元数代替欧拉角描述混合式惯导系统中三轴物理平台的转动，建立一种姿态四元数连续自标定模型。

2）针对四元数连续自标定模型的特点，对传统的UKF算法进行改进，利用SVD 代替传统UKF算法中的Cholesky分解来获取σ样本点，避免了状态协方差矩阵P不正定时Cholesky分解结果奇异的现象；同时推导了四元数表示下的系统噪声方差阵Qq和量测噪声方差阵Rq，将3维噪声转换为了4维噪声，提出了一种SVD-QUKF算法用于标定混合式惯导系统误差系数。

3）仿真和试验结果表明，相比于基于传统UKF算法的框架角连续自标定模型，本文提出的四元数连续自标定模型和SVD-QUKF算法能够以低于1%的相对误差标定出混合式惯导系统所有的误差系数，在标定精度和计算速度上都有一定优势，具有实用价值。