基于快速自适应超螺旋算法的制导律
2019-07-31刘畅杨锁昌汪连栋张宽桥
刘畅,杨锁昌,*,汪连栋,张宽桥
(1.陆军工程大学石家庄校区 导弹工程系,石家庄050000; 2.电子信息系统复杂电磁环境效应国家重点实验室,洛阳471003)
随着现代战场的日益复杂,传统比例导引已经远远不能满足制导系统的发展需求。人们将先进的控制理论应用于导弹的制导系统中,如最优控制、逆系统控制、H∞控制、微分几何控制、随机系统最优控制、滑模变结构控制等,以解决强对抗条件下的精确制导问题。最优制导律虽然在理论上可以实现零脱靶量,但形式复杂,需要信息多,且对信息误差相当敏感。逆系统控制、H∞控制、微分几何控制、随机系统最优控制等方法虽然具有一定的鲁棒性,但均存在形式复杂、需要信息多的缺点。
滑模变结构以其抗干扰特性和设计简单而成功的应用于导弹制导律设计,但受到滑模控制固有的抖振和渐进稳定特性影响,滑模变结构制导律普遍存在抖振严重、收敛速度慢等局限[1]。克服抖振的方法之一是以饱和函数或边界层代替符号函数,但这使得系统轨迹稳定在滑模面附近而不是滑模面上,进而丧失了滑模控制的鲁棒性[2]。另一种抑制抖振的方法是采取高阶滑模控制,高阶滑模在抑制抖振的同时还能保持对干扰的鲁棒性,消除了相对阶的限制,提高了控制精度[3]。
二阶滑模是目前应用最为广泛的高阶滑模控制方法,因为它的控制器结构简单且需要信息少。螺旋算法、超螺旋(Super-Twisting,ST)算法、次优算法和给定收敛律算法是二阶滑模中常用的4种算法[4],与其他二阶滑模算法相比,ST算法仅需要滑模变量而不需要滑模变量的一阶导数,因此广泛应用于制导律设计。ST算法的有限时间稳定条件需要已知系统不确定性上界,实际应用中这个界的精确值很难确定,为得到系统的稳定控制,往往选取尽可能大的参数,结果带来系统损坏和剧烈抖振[5]。为此多种自适应ST算法相继被提出[6-8],但这些算法大多假设系统不确定性满足一定形式的假设,且在系统状态距离平衡点较远时收敛速度较慢。
针对上述问题,本文在标准ST算法的基础上引入线性项[9],设计了一种新的自适应律,提出了一种新的快速自适应超螺旋(Fast Adaptive Super-Twisting,FAST)算法,该算法不需要已知系统不确定性的边界且收敛速度较快。首先,利用类二次型Lyapunov函数[10-12]证明了系统的有限时间稳定性,并给出了收敛时间公式。随后,将FAST算法应用于末制导问题,提出了一种新的二阶滑模制导律。最后,通过数字仿真将所提制导律与自适应滑模制导律、ST制导律和光滑二阶滑模制导律进行了对比。仿真结果表明,本文算法具有更高的命中精度、更快的收敛速度和更强的鲁棒性。
1 问题描述和相关引理
1.1 问题描述
为了研究导弹拦截目标过程中的制导律,首先建立导弹与目标的相对运动模型。对于非滚转导弹,在末制导过程中,姿态控制系统可以控制导弹不滚转,因而弹目相对运动可以解耦成纵向平面和横向平面的运动。以纵向平面为例,弹目相对运动如图1所示,横向平面的推导与之类似。
图1中,M和T分别代表导弹和目标所处位置;r为平面内两者的相对距离;q为弹目视线角;vm和vt分别为导弹和目标的速度;θm和 θt分别为弹道倾角和目标航向角;am和at分别为导弹和目标的法向加速度。由图1可以得出弹目相对运动方程为[13]

为便于推导,令导弹与目标的相对径向速度Vr=相对法向速度Vq=˙,将其代入式(1)和式(2)后,对式(1)和式(2)相对于时间求一阶导数,得
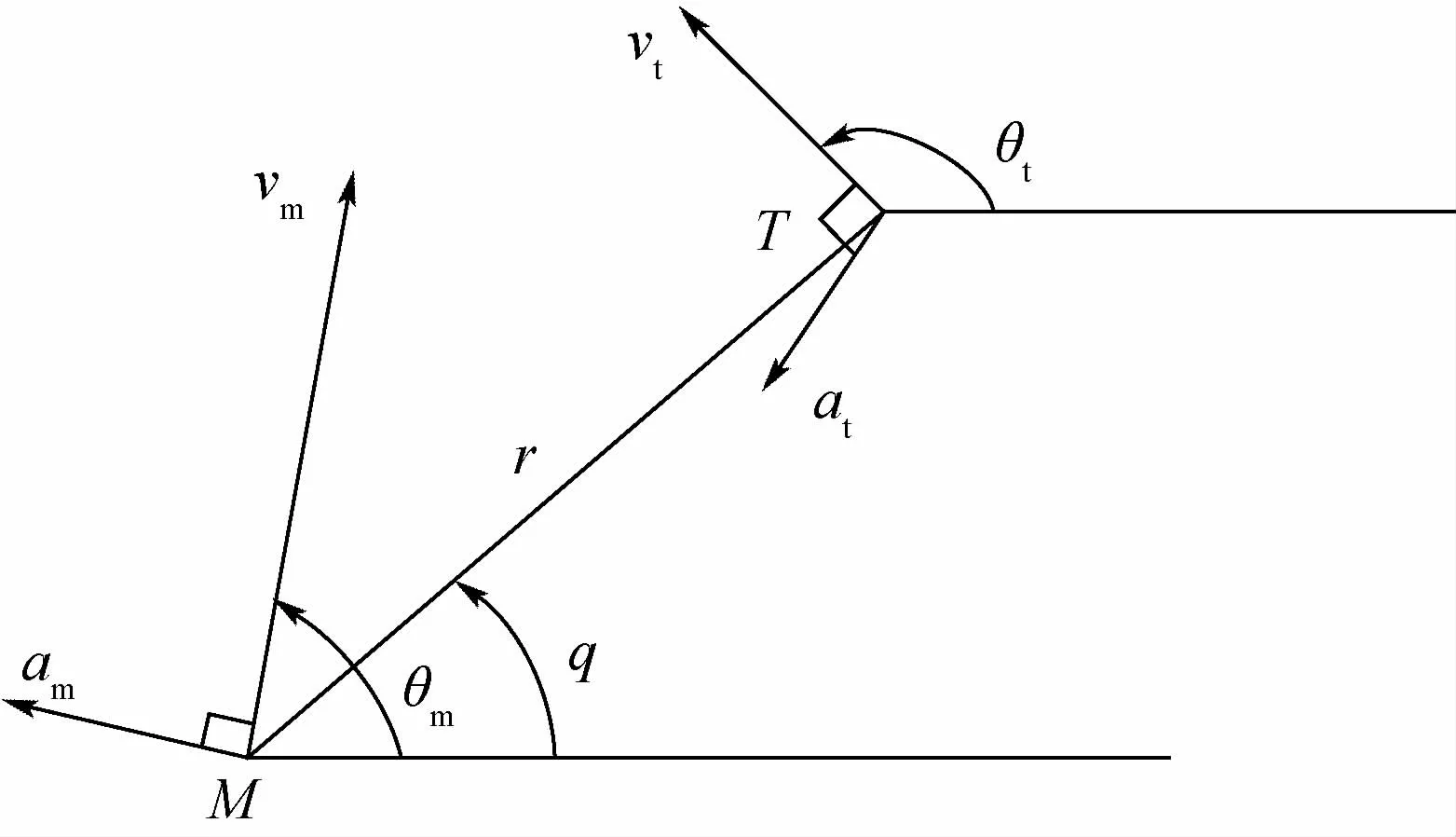
图1 导弹和目标相对运动示意图Fig.1 Schematic diagram of relative motion of missile and target

令

其中:atr和amr分别为目标加速度和导弹加速度在视线方向上的分量;atq和amq分别为目标加速度和导弹加速度在视线法向方向上的分量。
整理式(1)~式(5),得
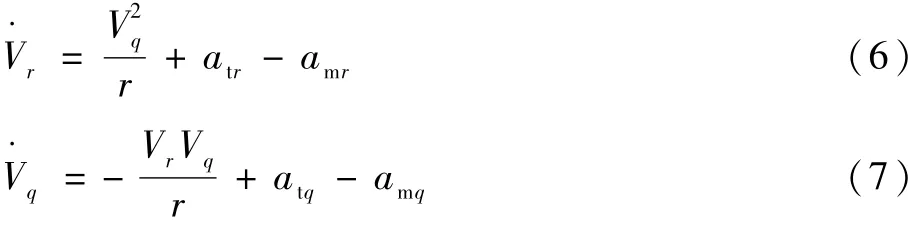
将Vr=和Vq=代入式(7),得到系统方程:
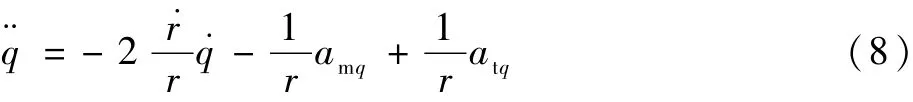
在制导律设计时,将amq和atq分别视为系统的控制量和干扰量。根据准平行接近原理,设计制导律的关键在于如何通过amq控制视线角速率˙,令其趋近于0。由式(5)可知:

在末制导过程中,由于受到过载能力的限制,导弹和目标实际所能提供的最大侧向加速度是有限的。同时受到导引头角跟踪系统的功率、接收机过载等因素的限制,导引头存在最小作用距离r0,当弹目相对距离小于或等于r0时,制导回路断开。记末制导开始时刻为0,不失一般性制导过程满足如下假设。
假设1 存在常数Am>0,At>0,A1>0,A2>0,使得

假设2 系统(8)中的时变参数r(t)满足:

1.2 相关引理
引理1[14]对于非线性系统,有

假设存在连续可微函数V(x):U→R满足:
1)V(x)为正定函数。
2)存在正实数 ζ1>0和 α∈(0,1),以及包含原点的开邻域U0⊂U,使得下式成立:
则系统(12)有限时间稳定;若U=U0=Rn,则系统(12)全局有限时间稳定。收敛时间treach满足:
引理2[15]对于非线性系统(12),假设存在连续可微函数V(x):U→R满足:
1)V(x)为正定函数。
2)存在正实数 ζ1>0,ζ2>0和 α∈(0,1),以及包含原点的开邻域U0⊂U,使得下式成立:
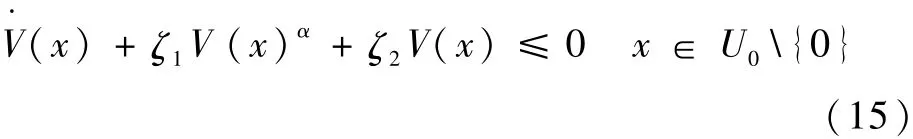
则系统(12)有限时间稳定;若U=U0=Rn,则系统(12)全局有限时间稳定。收敛时间treach满足:

2 FAST算法设计及稳定性证明
2.1 ST算法
考虑一阶系统:

式中:x∈R 为系统状态(同时也是滑模变量);u∈R和E∈R分别为控制输入和不确定项。定义E=E1(x,t)+E2(x,t),E1(x,t)表示不可微的不确定性,E2(x,t)表示可微的不确定性。
系统(17)的ST算法可表示为[16]

式中:sgn(x)为符号函数;k1和k2为待设计的参数。若和k2的取值满足[4]:显然,k1和k2需要根据不确定性的上界确定。
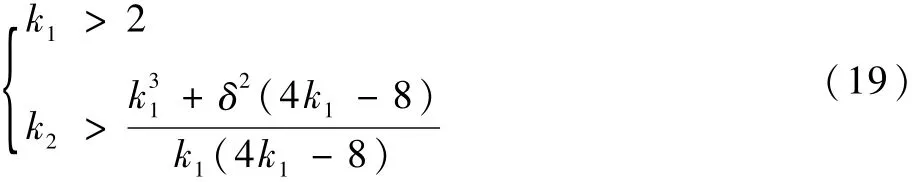
将式(18)代入式(17),令x1=x,x2=u1,化简后的控制系统为

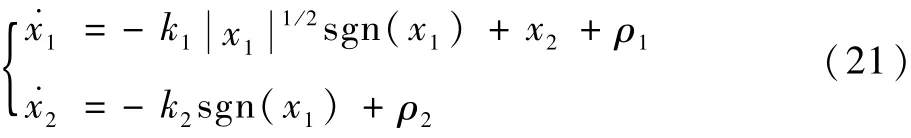
式(21)的有限时间稳定性证明及收敛时间估计见文献[4]。
2.2 FAST算法设计
假设3 E1(x,t)和E2(x,t)满足:

式中:g1和g2为未知正数;φ1(x)和 φ2(x)为滑模变量的函数,对不同的控制律有不同的形式。
针对系统(17),设计FAST算法如下:

式中:
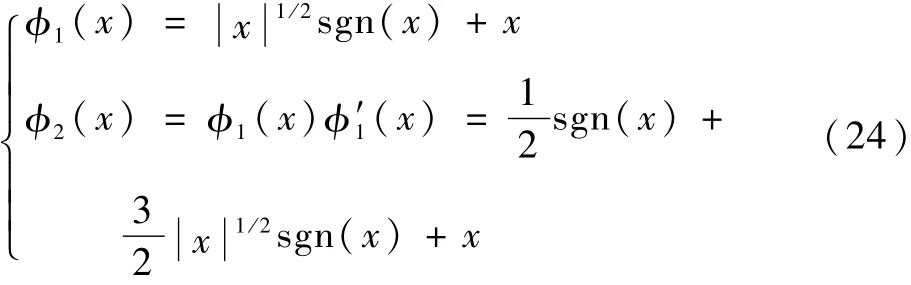
自适应参数控制器为
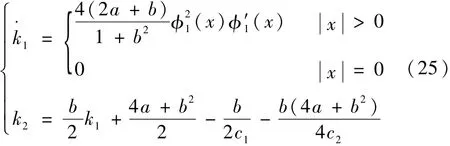
式中:a、b、c1和c2为任意正数。
将式(23)代入式(17),得到控制系统为
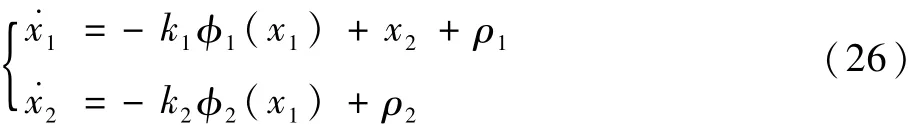
式中:
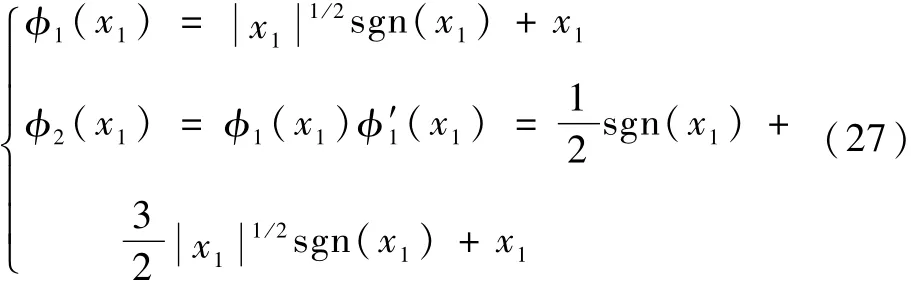
自适应参数控制器为

2.3 有限时间稳定性证明
令ξT=[φ1(x1),x2],由

可得

式中:

由假设3可知:
式(31)的等效形式为
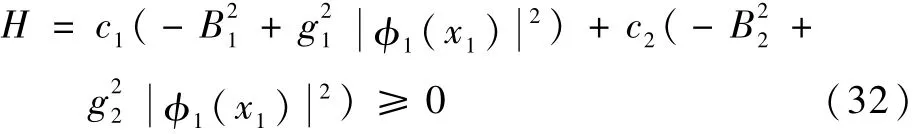
式(32)可改写为
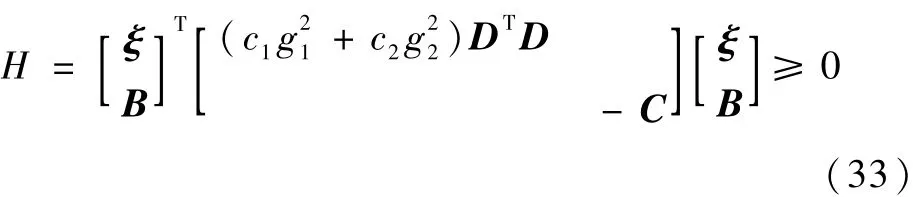
定理1 当系统(26)满足假设3时,存在k1*和k2*使得x1和x˙1在有限时间treach内从任意初始位置收敛到0。
证明
令

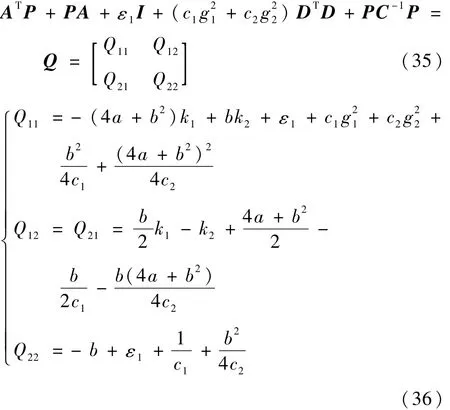
式中:ε1为足够小的正常数。若

则Q11<0,Q22<0,Q12=Q21=0,于是Q为半负定矩阵。令
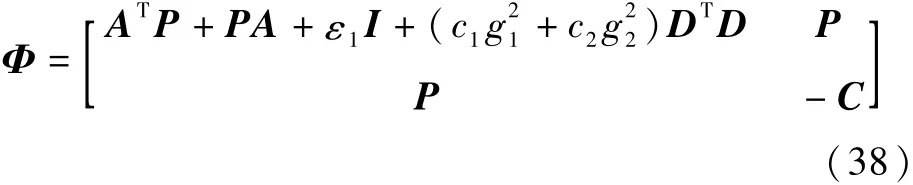
由分块矩阵的性质可以得到 Φ 为半负定矩阵。
选取类二次型Lyapunov函数V=ξTPξ,由式(29)和式(30)得

结合

可得

因此

由引理2可知,若k1*、k2*满足式(37),则ξ=在有限时间内收敛到0,即在有限时间内收敛到0,且收敛时间满足:
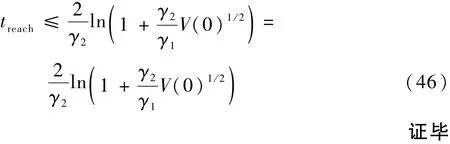
由定理1可知,对于未知常数g1和g2,存在满足式(37)约束的k*1和k*2使得x1和˙x1在有限时间内收敛到0。
定理2 当系统(26)满足假设3,控制器参数k1和k2满 足 式 (2 8),g1和g2为 未 知 数 时 ,x1和在有限时间treach内收敛到0。
证明
2)若k1<k*1,k2<k*2,选取类二次型Lyapunov函数:
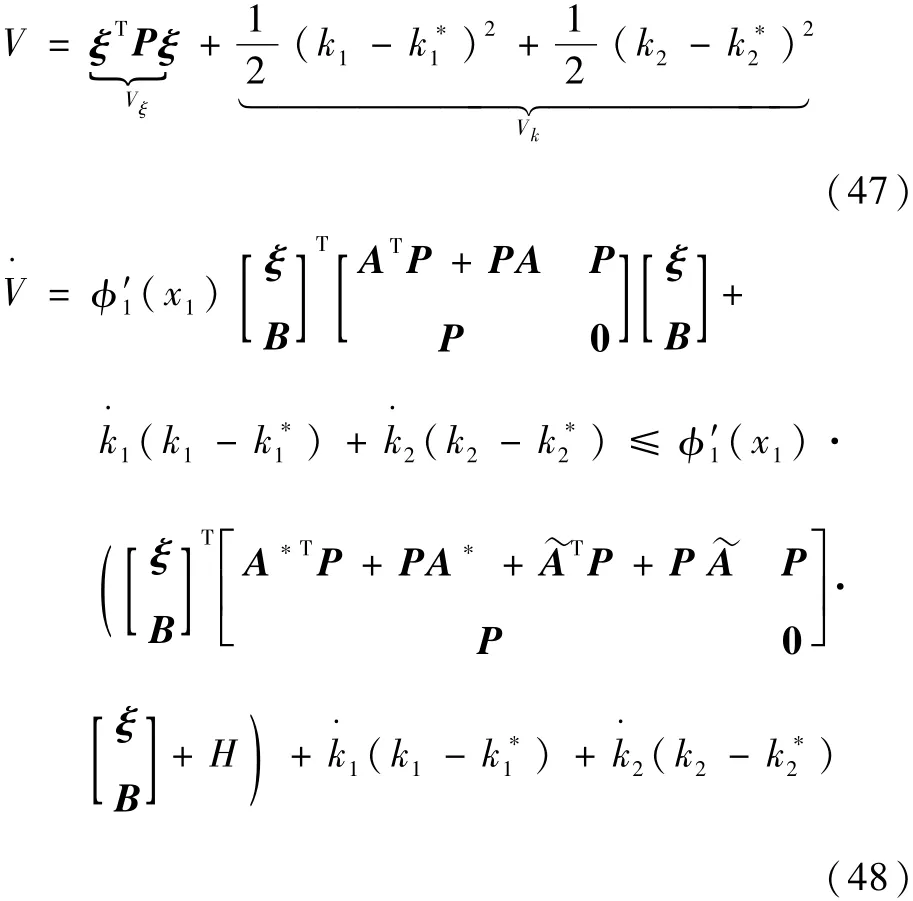
式中:
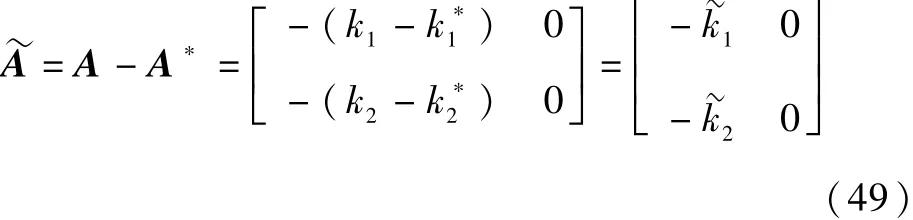
显然
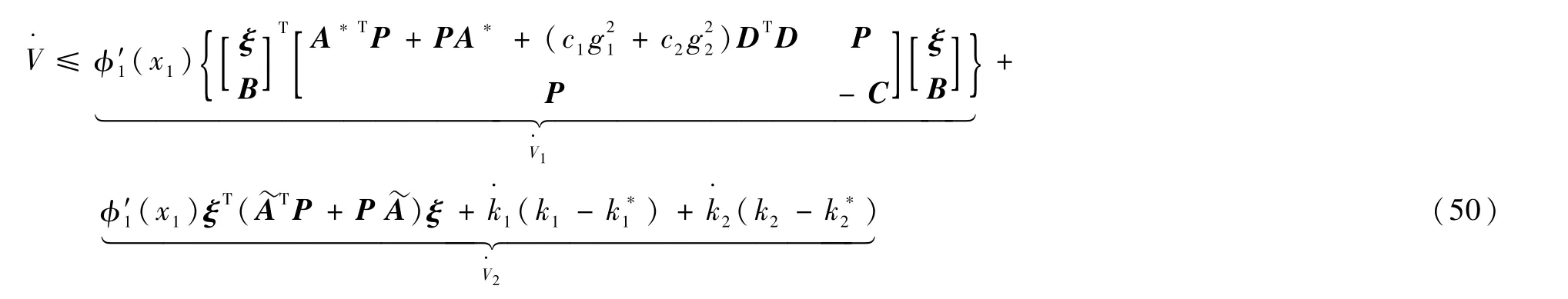
由定理1的证明过程可知:

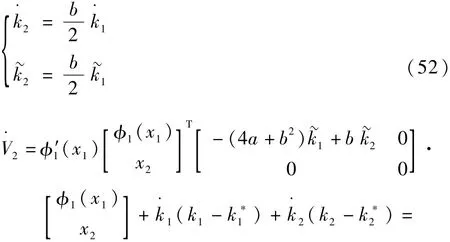
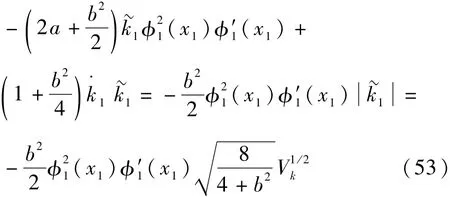
结合式(51),得到

式中:

于是有

式中:
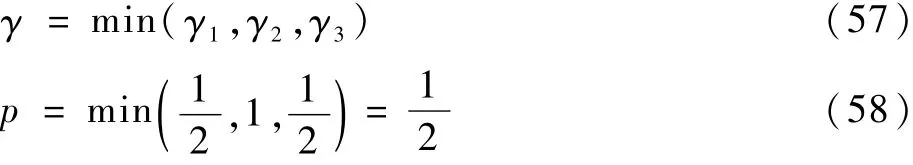
由引理1可知,系统(26)有限时间稳定,且收敛时间满足:
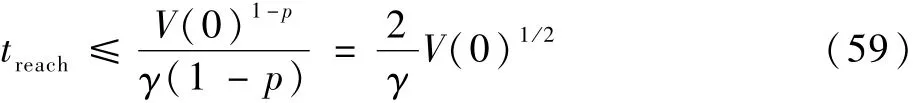
由于s很难严格收敛至0,而是在0的一个极小邻域内波动,使得k1和k2过大,进而引起系统不稳定。因此,将自适应参数控制器改进为

式中:ε2为很小的正数。
3 制导律设计

式中:c0=0.1。
结合式(7)可得

式中:

由定理3及式(9)得到FAST制导律为

式中:

其中:k1和k2的值满足式(60)。
FAST制导律对外界干扰具有鲁棒性,且能够在有限时间内收敛。由制导律的形式可以看出,参数k1和k2随着s的变化实时改变,且不需要已知外部干扰的上界。
4 仿真分析
为验证所提制导律的有效性,将FAST制导律 (Fast Adaptive Super-Twisting Guidance,FASTG)与自适应滑模制导律(Adaptive Sliding Mode Guidance,ASMG)、光 滑 二 阶 滑 模 制 导 律(Smooth Second Order Sliding Mode Guidance,SSOSMG)、ST制导律(Super-Twisting Guidance,STG)进行对比。其中,ASMG为一阶滑模制导律,其他为二阶滑模制导律,且4种制导律均采取式(61)作为滑模面。
ASMG为[17]

式中:k1=k2=2。
SSOSMG为[18]
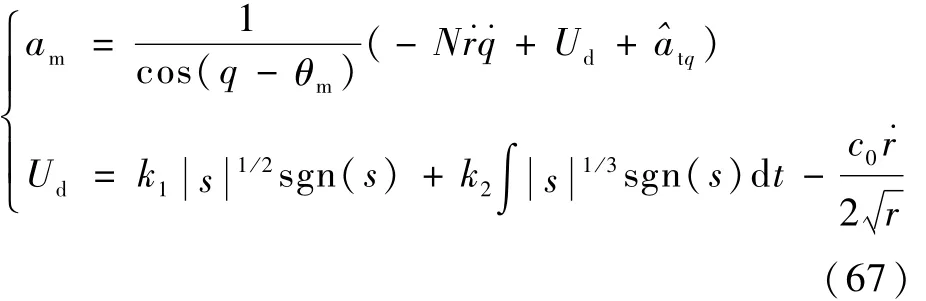
STG为[19]
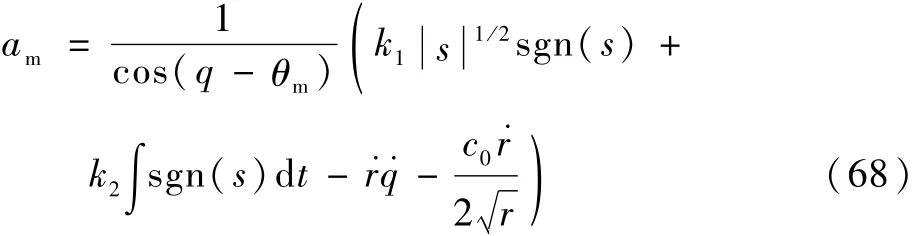
式中:k1=4,k2=3。
FASTG形式如式(64)所示,参数满足:a=0.5,b=1,c1=c2=1,ε2=0.1。
制导律所需的r、˙r、˙q等信息均由导弹导引头测量得到,且不考虑噪声和干扰。导弹自动驾驶仪视为理想环节,即不考虑延迟。仿真终止时间为弹目相对距离最近的时间点,仿真步长为0.01 s。
为了全面分析4种制导律的特点,分别在目标无机动和目标有机动2种情形下对制导性能进行比较。
4.1 目标无机动(情形1)
仿真条件:导弹初始位置为(0,0)km,初始速度为500 m/s,初速度方向为30°,初始过载约束为15g,切向过载为0,法向过载由制导律得到。目标初始位置为(10,5)km,初始速度为300 m/s,初速度方向为180°,切向过载和法向过载均为0。
MATLAB仿真仿真结果如表1和图2~图4所示。表1为情形1的仿真结果,其中Δ为脱靶量,treach和分别为滑模变量实际和理论收敛时间,tf为制导时间。图2为导弹弹道曲线,黑色虚线为目标运动曲线,绿色、黑色、红色、蓝色实线分别为ASMG、SSOSMG、STG、FASTG四种制导律下的导弹运动曲线。图3(a)和图3(b)分别为滑模变量s(t)及滑模变量的一阶导数˙s(t)变化曲线。图4为导弹法向过载变化曲线。
由图2及表1中的 Δ和tf可知,4种制导律的弹道平直且差异很小,制导时间接近,脱靶量STG最大,ASMG最小,SSOSMG和FASTG略高于ASMG,由于脱靶量远小于导弹杀伤半径,因此可视为直接命中目标。由图3及表1中的treach可知,4种制导律均能够在有限时间内使得s(t)及t)收敛至0,其中,FASTG收敛速度最快,STG和ASMG略慢,SSOSMG最慢且时间远大于其他方法。由此可以看出,FASTG在收敛速度方面较其他方法有一定的提高,但优势并不明显。由图4可知,在导弹发射的前5 s内,导弹过载a由大变小并逐渐稳定到0,其中FASTG的过载远大于其他制导律且变化最为剧烈,最大过载高于其他制导律4倍以上。
总之,在目标无机动的情形下,由于弹道接近直线,与其他方法相比,FASTG的脱靶量和制导时间相近,收敛速度最快,过载最大,其优势并不明显。
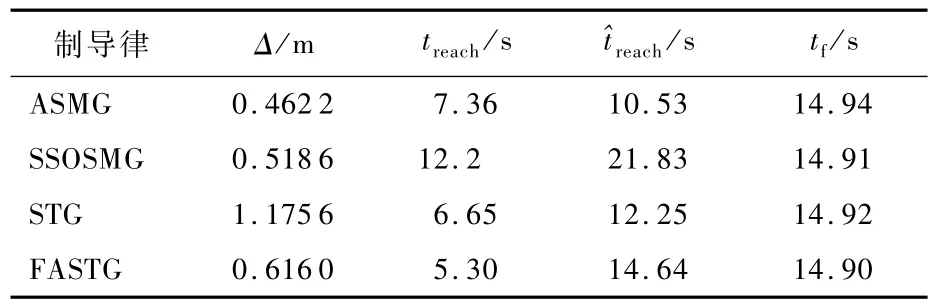
表1 仿真实验结果 (情形1)Table 1 Simulation experimental results(Case 1)

图2 导弹弹道曲线 (情形1)Fig.2 Missile ballistic curves(Case 1)

图3 滑模变量及其一阶导数变化曲线 (情形1)Fig.3 Variation curves of sliding-mode variable and its first-order derivative(Case 1)

图4 导弹法向过载变化曲线 (情形1)Fig.4 Variation curves of missile normal overload(Case 1)
4.2 目标有机动(情形2)
仿真条件:导弹初始位置为(0,0)km,初始速度为500 m/s,初速度方向为45°,最大过载为30g,切向过载为0,法向过载由制导律得到。目标初始位置为(2,2)km,初始速度为300 m/s,初速度方向为 0°,切向过载为0,法向过载nt=(5cos t)g。
MATLAB仿真结果如表2和图5~图7所示,其中曲线和变量含义与情形1相同。
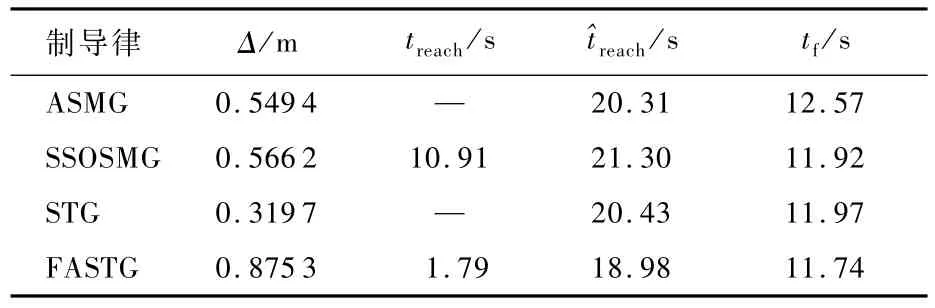
表2 仿真实验结果 (情形2)Table 2 Simulation experimental results(Case 2)

图5 导弹弹道曲线(情形2)Fig.5 Missile ballistic curve(Case 2)

图6 滑模变量及其一阶导数变化曲线 (情形2)Fig.6 Variation curves of sliding-mode variable and its first-order derivative(Case 2)

图7 导弹法向过载变化曲线 (情形2)Fig.7 Variation curves of missile normal overload(Case 2)
图5与图2相比,导弹弹道弯曲,其中ASMG最高,STG和SSOSMG次之,FASTG最低。表2中的脱靶量STG最小,ASMG和SSOSMG次之,FASTG最大,由于均远小于导弹杀伤半径,均可视为直接命中目标。制导时间FASTG 最短,ASMG最长,STG和SSOSMG介于两者之间。由图6可知,FASTG能够使得s(t)及˙s(t)在很短的时间内收敛至0,SSOSMG的收敛速度很慢,收敛时间接近制导时间,而ASMG和STG不能收敛,且s(t)大幅度波动。由此可见,FASTG在收敛速度方面明显优于其他制导律。由图7可知,由于s(t)的波动,过载在0附近上下波动。初始阶段,FASTG由于s(t)变化最为剧烈,因此过载最大。中间阶段4种制导律均小于5g。制导末段,STG和ASMG 的过载迅速增加并达到最大过载,FASTG的过载在10g左右,SSOSMG的过载为5g左右。
总之,目标机动情形下,弹道弯曲,FASTG制导时间最短,脱靶量相近,收敛特性明显优于其他方法,仅在初始阶段的过载较大。因此,FASTG在此情形下的表现更为优异。
5 结 论
1)在标准ST算法的基础上,增加了自适应参数控制器和线性项,提出了FAST算法。在系统不确定性上界未知的前提下,一方面控制器参数能够自适应调节,避免参数过大造成系统不稳定;另一方面系统在远离平衡点时具有更快的收敛速度,提升了标准ST算法的收敛特性。
2)利用二次型Lyapunov函数证明了FAST算法的有限时间稳定性,与其他证明方法相比,该方法计算较为简单,且能够得到收敛时间的估计公式。
3)将FAST算法成功地应用于制导律设计。仿真结果表明,本文算法在保留标准ST算法有效抑制抖振、鲁棒性强等优点的同时,具有快速收敛特性且不需要已知不确定性的上界,使得制导系统拥有更高的命中精度和稳定性。
