挂载飞行温度边界下固体发动机药柱结构响应分析

2019-07-31程吉明李进贤冯喜平朱国强

固体火箭技术 2019年3期

程吉明，李进贤，冯喜平，朱国强

(西北工业大学燃烧、热结构与内流场重点实验室，西安 710072)

0 引言

目前，无人机已经成为各军事强国重点发展的武器，无人机在现代战争中逐渐开始担任重要角色。机载导弹是无人机的主要作战装备，无人机在挂载飞行时，机载导弹会受到复杂的载荷作用，特别是高空巡航时环境温度极低，飞行过程中由于对流换热，发动机药柱会因降温收缩而产生较大的热应力/应变；同时，由于低温条件下推进剂力学特性变化，均会影响发动机药柱的结构完整性。

对于低温环境下推进剂药柱的力学性能，Chen[1]、赖建伟[3]及王哲君[3]等进行了一定的研究工作，研究认为低温环境下推进剂力学性能会发生较大变化，推进剂在拉伸过程中以基体断裂和颗粒脆断为主，与常温条件下相差较大。此外，由于无人机巡航飞行时间长，多次挂载飞行可能会对发动机药柱造成累积损伤，影响药柱的结构完整性。如王玉峰[4]、邓斌[5]等采用线黏弹性本构模型，结合线性累积损伤模型，对交变温度载荷作用下发动机药柱的结构响应及损伤特性进行了研究，结果表明，在温度循环作用下，推进剂药柱会产生累积损伤，损伤程度与载荷严酷程度相关。

本文以机载导弹发动机结构完整性为研究背景，针对不同挂载飞行环境下发动机药柱的结构响应特性展开研究，研究结果可为机载导弹发动机结构完整性评估及无人机挂载飞行制度提供参考。

1 计算模型

1.1 发动机计算模型

研究针对六角星形装药固体发动机，药柱外径为170 mm，绝热层厚度2 mm，壳体厚度3 mm。装药采用二维构型，并考虑到药柱大长径比特性，所以建立二维模型进行简化分析。由于发动机结构的对称性，因此以1/12几何结构作为分析模型，模型结构及网格如图1所示。

图1 星形装药发动机1/12计算模型

1.2 材料属性

模型计算时，发动机各部件材料属性见表1。

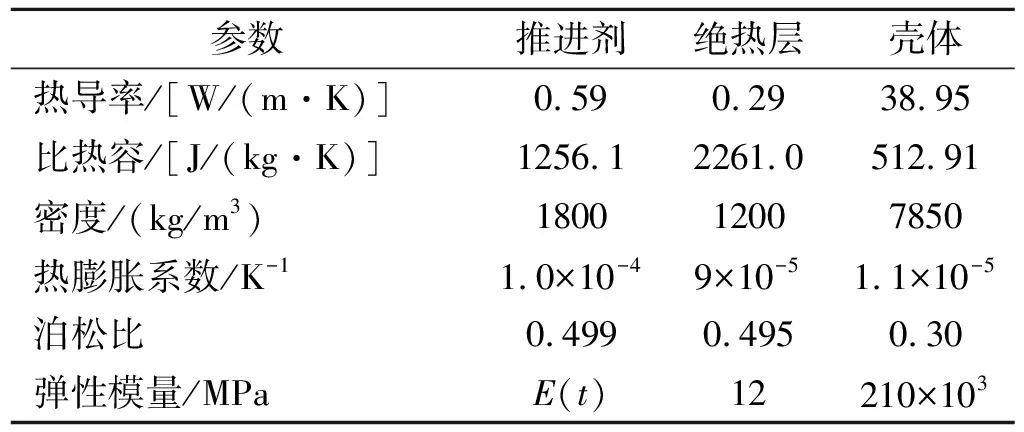
表1 发动机部件材料物性参数

固体推进剂采用线粘弹性本构模型，松弛模量采用n阶Prony级数表达式，并引入折算时间ξ考虑温度效应，时温等效因子aT采用WLF方程来描述。

通过HTPB推进剂不同温度下应力松弛试验，得到推进剂松弛模量主曲线，拟合得到松弛模量表达式各项系数如表2所示。

表2 HTPB推进剂松弛模量Prony级数表达式系数

同时，拟合得到表征推进剂时温等效因子aT的WLF方程：

式中T为温度，K。

1.3 载荷及边界条件

在挂载飞行阶段，因外界环境温度较低，发动机壳体与外界发生换热，药柱温度降低并形成热应力/应变。由于无人机巡航飞行为压音速，气动加热量相对较小，所以计算时不考虑气动加热，只考虑发动机壳体外表面与环境大气的对流换热。同时，研究不考虑固化降温载荷及振动载荷等对发动机药柱的影响。

通过设计不同的飞行工况如表3所示，对比分析不同巡航速度(工况1～4)及飞行高度(工况5、2、6)对发动机药柱结构响应的影响。

表3 计算工况

发动机初始温度为293 K，发动机壳体外表面施加对流换热边界条件，两对称面施加对称约束边界条件，药柱、绝热层和壳体施加绑定约束条件。

挂载飞行过程中发动机壳体外表面与大气之间的对流换热简化为外掠平板换热模型，根据边界层型对流换热模型确定发动机壳体表面的对流换热系数。边界层内流动根据雷诺数Re的不同分为层流边界层和湍流边界层，根据表3飞行工况，计算得到不同飞行工况下的雷诺数Re均大于5×105。因此，认为平板上的边界层由层流段和湍流段组成，其对流换热系数h可采用下式计算[11]：

式中Pr为大气普朗特数；λ为大气热导率；l为平板特征长度，计算时取1 m。

在某个温度下，大气的Pr和λ可依据标准大气表[14]插值计算得到，计算得到不同工况下对流换热系数如表4所示。

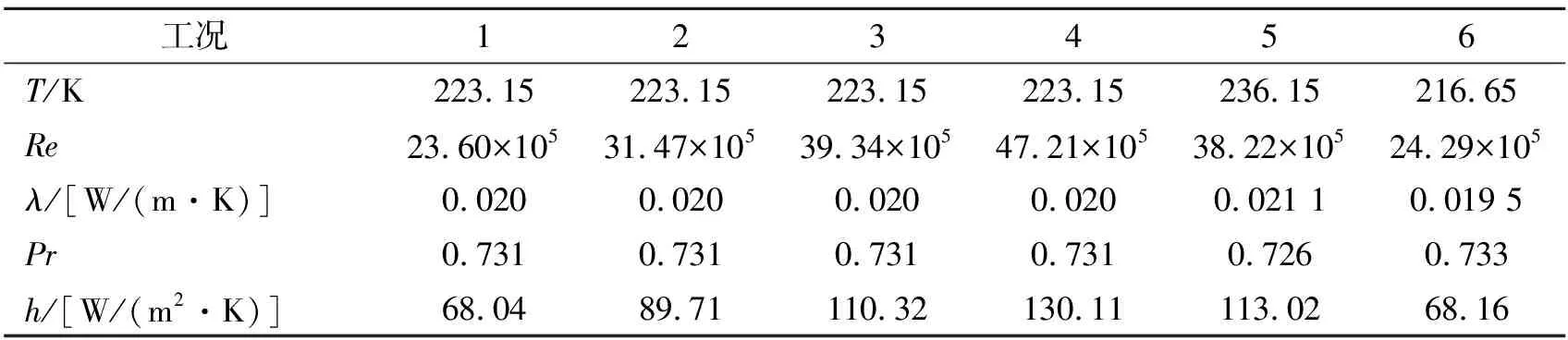
表4 不同计算工况下的对流换热系数

2 计算结果与分析

不考虑固化降温载荷作用，单独考虑挂载飞行条件下发动机换热过程，计算了发动机在10 km高度以400 km/h巡航速度条件下飞行6 h后的推进剂药柱温度、应变和应力分布，如图2所示。星角根部A点和星尖B点温度和等效应变随时间的变化关系如图3所示。从图2和图3可见，在飞行6 h后药柱温度场分布基本达到均匀，药柱中最大温度偏差不超过1 K。在挂载飞行温度边界条件下，推进剂药柱在星角根部A点处应力应变达到最大，最大等效应变为9.0%，而星尖部位由于可以相对自由移动，因此应力、应变相对较小。

(a)温度 (b)等效应变 (c)Mises 应力

(a)温度 (b)等效应变

2.1 不同飞行速度下药柱结构响应

计算了发动机在10 km高度不同巡航速度下的结构响应，得到了药柱星角根部节点A温度和等效应变随时间的变化曲线，如图4所示。可以看出，随巡航飞行速度增加，药柱在飞行初期降温速率加快，但随巡航时间的增加，药柱温度场逐渐趋于均匀，各巡航速度下药柱温度与外界环境温度趋于一致。

总体来看，巡航飞行速度对药柱结构响应的影响相对较小，主要影响挂载飞行初期药柱温度和应力应变的变化速度。提升巡航速度，主要通过改变发动机壳体与外界环境的对流换热系数来影响发动机温度场分布。飞行速度越快，对流换热系数越大，飞行过程中药柱温度下降越快，对应的热应变也越快增大。当药柱温度场趋于平衡时，对应的发动机药柱最大等效应变为0.09左右，不同巡航速度下挂载飞行6 h后，药柱的最大等效应变偏差较小，不超过2%。

2.2 不同飞行高度下药柱结构响应

在飞行时间足够长的条件下，对发动机药柱结构起主导作用的是外界环境温度。图5给出了不同飞行高度下以400 km/h速度巡航时发动机药柱星角根部节点A的温度和等效应变随时间的变化曲线。可看出，随飞行时间的增加，药柱平衡温度逐渐降低并与外界环境温度基本保持一致。随飞行高度的增加，外界环境温度逐渐降低，对应的药柱在挂载飞行条件下产生的热应变也越大，星角根部A点等效应变由8 km时的0.074，到12 km时增加到0.098。

(a)温度 (b)等效应变

总体来说，改变飞行高度实际上是改变发动机外界环境温度来影响药柱结构响应。相对于8 km高度飞行6 h时药柱的最大等效应变，在10 km高度飞行6 h最大等效应变相对增大21.6%，12 km高度飞行6 h最大等效应变相对增大32.4%。可见，改变巡航飞行高度对药柱结构影响较大。

此外，由计算结果可以发现，发动机在挂载飞行温度边界条件下，药柱会产生较大的应变，多次挂载飞行相当于发动机药柱经历循环载荷作用。因此，多次挂载飞行必然会对发动机药柱造成累积损伤，影响发动机药柱的结构完整性。

2.3 多次挂载飞行条件下药柱累积损伤分析

考虑推进剂药柱在多次挂载飞行条件下的渐近损伤，参考文献[10]中HTPB推进剂蠕变破坏试验数据，采用蠕变损伤模型来定义累积损伤函数为[6]

式中α和β为损伤函数参数，可根据推进剂蠕变损伤破坏试验拟合获得；aT为时温等效因子，由WLF方程确定。

根据渐近损伤准则，当D(t)≥1时，认为药柱结构失效。根据文献[10]中HTPB推进剂蠕变破坏试验数据，拟合得到α=1.08，β=8.025。

从图2可知，发动机在挂载飞行6 h后，推进剂药柱温度分布基本达到均匀，并与外界环境温度一致，药柱应力应变也达到最大。因此，分别计算了发动机药柱在10 km高度以400 km/h速度挂载飞行6 h和10 h后推进剂药柱的结构响应，挂载飞行结束后，发动机293 K地面12 h，完成一个挂载飞行周期。计算得到了发动机在多个挂载飞行周期下推进剂药柱损伤值随时间的变化曲线，如图6所示。

由于推进剂本构模型未考虑非线性损伤效应，因此在飞行结束发动机返回地面后，当药柱温度恢复到环境温度时，药柱应力应变也恢复到初始状态，此时损伤值保持不变。从图6可知，当考虑推进剂的渐近损伤特性时，计算得到的药柱损伤值随挂载飞行次数的增加而逐渐增大。改变飞行制度，延长巡航飞行时间，将单次挂载飞行时间由6 h增加到10 h，单次飞行造成的推进剂药柱损伤值增大。由此可见，改变飞行条件，药柱的损伤特性也会发生改变。

图6 多次挂载飞行条件下药柱累积损伤

由于不同配方体系的复合固体推进剂力学特性差异较大，因此本文采用参考文献中HTPB推进剂的蠕变损伤数据计算得到的推进剂损伤特性与实际情况会有较大偏差。如果进一步通过松弛破坏试验和蠕变破坏试验获得固体推进剂的精确累积损伤模型，即可开展推进剂药柱在不同挂载飞行条件下的损伤特性分析，为机载导弹挂载飞行制度设计以及挂载飞行药柱结构完整性评估提供指导，避免药柱在多次挂载飞行后发生结构失效。