固体推进剂药柱局部夹杂应力场分析的边界元法
2019-07-31黄拳章强洪夫王学仁岳春国李爱华
黄拳章,陈 健,强洪夫,王学仁,岳春国,李爱华
(1. 火箭军工程大学,西安 710025;2. 陕西师范大学,西安 710062)
0 引言
固体推进剂药柱在浇注、固化降温、长期贮存过程中,由于工艺、残余应力和环境等因素的影响,不可避免地会出现夹杂、孔隙、脱粘、裂纹等缺陷形式[1-3],这些缺陷是困扰固体火箭发动机质量、寿命和使用性能提高的重要因素。由于脱粘、夹杂和推进剂界面材料不连续,在发动机点火发射时高温、高压和高过载的作用下,夹杂和孔隙附近将出现局部高应力、应变区域,过高的应力、应变将会导致推进剂的脱湿、裂纹萌生和界面脱粘,而裂纹失稳扩展将会导致固体火箭发动机蹿火,甚至爆炸等灾难性后果[4]。因此,在固体火箭发动机药柱结构完整性分析中,必须给予十分的关注和重点评估。为了获得精确的应力-应变场,传统有限元法通常采用网格局部加密的手段提高精度,由于药柱几何形貌复杂,且缺陷尺寸太小,势必会带来网格划分的困难和巨量的计算耗费。
边界元法具有精度高、适合复杂边界形状和降维求解等优点。因此,本文引入边界元法,在固体推进剂药柱高精度局部应力-应变分析中作为有限元分析的重要补充。
1 夹杂问题的数学模型
首先,对含有夹杂、孔隙的固体推进剂药柱受力问题进行抽象和简化,将药柱抽象成一个均匀的物体域,其内部的颗粒和孔隙统一抽象为夹杂,建立如图1所示的数学模型。图1中,线弹性固体介质内含有n个任意形状的夹杂或孔隙。其中,固体区域和其相应的外边界分别为Ω和Γ,各夹杂区域和相应的边界分别为Ω1,Ω2,…,Ωi,Ωn和Γ1,Γ2,…,Γi,Γn。另外,Γt和Γu分别为给定的面力边界和位移边界。此时每个夹杂不仅受外载荷的影响,还与相邻夹杂(孔隙)之间发生相互作用,其受力状态非常复杂。基体域与夹杂域之间相互作用,其界面上的位移和面力都是未知的,因此该问题不能直接求解。但考虑到界面位移和面力是受夹杂自身本构所控制的,因此它们并非是相互独立的,只要找到两者之间的函数关系,并将其作为已知边界条件的补充条件,就能使原问题得到解决。基于此,本文建立了孔隙和固体夹杂与基体界面位移与面力的关联矩阵,将其代入到基体子域的边界元离散代数方程组中,以求解各夹杂边界的位移和面力。

图1 夹杂问题简化模型
2 边界元方法
2.1 基本方程
对于如图1所示平面夹杂问题,如果不计体力,则边界积分方程可写成下列形式:
(1)

对于弹性力学平面应变问题,基本解和相应面力可写为[5]
(2)
(3)
为了对积分方程进行数值求解,将所有边界离散成若干个边界单元,在每个边界单元上对位移和面力分别进行插值。进一步在方程(1)中将p点依次取为离散边界上的各个结点,整理后,可得到下列形式的线性代数方程组:
A0x0=B0y0
(4)

(5)
式(4)中系数矩阵A0和B0可用分块形式表示:
(6)
式(6)中,分块矩阵下标的含义为:第1和第2下标分别表示源点p和场点q所在的边界线的类型;下标“1”表示该段边界给定了面力边界条件;“2”表示该边界段给定了位移边界条件;“3”表示该边界为基体与夹杂的交界面;第1上标和第2上标分别表示源点和场点分别在第几个夹杂界的面上,其中“0”代表基体的外边界。
由于各夹杂界面的位移和面力都是未知量,使得式(4)中未知量的数目大于方程数,因此该方程不能定解。但考虑到夹杂表面位移和面力之间并不是相互独立的,在线弹性框架内,两者服从下列线性关系:
Tjj=DjUj
(7)
式中Tjj、Uj和Dj分别为第j个夹杂与基体界面靠近夹杂一侧的面力、位移以及它们之间的关联矩阵。
夹杂与基体界面靠近基体一侧的面力T0j和Tjj是一对作用力和反作用力,则有
T0j=-Tjj=-DjUj
(8)
将式(8)代入式(4),就可求得基体子域边界的未知位移和面力,进而可求出基体和夹杂域内任一点的位移、应变和应力。
需要指出的是,以上公式是针对线弹性问题的,如果是粘弹性问题,则可根据弹性-粘弹性对应原理解决[6]。但对应原理需将粘弹性材料转换成一系列的弹性材料,进而求解不同材料参数的弹性解,因此边界元离散方程的系数矩阵将需要不断更新,从而导致计算量成倍增加。此外,弹性-粘弹性对应原理对于非同质材料瞬态温度问题以及边界条件是时间的复杂函数的情况并不适用。基于此,本文采用Prony级数法描述粘弹性材料的本构关系,并将粘弹性效应以初应力的形式作为方程的右端项,进而给出时间域内粘弹性边界元积分方程以及应力求解的迭代公式,使得边界元方程系数矩阵在求解过程中始终保持不变,并用数值迭代方法进行求解,可同时计算出域内和边界不同位置的应力和应变值。
不考虑体力和热应力,则粘弹性问题的粘弹性边界积分方程为[7]
(9)

(10)

(11)
(12)
(13)
(14)
(15)

(16)
式中,G为剪切模量;K=E/3(1-2ν)为体积模量;ξ和ξ′分别为受温度影响的减缩时间,当材料不受温度影响时,ξ=t,ξ′=t′。若温度是连续变化的,则有
(17)
式中aT为移位因子,其大小可由实验确定。
假设将边界离散为n个单元,每个单元m(m>1)个节点,则令p点位于各个不同的边界节点,则对式(9)进行数值积分后可形成关于节点未知量的方程组,如式(18)所示。
[H]2n×2n(m-1){u}2n(m-1)=[G]2n×2n(m-1){p}2n(m-1)+
(18)
(19)
将方程(18)中的未知量移到方程左边,已知量移到右边,可得
(20)

2.2 夹杂界面位移与面力的解耦
式(7)建立了夹杂界面面力与位移的线性关系,因此实现夹杂界面面力与位移解耦的关键是建立杂边界面力与位移的关联矩阵,这取决于夹杂材料的本构关系。下面分别按固体夹杂和孔隙两种情况,详细介绍夹杂界面面力与位移的解耦过程。
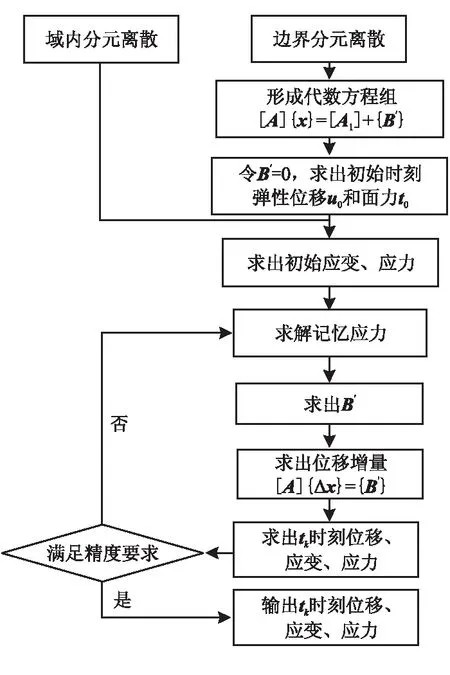
图2 粘弹性边界元迭代算法流程图
2.2.1 固体夹杂
对于固体夹杂子域,可列出边界积分方程如下:
(21)
将固体夹杂子域边界进行分元离散后,由式(21)可得下列代数方程组:
(22)

由式(22)可得
(23)
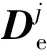
2.2.2 孔隙和刚性夹杂
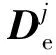
2.3 夹杂边界的几何近似
固体推进剂药柱是通过固体推进剂搅拌浇注而成的,混进的夹杂颗粒以及推进剂配料如AP颗粒等经过大量的滚动和摩擦,棱角基本磨平,最终成球形的居多。因此,可将夹杂和孔隙近似为球形,二维情况下,可将夹杂和孔隙处理成圆形。而对于孔隙状孔隙,则可用长细比较大的椭圆形进行近似。而为了几何建模和网格划分的方便,椭圆边界可用四段两两相切的圆弧近似描述[8],如图3所示,切点分别为C1、C2、C3、C4,可证明每两段弧的切点是唯一的。椭圆的长、短半轴分别为a和b,4个顶点依次为A1、A2、A3、A4。圆弧1和4的圆心分别为O1和O4,曲率半径分别为R1和R4,且有圆弧1、4关于y轴对称以及圆弧2、3关于x轴对称。
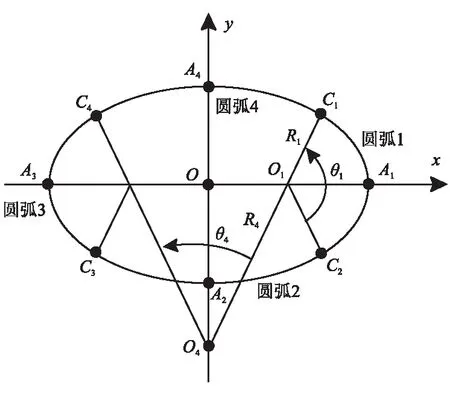
图3 椭圆孔的几何近似
3 数值算例
3.1 中心含单个圆形夹杂的平面问题
考虑如图4所示对边受均匀压力P作用的含单个圆形夹杂的平面应变问题,设板的边长为a,夹杂半径为r。基体的弹性模量E=2 GPa,泊松比ν=0.3,为了限制整体刚体位移,将平面左、右两边中点的竖直方向位移和上边界中点的水平位移加以约束。
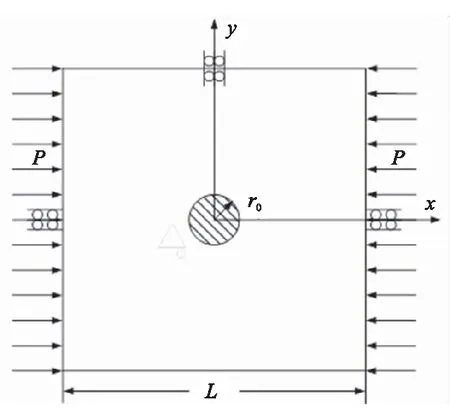
图4 中心含单个圆形夹杂的平面
假设夹杂为线弹性材料,弹性模量E1=1.2E,泊松比ν1=ν,a=1000 mm,r=0.5 mm。由于夹杂的尺寸远小于方板的尺寸,因此本算例可近似为无限大问题,则正确的数值解将趋近于解析解。求解时,将方板的四条边界各均匀划分40个线性直线型单元,夹杂边界均匀划分48个线性圆弧单元[9]。图5给出了平面应变状态下,固体夹杂界面径向位移和径向应力随弧长的分布曲线,弧长沿顺时针走向为正,起点弧度为π/2。由图5可看出,边界元解和解析解吻合很好,说明本文的算法和程序都是正确的。

(a)径向位移

(b)径向应力
3.2 圆筒固体火箭发动机燃烧室平面应变问题
如图6所示,圆筒型固体火箭发动机平面应变问题。
设发动机内腔半径为r0,壳体内外径分别为r1和r2,壳体厚度为h=r2-r1。药柱材料为典型的粘弹性材料,假设壳体材料为弹性材料,因为绝热层和衬层的很薄,且材料性质与药柱相似。为简单起见,这里忽略绝热层和衬层的厚度。发动机内腔受到压力q(t)作用,如图7所示。

图6 圆筒发动机燃烧室平面应变模型

图7 瞬时压力模型
(24)
假设固体推进剂和发动机壳体的泊松比分别为ν和νk;E(t)和Ek分别为固体推进剂和发动机壳体的弹性模量;m=r1/r0为药柱外内径比。根据粘弹性解-弹性解对应原理进行理论解析解的计算,可得药柱内径r0处的粘弹性解[10-11]。

为简单起见,先不考虑体力和热应力,则由式(18)可知,在区域Ω1上有
(25a)

同理,在区域Ω2上有
(25b)

假设壳体和药柱粘接完好,则壳体和药柱在公共边界Γ1上满足位移和面力的连续条件:
(26)
由式(26)可知,式(25a)和式(25b)可分别改写成下列形式:
(27a)
(27b)
综合式(27a)和式(27b)可得到下列形式:
(28)
式(28)即是圆筒型固体火箭发动机平面应变问题的代数方程组,按照2.1节的边界元离散方法和记忆应力迭代解法,即可求出该问题的解。此外,从该方程的形式也可看出,该方程系数矩阵具有带状特征,也可克服边界元系数矩阵是满阵的缺点,从而可节约内存并减少计算时间。
采取线性圆弧单元对图6所示的模型进行离散,如图8所示,1/12对称模型,边界Γ0、Γ1和Γ2上共划分4个圆弧单元,一周共48个单元,为计算记忆应力和内点的应力应变,将药柱区域和壳体划分成四边形等参单元(采用有限元网格),其中药柱内划分28个四边形网格,壳体内划分8个四边形网格,完整域内一共432个四边形网格,模型的两个侧边施加对称性边界条件,区域积分采用3×3高斯积分。
计算模型载荷参数、几何参数和材料参数如下:
载荷参数:q0=8.9 MPa,t0=0.1 s;
模型尺寸:r0=0.3 mm,r1=1 mm,h=0.005 mm;
材料参数:Ek=206.8 GPa,νk=0.3,推进剂ν=0.495,初始模量E(0)=12.209 MPa。
松弛模量的Prony级数形式如下:
(29)
其中,τi=4×10(i-3),剪切模量和体积模量计算式如下:
(30)

图8 网格划分示意图

图9 周向和径向应力随时间的变化

图10 周向和径向应变随时间的变化
对粘弹性材料进行数值计算时,一般假设体积模量为常数,并取K(0)作为体积模量,这样计算式(16)的遗传积分时就可以简化,只需计算记忆应力随着剪切模量变化即可。图9和10分别给出了周向和径向应力、应变的解析解和数值解随加载时间的变化曲线,从中可看出两者吻合良好。
4 结束语
本文给出了粘弹性时域问题的边界元法和求解含孔隙和固体夹杂问题的边界元求解方案,通过算例验证了方法的正确性和有效性。该方法可推广到一般的三维问题,对于固体推进剂药柱中含孔隙和颗粒夹杂的情况,则可精确计算夹杂界面局部的应变场和应力场,可为固体推进剂药柱的结构完整性分析提供精确的数据。但传统边界元法的系数矩阵是非对称的满阵,求解代数方程组一般采用高斯消去法或迭代法,使得计算效率受到很大限制,进而影响了计算规模,下一步可通过引入快速多极边界元法,以提高计算效率。
