双脉冲发动机EDPM软隔层含率相关能量限制器的黏超弹本构模型
2019-07-31范兴贵许进升
范兴贵,许进升,陈 雄
(南京理工大学 机械工程学院,南京 210094)
0 引言
级间隔离技术作为双脉冲固体火箭发动机(以下简称双脉冲发动机)的关键技术之一,其技术突破成为双脉冲发动机实现工程应用的关键。双脉冲发动机级间隔层装置不仅要求具有良好的绝热能力,还要保证安全可靠地打开。国内对双脉冲发动机的隔层开展了大量的试验和仿真研究[1-4]。对于隔层式双脉冲发动机而言,隔层必须保证在II脉冲工作时能够顺利打开,打开压强一致性好。为此,国内的许多研究人员对双脉冲发动机II脉冲的工作过程进行了数值模拟[5-6],在对软隔层进行建模时,通常将EPDM假设为线弹性或者超弹性材料来建模。然而,EPDM软隔层在双脉冲发动机工作过程中的力学行为已经不再属于线弹性或超弹性,具有材料非线性、几何非线性、加载率相关性等非线性黏弹性材料的特点。因此,为了真实研究隔层在破坏过程的各种特性,有必要对EPDM软隔层的本构模型进行研究。
目前针对橡胶类材料,已经建立了许多黏超弹本构模型[7-12],这些研究者建立的本构模型描述的是理想材料的黏超弹性力学响应。对于实际的橡胶类材料来说,当应变能累积到一定的极限后,橡胶类材料会发生失效而断裂,传统的描述橡胶类材料的本构模型是无法描述这一行为的。为了更准确地描述EPDM软隔层从开始工作到失效的整个过程,有必要建立包含失效的本构模型。本文所建立的考虑失效的本构模型是基于原子势的连续介质力学模型,这种方法的基本思想是建立一个包含能量限制器的应变能函数,从这个应变能函数可以自然地推导出考虑材料失效的黏超弹本构模型。这个模型首先由Volokh等[13]在研究各项同性脆性材料的本构模型时提出。Volokh[14]、Trapper[15-16]等又将此模型应用于描述生物组织力学行为的本构模型中。在后来研究中发现,之前提出的应变能函数更适用于描述生物软组织的渐进失效行为,而对于橡胶这种失效时转变比较剧烈的材料来说,需要引入新的可以调节失效时转变剧烈程度的应变能函数。因此,Trapper等[17]将上不完全伽马函数引入到了应变能函数中,通过调节相应的参数可以调节失效时的转变剧烈程度。然后作为验证,他采用此模型模拟了刚性弹丸侵彻天然橡胶薄板的试验。前面介绍的本构模型在卸载时会出现应变软化可逆的问题,为了解决这个问题,Volokh等[18]又提出了一个新的应变能函数,使得当材料内部累积的应变能达到临界值时,材料的失效不可逆转。关于含能量限制器的超弹模型的研究进展可以看Volokh写的综述[19]。以上介绍的模型都未考虑应变率效应,为了描述具有黏超弹性的材料的失效行为,Volokh等[20]将含有能量限制器的应变能函数引入到一个准线性黏弹性本构模型中,使得建立的模型可以描述材料失效强度的率相关效应。Aranda等[21]在Volokh提出的失效不可逆的应变能函数的基础上,考虑应变率效应,建立了一个考虑材料失效的非线性黏超弹本构模型,并对Fatt等[22]在高应变率下的单轴拉伸试验结果进行了数值模拟。
Volokh等通过引入了能量限制器这一概念,较好地描述了橡胶类材料在大变形时的失效行为,但是其建立的本构模型却无法描述某些橡胶类材料的断裂伸长率随加载速率的增加而增加的现象。本文针对这一不足,在其建立的含率无关能量限制器的黏超弹本构模型基础上,通过在能量限制器φ中引入率相关项,使其能够预测断裂伸长率随加载速率的增加而增加的现象,从而为双脉冲发动机软隔层的打开过程数值仿真提供理论模型。
1 试验结果与分析
本文所研究的对象是某种双脉冲发动机用的EPDM软隔层,厚度为5 mm,该材料需要在EPDM基体中加入填充性纤维(如酚醛纤维、芳纶纤维等)以及阻燃性添加剂(无机阻燃剂、有机阻燃剂和复合阻燃剂)来提高其热稳定性能和耐烧蚀性能。根据航天工业行业标准GB/T 528—2009,将EPDM软隔层制成哑铃型3型标准试件,该试件标距 为16 mm,截面尺寸为4 mm×5 mm。试件尺寸如图 1所示。

图1 哑铃型试件尺寸示意图(单位:mm)
试验在微机控制电子万能材料试验机上完成,试验室的环境条件为:温度25 ℃,湿度40%。进行了单轴等速拉伸试验。单轴等速拉伸速率分别为1、10、100、500 mm/min。试验中对每一个工况进行多次重复试验,并选取5次有效试验结果的平均值作为该工况下的试验曲线,单轴等速拉伸的试验结果如图 2所示。
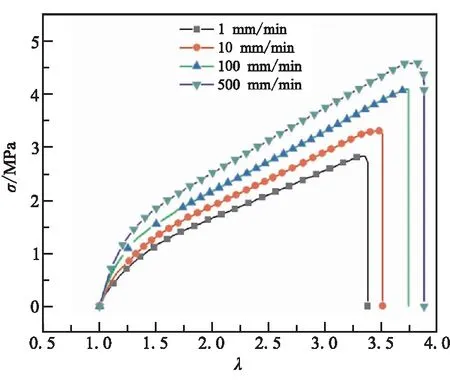
图2 不同加载速率下的试验结果
从图 2中可看出,EPDM软隔层表现出软而韧的特点,没有比较明显的屈服现象。从断裂类型来看,常温下的EPDM软隔层为高弹态,其断裂类型一般属于韧性断裂中的高弹断裂;从断裂伸长率来看,在准静态加载的条件下,EPDM的断裂伸长率呈现出较为明显的率相关效应,即断裂伸长率随着加载速率的增加而增加;从断裂强度来看,和其他硬而韧的高聚物(如尼龙、聚碳酸酯等)相比,其断裂强度较低,加载速率为500 mm/min时仅有4.5 MPa左右。从图2还可看出,当伸长比大于1.5之后,从单条曲线来看,工程应力-伸长比曲线呈现出线性关系。
2 改进的含能量限制器的黏超弹本构模型
2.1 含率无关的能量限制器的黏超弹本构模型
小变形条件下,黏弹性材料的力学响应可以用标准线性固体模型来描述[23],对于大变形的情况,仍然可以采用相似的模型,如图3所示。

图3 黏超弹本构模型
(1)
其中
自由能ψ可以分解为

(2)
对于大变形不可压缩的橡胶材料来说,式(1)可以改写为
(3)
对于应变能函数ψ(C),若考虑含有能量极限,则可以写为[14]
(4)
式中Γ(s,x)为上不完全伽马函数;W(C)为未损伤超弹性材料的应变能密度函数;φ为能量限制参数;m为无量纲材料常数,反映了材料过渡到完全失效的转变快慢程度。
由求导的链式法则,可得
(5)
经过求导运算后,可得
(6)
这里W(C)采用Exp-Ln应变能函数,W可为[25]
(7)
其中,A=G/2,G为橡胶材料的剪切模量,A、a和b决定了橡胶类材料在小、中和大应变阶段的力学响应。
这里定义ψ1为
(8)
则式(3)为
(9)
对于单轴加载的情形,假设加载方向上的伸长比为λ11=λ,则其余两个主方向的伸长比为λ22=λ33=λ-1/2,则变形梯度张量F可表示为
(10)
相应的左柯西-格林应变张量B=FFT可表示为
(11)
将式(11)代入式(9),可得三个方向的主应力分别为
(12)
(13)
单轴加载的边界条件为σ11=σ,σ22=σ33=0,联立式(12)、(13)可得加载方向的柯西应力σ11:
(14)
其中,m(t-τ)为松弛函数,可写为Prony级数形式(取N=2):
(15)
(16)
2.2 含率相关的能量限制器的黏超弹本构模型
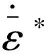
(17)
(18)
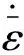
(19)
(20)
(21)
3 模型验证及敏感性分析
3.1 模型验证
式(21)中一共包含有13个参数,这13个参数的获取过程分为两步:首先,选择1 mm/min的单轴等速拉伸曲线采用MATLAB自带的遗传算法工具箱结合最小二乘法进行拟合,求出参数β∞、β1、θ1、β2、θ2、A、a、b;然后,根据断裂伸长率采用同样的拟合方法求出m、φ0、A、B和η,拟合结果如表 1所示。表2为失效的相关参数,拟合结果与试验结果的对比如图 4所示。

图4 1 mm/min试验结果与拟合结果对比

β∞β1θ1β21.475 40.471 5106.511 62.660 2θ2Aab0.328 60.347 80.011 90.114 3

表2 失效相关参数
为了验证所建立的模型的预测能力,选取10、100、500 mm/min的单轴等速拉伸曲线来进行验证,预测结果与试验结果的对比如图 5所示。

图5 预测结果与试验结果对比
从图5可看出,将能量限制器作为加载速率的函数之后,除了能预测到断裂强度随加载速率的增加而增加外,模型还能够预测到EPDM软隔层的断裂伸长率随着加载速率的增加而增加的现象,预测结果与试验结果良好的一致性说明了本文建立的本构模型的合理性。
3.2 敏感性分析
本文只讨论模型参数变化对断裂伸长率影响,由于影响断裂伸长率的只有指数项,所以只讨论参数m、φ0、A、B和η,模型参数的拟合结果作为参数基准值,每个参数变化分别为±0.1、±0.2、±0.3、±0.4、±0.5,每个参数变化引起的断裂伸长率的相对变化率定义为
(22)
每个参数变化时的断裂伸长率的相对变化率如表3所示。
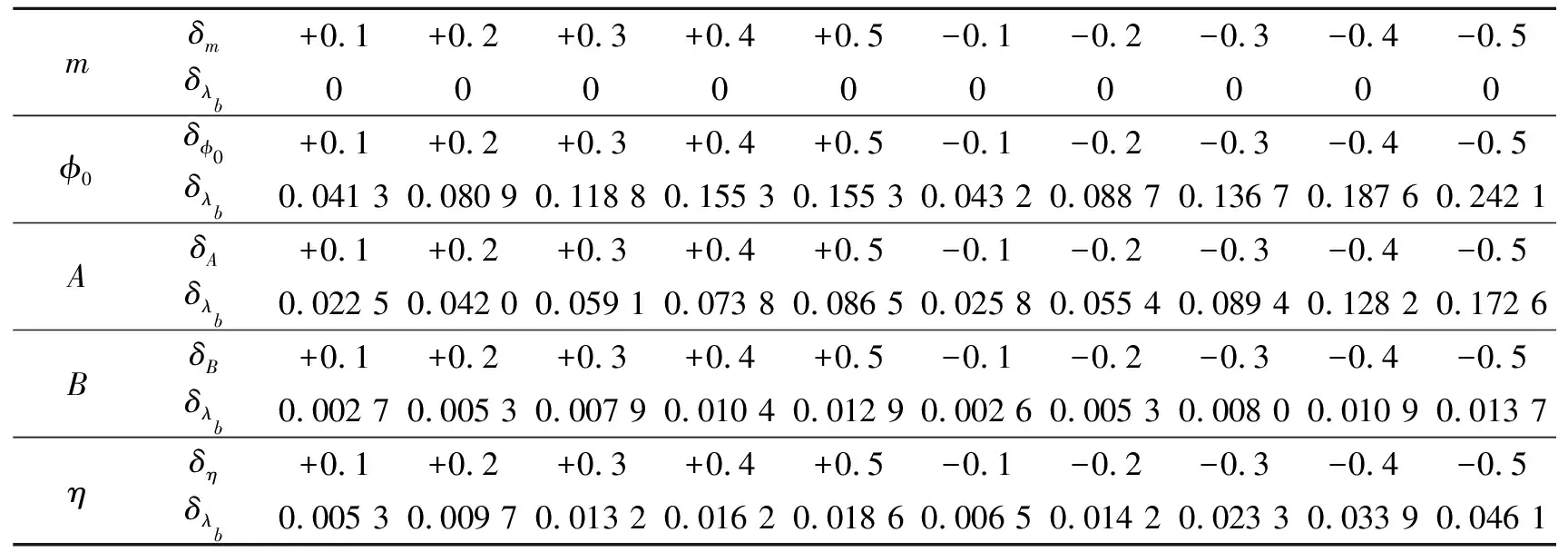
表3 m、φ0、A、B和η变化时断裂伸长率的相对变化率
从表3可看出,由于参数m的值很常大,且位于指数项中,导致m值减小为原来的一半时,m对λb几乎没有影响。剩余4个参数中,λb对φ0最敏感,δλb最大达到0.24,其次为A,最低的是B和η,δλb最大值均小于0.1。
4 结论
(1)对双脉冲发动机EPDM软隔层低应变率条件下的力学行为进行了研究,获取了EPDM软隔层在低应变率加载下的试验曲线。从试验结果来看,EPDM软隔层具有超弹和黏弹性材料的特点,相同应变下,加载速率越大,对应的载荷值越大。
(2)针对含能量限制器的本构模型无法描述EPDM软隔层的断裂伸长率随着加载速率的增加而增加的现象,本文将能量限制器作为加载速率的函数,建立了含率相关的能量限制器的黏超弹本构模型,利用单轴拉伸试验的数据结合最小二乘法获取了模型参数。
(3)对建立的本构模型进行了参数敏感性分析。分析结果表明,断裂伸长率 对λb对φ0、A、B、m和η的敏感性依次降低。
(4)为验证本文所建立的模型的合理性,利用所建立的本构模型参数去预测了EPDM软隔层单轴拉伸试验结果。预测结果表明,本文所建立的本构模型能够预测EPDM软隔层在大变形的失效行为以及断裂伸长率随着加载速率的增加而增加的现象,从而可为双脉冲发动机隔层打开工作过程数值仿真提供理论基础。
