考虑应变率和温度响应的少烟NEPE推进剂粘弹性本构模型

2019-07-31申依林李军强

固体火箭技术 2019年3期

申依林，任震，李军强，马松

(1. 空军驻西北地区军事代表室，西安 710065；2. 解放军95960部队，西安 710089；3. 西安近代化学研究所，西安 710065)

0 引言

少烟NEPE推进剂是一类具备低特征信号和高能量水平的固体推进剂，在精确制导战术武器中有着良好的应用前景[1-2]。国内对少烟NEPE推进剂的研制稍晚于NEPE推进剂，目前已在提高力学性能、拓宽燃速范围、降低羽烟微波衰减等关键技术上取得一定进展。作为火箭发动机的部件，少烟NEPE推进剂在生产、装配、储存过程中会受到自身重量等低应变载荷作用，且在运输、点火和起飞、高过载转弯等情况下又会受到高应变率载荷作用；此外，因为导弹武器使用的气候和地域不定，推进剂还要承受温度载荷。所以，少烟NEPE推进剂的力学性能不仅与应变有关，同时也受应变率和温度影响。而力学性能的优劣直接关乎推进剂药柱完整性及其它使用性能。因此，研究少烟NEPE推进剂在不同应变率和温度下的力学响应，建立本构模型，对于了解或分析火箭发动机在运输、储存过程中的受力情况具有重要意义。

固体推进剂的本构模型常采用基于连续介质力学的唯象学方法，如以应变不变量为参数的超弹性多项式、Mooney-Rivlin模型[3-4]、Yeoh模型[5-7]及Ogden模型[8-9]等，还包括描述粘弹性质的Maxwell模型[10]、Kelvin模型[11]、三参量固体模型[12]、Schapery模型[13]及ZWT模型[14]等。超弹性多以应变能函数与偏应变能和体积应变能的标量函数来反映，其中Mooney-Rivlin模型能较好地描述推进剂的单轴拉伸力学行为，但所得模量是常量，不适用于剪切和双轴拉伸过程，且模型的准确性与其阶次呈正相关，准确的模拟结果依赖高阶次模型，同时使计算量增大；Yeoh模型对应变能函数进行近似：忽略了Cauchy-Green张量的第二不变量I2对应变能的影响，该模型形式简便、常数项易获得并可体现反“S”形应力-应变曲线的特点，但在处理复杂应变状态时偏差较大；Ogden模型是基于主伸长比的应变能函数，其适用性较广，高阶模型可为大应变过程提供近似解，但会造成累计误差大、收敛困难等问题，因此高阶Ogden模型的应用受限。以上模型可反映推进剂应力-应变曲线的非线性特征，但在实际中推进剂变形时的应力兼具应变和率相关性，即具有粘弹特性，因此用粘弹性模型来描述更合适。在粘弹性模型中，以弹性和粘性元件形式组合成的Maxwell模型与Kelvin模型能直观地解释推进剂的粘弹性力学行为，但在阶跃载荷作用下，Maxwell模型完全松弛无应力，而Kelvin模型无瞬时响应，这与实际情况不符；三参量模型是对Maxwell模型与Kelvin模型的改进，可反映推进剂的粘性松弛特性和瞬时弹性性质，其适用性较好；Schapery模型从细观损伤和不可逆力学的角度出发，提出伪应变的概念，以伪应变与损伤变量函数的乘积来反映材料的非线性粘弹特性，该方程形式灵活，能成功用于固体推进剂；ZWT模型是非线性弹簧和两个Maxwell体的并联形式，可考虑高、低应变率对推进剂力学性能的影响，其结构简单、参数易获取，但松弛时间是非线性回归的结果，物理意义不明确。

本研究以少烟NEPE推进剂为例，在测试了应变率和温度对推进剂力学性能的影响后，建立了一种含多蠕变模式与非线性弹簧的本构模型。该模型适用于宽的应变率及温度范围，形式简单且物理意义较明确，有助于理解少烟NEPE推进剂的粘弹特性，还可为固体火箭发动机的结构设计及完整性分析提供支撑。

1 实验

1.1 推进剂制备

各组分含量见表1。

表1 少烟NEPE推进剂配方

使用5 L立式混合机进行药浆的混合，再浇注成方坯药块并在60 ℃固化7 d，按GB/T 528—1998标准制备哑铃型拉伸样条，如图1所示。

图1 哑铃形推进剂试样

1.2 性能测试

采用Instron 3300电子万能材料试验机进行单轴拉伸测试，其中拉伸速率分别为0.5、5、50、100、500 mm/min；测试温度分别为50、20、0、-20、-40 ℃，在高温或低温测试前，对推进剂试样保温1 h。在每种条件下测试5次，除去非正常断裂(从夹具处、圆弧处或缺陷处断裂)的试样，再求平均值得到推进剂在不同拉伸速率或温度下的应力-应变曲线。

2 实验结果分析

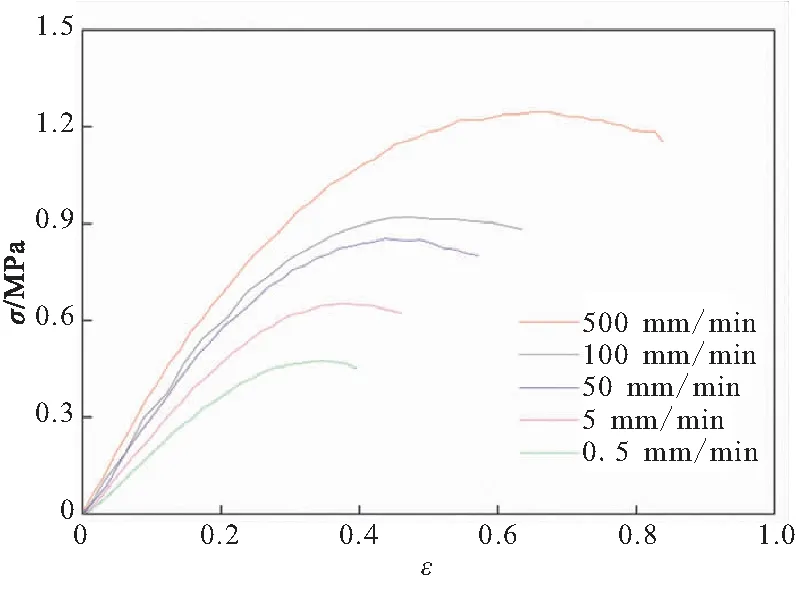
图2 不同应变率下的σ-ε曲线

图3 不同应变下的线性关系

从图2中可见，随着拉伸速率的增加，推进剂的断裂强度σb、最大强度σm、断裂延伸率εb和弹性模量(曲线初始斜率)均呈现增大的趋势，说明少烟NEPE推进剂的力学性能存在着应变率敏感特性。这是因为少烟NEPE推进剂交联网络的松弛速率较应变速率相对滞后，导致在低拉伸速率下裂纹等缺陷可充分扩展，使推进剂试样过早断裂，而在高拉伸速率下则不然。进一步分析发现，定应变条件下的应力与对数应变率呈线性关系，如图3所示，且应变越大，应力对对数应变率的变化越敏感。少烟NEPE推进剂应力与对数应变率的线性关系是下文研究力学性能率相关性的基础。

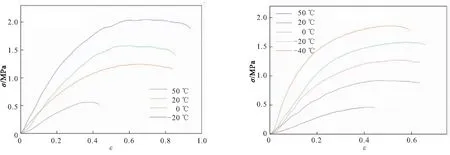
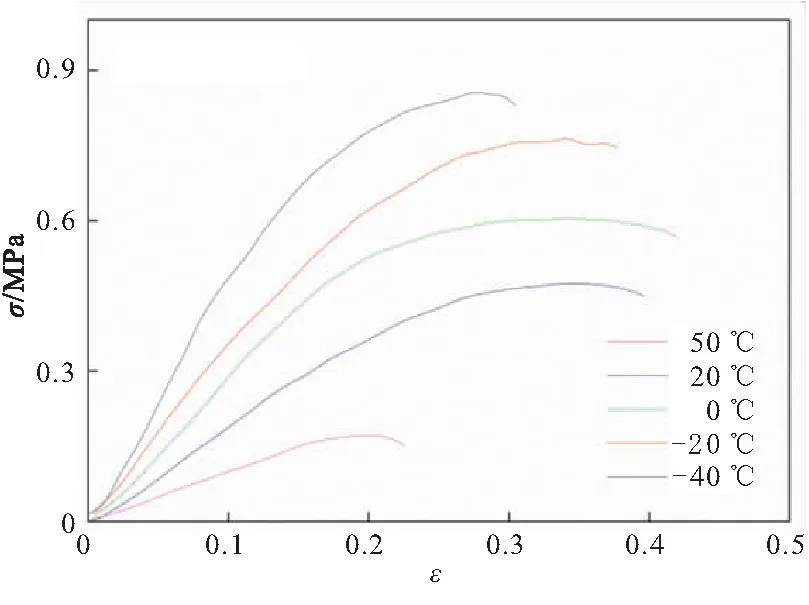
本文还研究了温度对少烟NEPE推进剂拉伸力学性能的影响。分别测试了拉伸速率为0.5～500 mm/min时，推进剂在-40、-20、0、20、50 ℃下的拉伸曲线，如图4所示。从图4可见，少烟NEPE推进剂的拉伸强度和初始模量均随着温度的下降而显著增大。当温度下降后，高分子的链刚性增强、链间内摩擦增大[15]，故其拉伸强度和模量大幅增加，但使用了PEG粘合剂的NEPE推进剂玻璃化温度较高(-38 ℃左右)，因此低温(-40 ℃)下延伸率较常温下的略小。该实验数据是下文中研究力学性能温度相关性的基础。

3 粘弹性模型的建立

为用模型反映少烟NEPE推进剂的线性对数应变率效应和温度效应，本文首先结合实验分析了常用率相关模型的特征，对其改进并建立了适用于宽应变率范围的率相关模型；再根据力学性能的温度变化特性，提出了温度函数，结合前述模型最终建立起了粘弹性本构模型。

3.1 率相关模型

为描述高分子复合材料的应变率相关性，文献[16-17]中提出了包含两个Maxwell单元的非线性粘弹性模型。在该模型中，两个Maxwell单元分别用于描述准静态和高应变率下材料的力学性能，当应变率范围不超过两个数量级时，该模型的准确性较好，具有借鉴意义；ZWT模型[14]包含两个Maxwell单元和非线性弹簧，材料在高、低应变率下的弹性和粘性响应分别由Maxwell单元的模量Ei和松弛参数，θi来反映，该模型适合描述材料在准静态和高应变率下的变形问题，其适用的应变率范围较固定，且Ei和θi是通过非线性回归得到的参数，其物理意义不明确。若使用ZWT模型来拟合也可得到数学意义上的唯象参数，但不能直观地反映线性对数应变率效应。

(a)500 mm/min (b)100 mm/min

(e)0.5 mm/min

图5 多蠕变模式与非线性弹簧并联模型

图5中的Ej和θj(j=1，2，…，n)分别为第j个Maxwell单元的弹性模量和松弛时间，Ee为非线性弹簧的弹性模量。

对于任一Maxwell单元，有

(1)

(2)

故本构方程可表示为

(3)

σe=αε+βε2+γε3

(4)

使用实验数据对式(3)进行回归，可得到各蠕变模式的Ej和θj以确定推进剂的本构方程，但直接得到各蠕变模式的松弛时间相差不大，其结果难以反映出多个蠕变模式的叠加效应，因为拟合程序无法判别各个蠕变模式的差别，导致在使用包含两个或多个蠕变模式的模型进行拟合时，其实际结果是同一种蠕变模式的多次累加。若能在拟合之前确定多个不同蠕变模式的松弛时间θj，则可通过非线性回归得到各蠕变模式的弹性模量Ej，这样一来，模型的物理意义更加明确。

(5)

图6 ε和lgθ一定时，关系曲线

考虑将多个松弛时间不同的蠕变模式进行叠加，使各松弛过程“各司其职”：对于某一特定的松弛过程，当对数应变率变化较小时，其应力与对数应变率呈线性关系，而其它松弛过程在此范围内对材料的力学响应为零或常数。这样一来，该叠加的蠕变模式可在宽应变率范围内描述材料的力学响应。为此，将图6中对数应变率差值为2的曲线①、曲线②、曲线④和曲线⑧进行叠加，得到图7中的曲线①；将图6中对数应变率差值为1的曲线③、曲线④、曲线⑥和曲线⑧进行叠加，得到图7中的曲线②；图6中对数应变率差值为0.5的曲线⑤、曲线⑥、曲线⑦和曲线⑧进行叠加，得到图7中的曲线③，如图7所示。

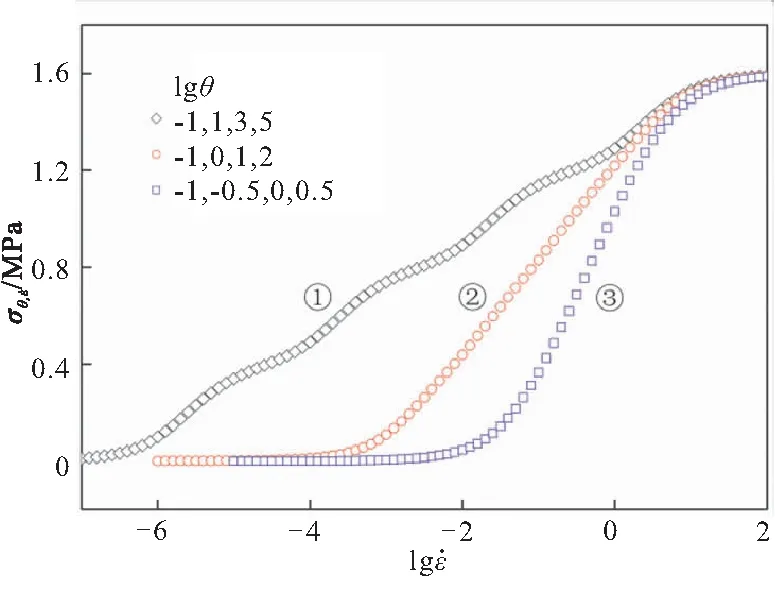
图7 多个蠕变模式的叠加

(6)

进而可得：

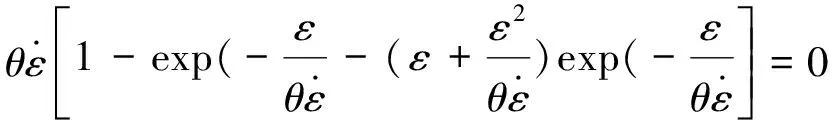
(7)

根据式(7)求得某一确定应变下(为保证在高应力区的拟合精度，本研究取0.4)，松弛时间与应力-对数应变率曲线上斜率最大点处(Pmax)应变率的关系，见图8。

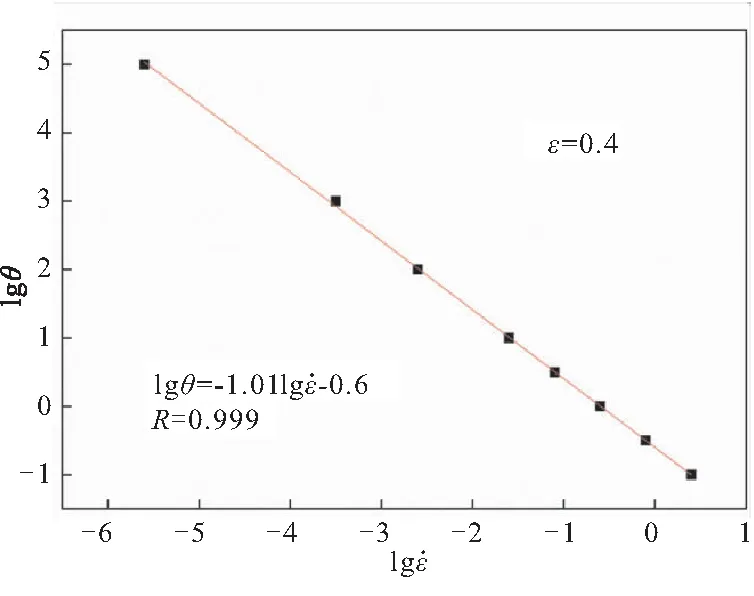
图8 lgθ与曲线上斜率最大点处的关系

(8)

表2 对数应变率和所对应的松弛时间θ

由表2可见，与各对数应变率对应的松弛时间从0.61 s增至651.65 s，共跨越了4个数量级，考虑使用对数松弛时间为1的5个蠕变模式(θ分别为0.1、1、10、100、1000 s)进行叠加，以构成少烟NEPE推进剂的粘弹性本构模型，当拉伸速率在0.5～500 mm/min之间变化时，可用5个蠕变模式的线性组合来反映推进剂的力学响应。需说明的是，式(3)中使用多项式σe是为了表征推进剂的非线性弹性性质，经拟合后发现，三次多项式的效果较理想，σe的展开形式为αε+βε2+γε3。

将松弛时间以及各拉伸速率下的实测数据代入计算程序中进行多元非线性回归，可得到模型中各参数的数值，其中非线性弹性部分的参数α、β和γ分别为1.971、-3.194和0.554；各蠕变模式的弹性模量及松弛时间见表3。

综上可得少烟NEPE推进剂单轴拉伸的粘弹性本构方程：

(9)

σe=1.971ε-3.194ε2+0.554ε3

(10)

3.2 温度函数模型

在用模型反映推进剂力学性能的温度相关性时，既有直接加入温度项的方式[18]，也有采用率温等效理论的方法[19]，而后者需应变率与温度能相互关联，一般在模型上较难实现。本研究采用较直观、有效地方法：在率相关模型的基础上引入温度函数项，来反映温度对力学性能的影响，再根据不同温度下的测试数据回归出温度函数中相关参数，最终建立起考虑应变率和温度响应的本构模型。

假设有温度函数g(T)，加载过程的应力为g(T)与率相关模型的乘积形式：

(11)

对于式(11)中的g(T)，分别使用过幂硬化函数和线性温度函数，最终发现后者的拟合效果较好且又便于数据处理，因此本节使用线性函数来表示g(T)：

(12)

式中α为温度因子，该参数可通过影响温度函数从而决定应力应变曲线的形状，α在给定应变率下并非常数，而是T/T0的多项式形式。

值的说明的是，温度函数g(T)中的参考温度T0为20℃，其他温度下的应力值均是20℃的应力应变曲线与温度函数的乘积。

将式(9)代入式(11)，可得少烟NEPE推进剂的率和温度相关模型，再通过不同温度下的实验数据对该模型进行多元非线性回归，得到α的表达式：

(13)

温度函数g(T)的展开式：

(14)

归并式(9)和式(14)，最终得到少烟NEPE推进剂本构模型的展开式：

(15)

4 模型的实验验证

为验证少烟NEPE推进剂粘弹性模型的准确性，使用式(15)分别对不同拉伸速率和温度下推进剂的应力-应变曲线进行预测，与实验结果做了对比，如图9所示，其中(a)～(e)是实验和模拟曲线的比较，(f)和(g)是拟合结果偏离实测数据的百分误差，百分误差E%=|(ν-νfit)/ν|×100%，其中ν为实验数据，νfit为拟合数据，E%反映了拟合值偏离实验值的百分比率，以此反映该模型拟合效果的好坏。

(a)σ-ε,0.5 mm/min (b)σ-ε,5 mm/min

(c)σ-ε,50 mm/min (d)σ-ε,100 mm/min

(e)σ-ε,500 mm/min

(f)百分误差,0.5、5、50 mm/min (g)百分误差,100、500 mm/min

从图9可见，实测和预测曲线符合地较好：在应变为0.1～1.0的范围内，拟合百分误差小于24%，而当应变小于0.1时，拟合误差较大。这可能是由于为保证初始时刻的应力为0，在实验的初始时刻，推进剂试样在夹具内未完全固定至产生张力，在载荷作用下，试样与夹具产生一定的滑移，而此时的测试值ν较小，导致百分误差偏大。

总体而言，在较大的应变范围内，模型的拟合效果较理想，说明多蠕变模式与非线性弹簧的并联模型，以及率相关模型与温度函数的乘积形式较适合描述少烟NEPE推进剂力学性能的应变率与温度相关性。该模型有助于更好地理解推进剂的力学行为，还可为本构模型的发展提供思路。