响应面分析法优化聚丙烯无纺布抗静电接枝工艺

2019-07-30王晓旭魏春艳

印染助剂 2019年6期

关键词：抗静电响应值无纺布

苗苗，刘超，王晓旭，王迎，魏春艳

（1.大连工业大学纺织与材料工程学院，辽宁大连 116034；2.大连工业大学信息科学与工程学院，辽宁大连 116034）

聚丙烯（PP）无纺布对人体无毒副作用，广泛应用在纺织和医疗卫生等领域［1-3］。PP 分子不含亲水性基团且结晶度高，易产生静电且难以逸散［4-5］，会造成火灾甚至爆炸等危害。因此，对PP 无纺布进行抗静电改性十分必要。

本实验采用响应面分析法对紫外光辐射接枝PP无纺布的工艺进行分析和预测。以摩擦电压为响应值，分析接枝单体质量分数、光引发剂浓度和紫外光照时间对摩擦电压的影响，确定最优工艺并验证该优化算法的可行性。

1 实验

1.1 材料与仪器

PP 无纺布（25 g/m2，大连瑞光无纺布集团有限公司），丙烯酸（AA，化学纯，天津市光复晶系化工研究所），二苯甲酮（分析纯，天津市大茂化学试剂厂），无水乙醇（分析纯，天津市光复科技发展有限公司），去离子水（实验室自制）。PTT-A+200 电子天平（福州华志科学仪器有限公司），702-6 电热恒温鼓风干燥箱（大连实验设备厂），UVA CUBE 100 紫外光固化箱（Honle UV Technology 公司），织物摩擦式静电测试仪（莱州市电子仪器有限公司）。

1.2 实验方法

用无水乙醇浸泡PP 无纺布并超声清洗30 min，去除生产、运输过程中的杂质和油污，80 ℃烘干至恒重，冷却并测量摩擦电压。在避光处将丙烯酸和二苯甲酮配制成溶液，将PP 无纺布浸泡其中一定时间，并在UV 灯下固化。取出后用去离子水清洗，80 ℃烘干至恒重，冷却并测量摩擦电压。

1.3 测试

试样准备：将丙纶无纺布放入50 ℃烘箱中烘干，随机取80 mm×40 mm 的试样16 块，在（20±2）℃、相对湿度（35±5）%的环境下放置24 h，不得污损。织物等级要求如表1所示。

表1 摩擦带电电压技术要求

抗静电性能：GB/T 12703.5—2010《纺织品静电性能的评定第5部分：摩擦带电电压》［6］进行测试。

1.4 响应面实验

运用Box-Behnken 设计原理，选取A丙烯酸质量分数5%～15%，B光引发剂浓度0.04～0.06 mol/L，C紫外光照时间15～25 min 为实验因素，每个因素选取3个水平，编码公式如下：

由编码公式可知，当A=5、10、15 时，X1=-1、0、1；同理，当B=0.04、0.05、0.06 时，X2=-1、0、1；当C=15、20、25时，X3=-1、0、1。本实验各因素水平如表2所示。

表2 实验因素水平

2 结果与讨论

2.1 响应面建模及实验结果

根据Box-Behnken 软件设计了3 因素3 水平共17组实验，以摩擦电压（Y）为响应值，其中5 次中心点实验用于估计实验误差。实验设计方案和结果见表3。

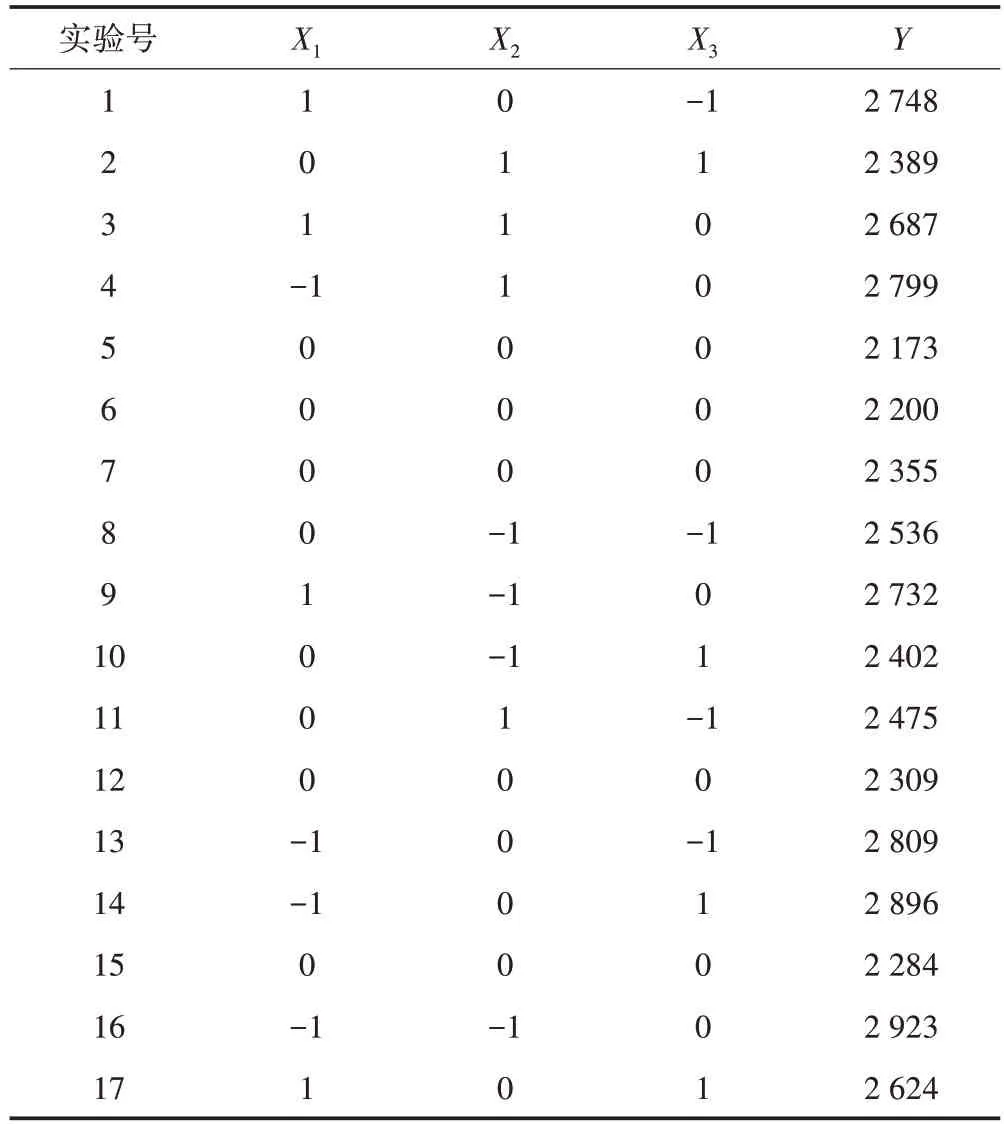
表3 实验设计方案和结果表

2.2 模型回归分析

利用Design-Expert V8.0.6 软件对实验数据进行多元回归分析，建立二次多项式回归方程Y=2 264.20-79.50X1-30.38X2-32.13X3+19.75X1X2-52.75X1X3+12.00X2X3+419.90X12+101.15X22+85.15X32。式中：正项系数代表该因素值增加会增大响应值，负项系数代表该因素值增加会降低响应值。

2.3 模型方差分析

从表4 可知：（1）模型F值（25.68）足够大，P值小于0.000 1，表明模型回归显著，预测公式可以准确反映变量与响应值之间的关系。（2）失拟项P=0.816 1，表示回归方程的失拟项检验不显著，说明未知因素对实验结果干扰很小，拟合检验显著，该方程的拟合度良好，能较好地反映丙烯酸质量分数、光引发剂浓度、光照时间与摩擦电压的关系，因此所得回归方程能较好地预测摩擦电压随参数的变化规律。（3）丙烯酸质量分数（X1）P=0.009 7 小于 0.05，对摩擦电压影响显著；X1X2、X1X3、X2X3的P值均较大，说明两两因素的交互作用相对较小；的P值均小于 0.05，说明实验因子与影响值不是呈单一的线性关系。（4）本回归模型R2=0.970 6，实测值与预测值相关性较高，说明用该模型对摩擦电压进行分析和预测合理。

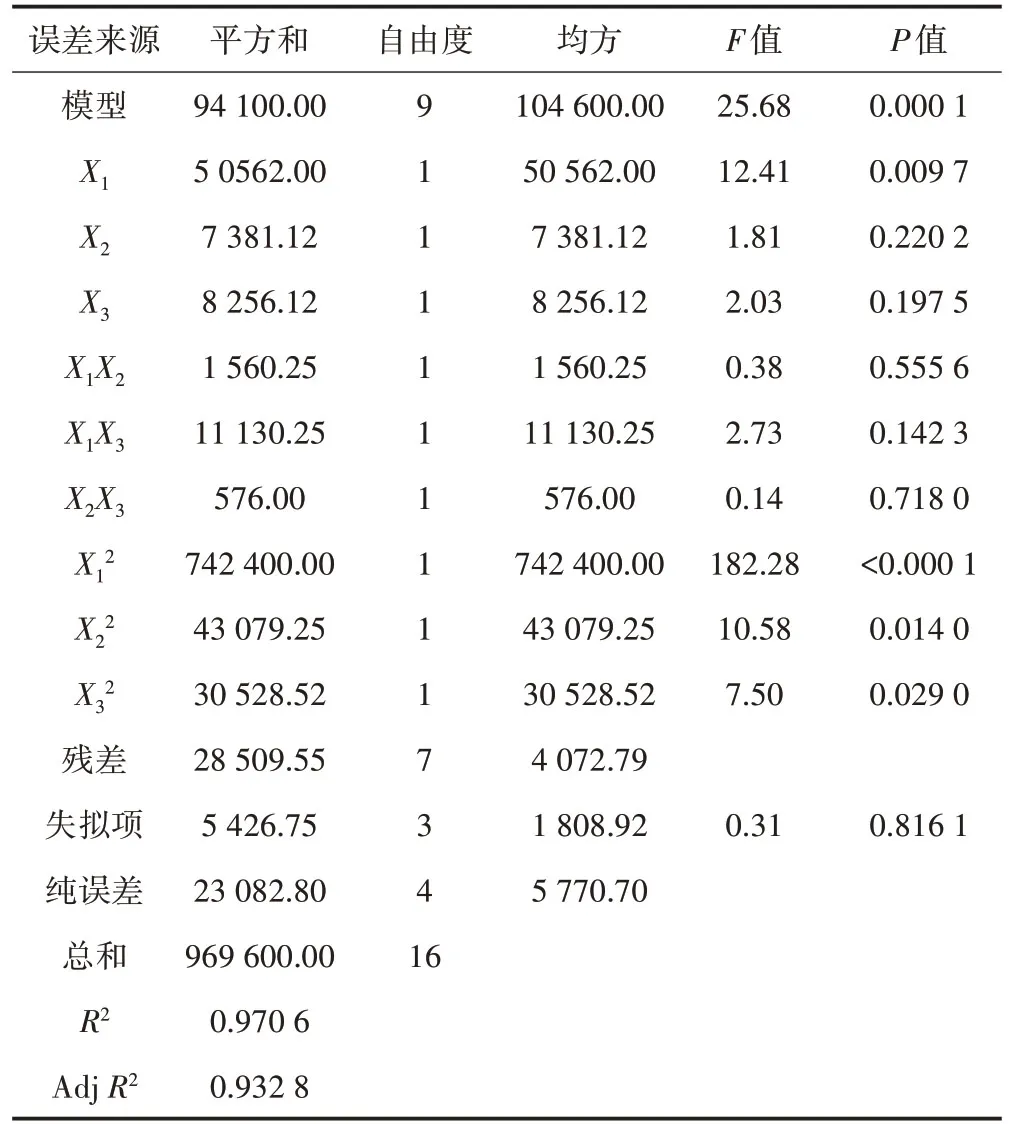
表4 方差分析表

将编码公式带入二次多项式回归方程，可得摩擦电压关于实验因素A、B、C的二次多项式回归方程Y=16.80A2+1 011 500.00B2+3.41C2+395.00AB-2.11AC+240.00BC-329.37A-1 129.38B-133.57C+8 289.87。

2.4 模型残差分析

从图1 可知，响应值基本都附着在残差线上，说明模型符合正态分布。

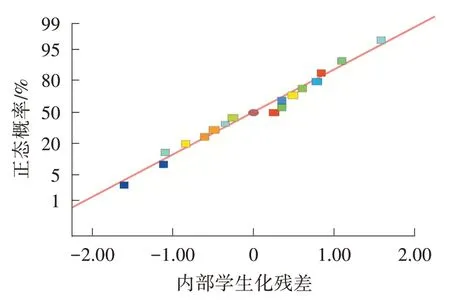
图1 正态概率分布图

从图2、图3 可看出，内部、外部学生化残差均分布在±3 内，说明不存在非正常数据，无隐藏的影响响应值的因素，且数据点随机分布，没有任何趋势和异常数据点，进一步说明模型可靠。因此响应面多项式模型能够有效地模拟各个变量对摩擦电压的影响。

图2 内部学生化残差分布图

图3 外部学生化残差分布图

2.5 响应面分析

从图4 等高线的陡缓程度可以得出影响摩擦电压的主次因素：单体质量分数、光照时间、光引发剂浓度，与方差分析结果一致；时间与光引发剂浓度的交互作用显著。

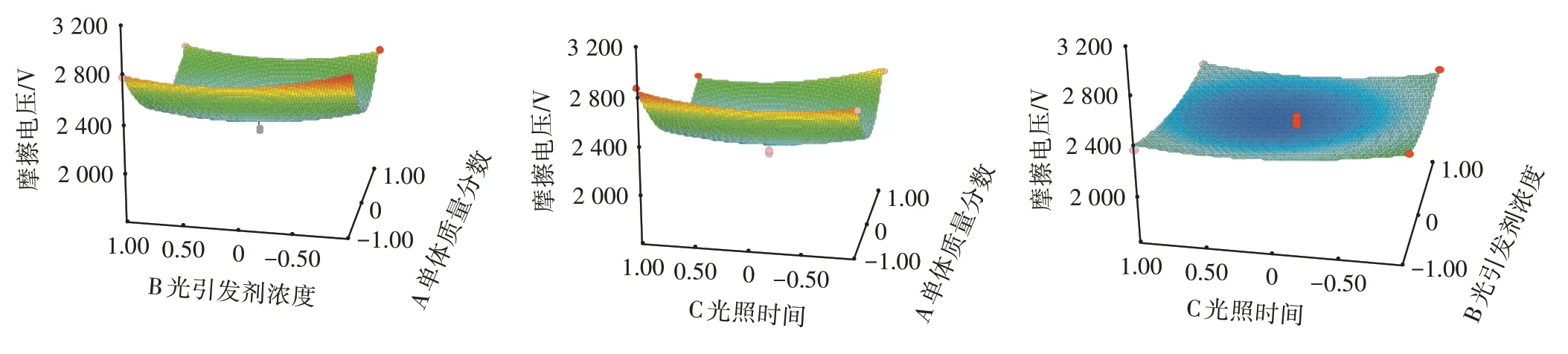
图4 响应曲面图和等高线图

2.6 模型优化

通过响应面分析方法，再结合响应面模型，模拟出抗静电接枝改性的优化工艺：单体质量分数为10.48%，光引发剂浓度为0.051 mol/L，光照20.69 min，预测优化工艺条件下的摩擦电压Y为2 255.16 V。如图5 所示，实际值与预测值是十分接近的，基本在一条直线上。

图5 实际值与预测值比较图

实验验证此优化工艺，结果如图6 所示。原PP 无纺布的摩擦电压为2 869～3 122 V，改性后的PP-AA摩擦电压为2 200～2 475 V（明显变小），改性后PP 无纺布达到了C 级摩擦带电电压技术要求。说明响应面模型具有一定的可信度，能够有效地预测实验各因素对摩擦电压的影响。

图6 改性前后PP 摩擦电压图

2.7 各因素对实验结果的影响

由图7 可知，随着单体质量分数的增加，摩擦电压先减小后略微增大。这是因为单体质量分数增加，自由基反应增多，接枝率增大，PP 无纺布表面亲水基团增多，抗静电性增强，摩擦电压减小；当单体质量分数达到10.48%后继续增加时，单体之间发生均聚反应的概率增大，接枝率降低，导致抗静电性降低，摩擦电压增大［7］。随着光引发剂浓度的增加，产生的自由基增多，接枝率增大，PP 无纺布表面亲水基团增多，抗静电性增强，摩擦电压减小；当光引发剂浓度达到0.051 mol/L 后，继续增大浓度，自由基之间相互反应的概率增大，使反应提前终止，造成PP 无纺布的抗静电性降低，摩擦电压增大。光照时间对实验结果的影响与光引发剂浓度的影响类似。