一种船舶充液管路声振耦合工程计算方法
2019-07-30吴江海尹志勇孙凌寒孙玉东
吴江海,尹志勇,孙凌寒,孙玉东
(中国船舶科学研究中心 船舶振动噪声重点实验室,江苏 无锡214082)
0 引 言
充液管路广泛地应用于舰船、海洋工程和石油能源等装置中,管路系统中存在的泵、阀门等内部声源以力激励和声激励两种方式诱发管道产生振动噪声,并在管道和流体中传播。振动噪声问题在舰船管路系统中,显得十分突出,一方面会造成管路以及精密仪器附件破坏,影响管路系统以及动力系统的正常运行;另一方面管路系统的振动噪声会通过船体以及管内介质传播引起水下声辐射,影响舰船的隐身性能,对其安全构成威胁[1]。
管内介质中的声波与管路结构振动相互耦合引起管路振动噪声,因此人们对管道中声波传播的模态,各种耦合机制的影响进行了研究,提出了各种充液管系声-弹耦合振动模型。声弹耦合模型考虑了流体在轴向的可压缩性(压力脉动)而没有考虑其横向的压缩性。这是由于对一般的长径比较大(L/D)≫1的管道共振时脉动压力的波长远大于管径,因此在管道横向振动时就可以忽略流体压缩性的影响[2]。
Fuller和Fahy[3]首次将弹性薄壁方程与三维声波导方程完全耦合,考虑泊松效应,建立充液圆管中波传播的频散方程和能量流分布的理论公式,给出了钢管、橡胶管和不同壁厚/半径比下轴向波的计算结果。Sinha和Plona等人[4-5]针对受内部流体载荷、外部流体载荷和内外同时作用载荷三种情况下任意厚度圆柱壳,给出了轴对称声波传播的理论和试验研究结果。Brevart等人[6]在Kennard壳体方程与管内介质声传播方程耦合研究的基础上,通过施加径向力进行了波的主动控制。Junger[7]采用刚度-阻尼模型研究了柔性层对考虑外部声介质载荷作用下的圆柱壳振动影响。本文首先建立管路系统声振耦合方程,采用阻抗综合法求解管路系统声激励下管系振动响应,并开展相关仿真与试验验证。
1 理 论
泊松耦合与连接耦合是振动与噪声沿管路传播时存在的重要的耦合方式,阻抗-导纳综合法基于充液管路十四方程理论,以管路系统六自由度位移与管内声压为变量,该方程中包含了振动源与噪声源,泊松耦合通过管路单元阻抗矩阵中的耦合阻抗加以考虑,连接耦合则在弯头和分支管道处,考虑声压与管道内力之间的相互作用。在阻抗-导纳综合法中,图1中的弯头在节点j处有管壁速度和流体连续条件,用矩阵形式表示如下:



图1管路弯头与分支Fig.1 Bend and branch
在节点j两端的单元,完整的阻抗矩阵应满足下式:

其中:cij,dij是结构与声的耦合阻抗;aij是声阻抗。利用该式将(2)式中的节点力用节点速度表示,然后与(1)式一起写成矩阵形式如下:

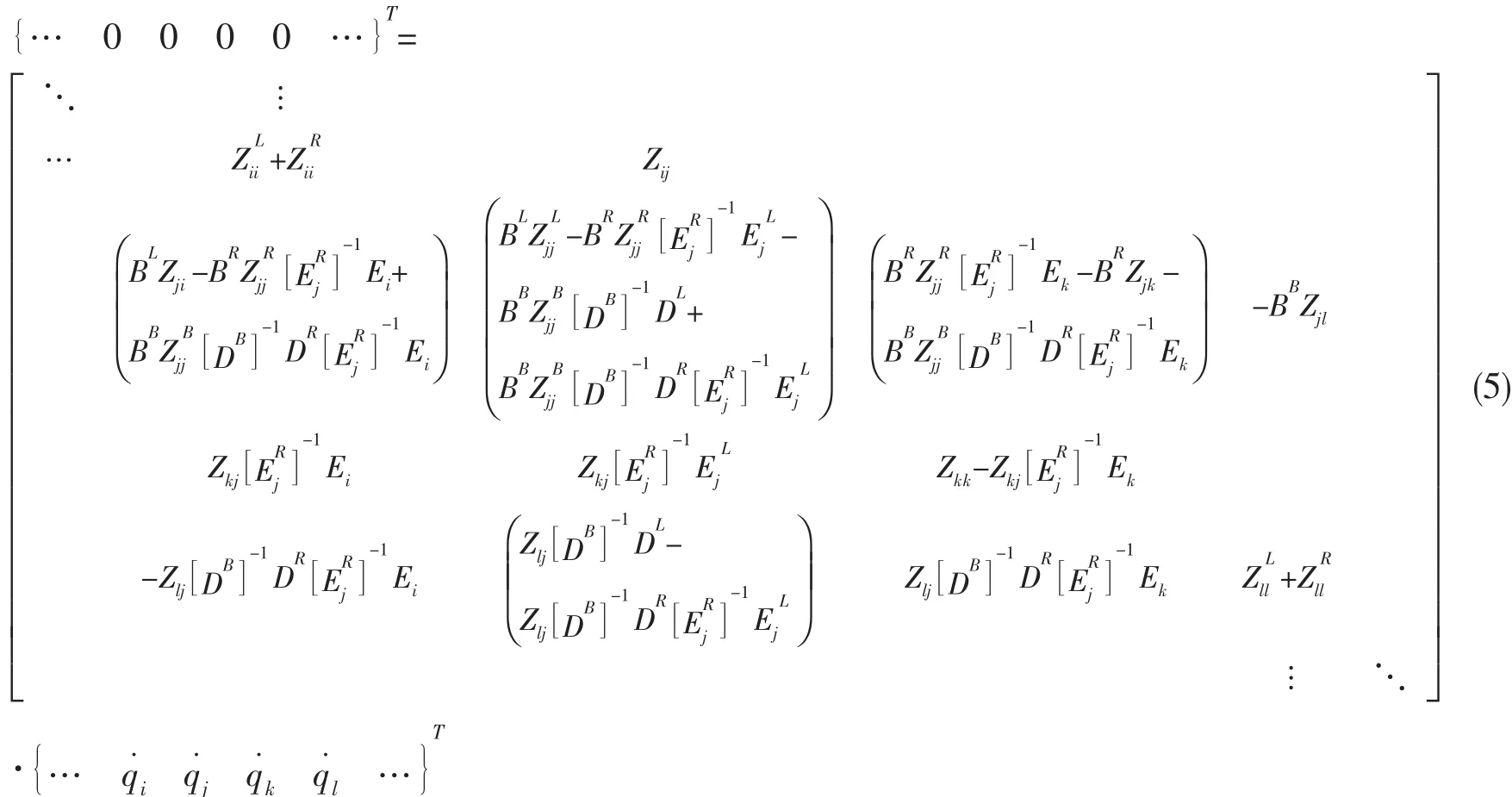
管路中存在着流固、声振和流声三种耦合,流固耦合主要由流体的湍流脉动压力产生。要直接通过计算流体考虑管路系统流固耦合作用,代价太大,也没有必要,即使只考虑流体对管壁的激励作用,计算量也不小。因此,将流体对直管、弯头、分支等部位的激励简化为分布力或集中力[8],应用试验方法测量这些力,然后将测量结果直接代入(4)式或(5)式左端的源向量中即可计算管道响应。
2 有限元仿真结果
为考虑管内声波与管壁之间的泊松耦合与连接耦合,设计如图2所示的三维空间计算管路模型。该模型由三段直管、两端弯管以及端盖组成,直管长度为1 m,弯管曲率半径为0.2 m。管路系统共标为6个节点,其中2、5节点为边界支撑条件,在节点1处施加单位声压激励。管路外径为80 mm,管壁为5 mm,采用本文的阻抗矩阵法与有限元分别建立计算模型,有限元模型中管壁采用shell单元,密度为7 800 kg/m3,杨氏模量为2.1E11,网格数量为8 400,管内流体采用声单元模型,密度为1 000 kg/m3,速度为1 500 m/s,网格数量为3 250。
首先对管中的声压传递进行验证,对比2、5节点处声压,参考声压为1e-6 Pa。从对比图3中看出,本文计算结果与有限元计算结果幅值大小与峰值个数保持一致,这是由管路系统本身的结构外形所决定。两者在第一个峰值处频率产生了相位差,有限元计算的第一阶声压峰值对应频率偏大,200 Hz以后,两者吻合度较好。

图2有限元计算模型Fig.2 Finite element model

图3声压计算对比Fig.3 Comparison of sound pressure
管壁上测点三向振动加速度对比如图4所示。由图中可以看出,虽然管路的激励只是沿着进口处的轴向施加,但是管壁上测点三向振动加速度的量级相差不大,这是由于在两处弯管处发生了连接耦合与泊松耦合响应,本文的计算方法与有限元计算中的峰值大小,振动加速度峰值以及加速度变化趋势保持一致。因此可采用本文计算方法对舰船管路中因水泵噪声源等激励管路产生的振动进行工程预报。


图4管壁测点振动计算对比Fig.4 Comparison of pipe wall vibration
管路系统振动沿支撑传递到船体引起船体振动进而诱发船体水下辐射噪声是管路系统振动计算中的重要传递途径。因此管路系统振动通过支撑引起船体的振动也是管路振动预报的重要对象,管路船体连接处的振动大小由该处船体输入阻抗与管壁上的振动响应以及管路支撑隔振效果三者确定。本文计算中假设管路支撑为弹簧支撑,船体结构阻抗可以通过有限元或者试验测试方法获取,这也是本文计算方法优于传统有限元计算的优点,即不需要将整个船体及管路系统的有限元模型建立。本文工程计算的另一优点即振动响应预报的频率范围由船体阻抗频率范围决定,采用试验测试阻抗值优于传统有限元计算因网格数量而受到的计算频率上限限制。
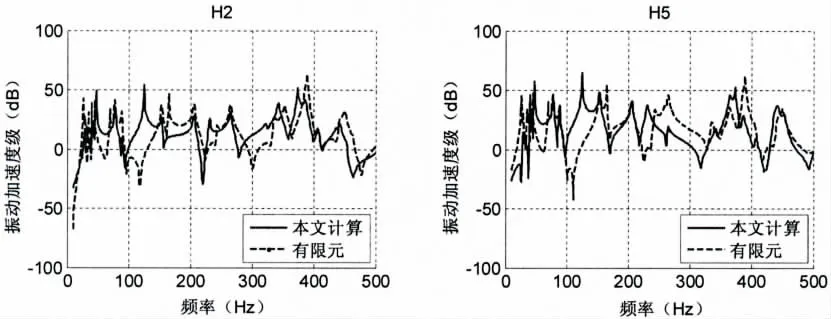
图5基础测点振动计算对比Fig.5 Comparison of basic vibration
从图5可以看出,船体上振动响应要小于管壁上三向振动加速度,弹簧支撑具有较好的隔振效果。本文计算的船体振动与有限元计算结果幅值与趋势保持一致,200 Hz以后,两者曲线几乎重叠,说明本文对于船体振动的预报具有较高的精度。
3 试验结果
试验对象为弹性支撑状态下的充水管路,由DN80直管、弯头和三通管组成,端部用法兰盖密封。其中一个端部用法兰盘式活塞声激励装置密封(见图6)。可用该装置对管路进行声激励。管路形状为空间结构,管路在4个点用弹性支撑支撑。其中3个弹性支撑安装在680 mm×520 mm×10 mm的平板上。另一个安装在高约1 m的基座上。平板和基座用螺栓连接于实验室地面T形槽上。在0.4 MPa压力下用激振机激励安装在管道端部的活塞声激励装置,测量活塞上加速度、管道内部流体介质的声压、管路若干点的加速度。

图6管路与测点布置图Fig.6 Piping and measuring point layout
图6所示为管道与测点的布置图。激振机在沿y轴激励活塞盘,测量A1~A3点在xyz轴方向的加速度响应和P1~P6点的声压。除此之外,在声激励装置的活塞盘上还安装一个单向加速度计(A1)。图7为声激励装置安装示意图。
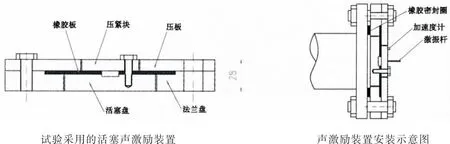
图7声激励装置Fig.7 Acoustic excitation device
3.1 声激励下声压值对比
图8为0.4 MPa声激励下六个测试点声压测试值与计算值的对比情况。从图中可以看出,计算的管内声压与试验测试声压基本吻合,说明本文的计算方法具有较宽的计算频率和精度。


图8计算与试验测试声压对比Fig.8 Comparison between calculation and test of sound pressure
3.2 声激励下加速度值对比
图9-10为0.4 MPa声激励下加速度测试点A1-A3点三向加速度频响曲线计算值与试验值的对比曲线图,计算结果与实验结果吻合程度较好,这证明了本文所用的计算方法和计算程序的有效性。此外,由对比结果可见,距离声激励点近的A1点加速度测量值与试验值的吻合程度比A2和A3要好。本文的计算方法与试验测试结果虽存在一定误差,但均在工程误差允许范围内。
离激励点较近处:离激励点较远处:

图9 A1处计算与试验测试振动对比Fig.9 Comparison between calculation and test of vibration A1
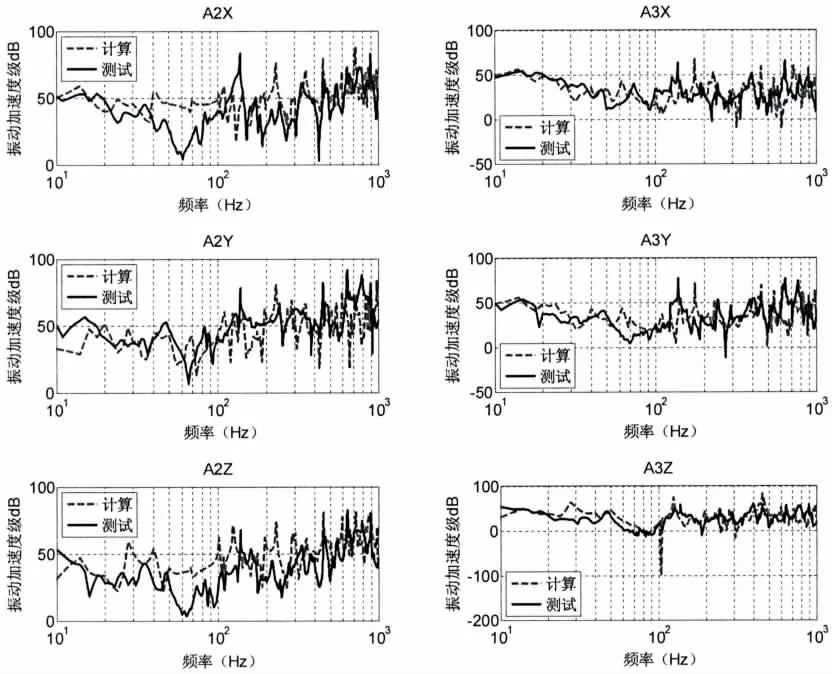
图10 A2/A3处计算与试验测试振动对比Fig.10 Comparison between calculation and test of vibration A2/A3
4 结 论
本文基于阻抗导纳法建立充液管路声振耦合工程计算方法。该方法基于管路元件的阻抗导纳矩阵,以各管路元件作为子系统,以各子系统连接节点处的位移与管内声压连续作为边界条件。针对该方法进行了有限元计算与试验测试验证。
有限元计算验证表明:文中的计算方法对管内流体中声压、管壁的振动以及船体上的振动具有较高的吻合度,在低频段,计算结果峰值幅值一致,但在频率上存在差异,这是由于计算中基于的理想状态下的边界连续条件与有限元中的边界条件存在差异;
试验测试验证表明:本文的计算方法具有优于有限元的较宽的计算频率范围,针对复杂的空间管路,文中计算的管内声压与管壁上振动计算与试验结果吻合较好,说明该计算方法具有较高的正确性与工程应用价值。
