考虑非对称剖面中和轴偏转的改进Smith法研究

2019-07-30李陈峰马开开张旭辉周学谦

船舶力学 2019年7期

李陈峰，高超，马开开，张旭辉，周学谦

（哈尔滨工程大学船舶工程学院，哈尔滨 150001）

0 引言

极限强度和剩余强度评估是船体结构设计非常重要的两个方面，其中极限弯矩（承载能力）计算是其中重要的工作之一。目前，极限弯矩计算方法除了类似始屈弯矩法这类基于剖面应力分布假定的解析法外，最常用的是逐步破坏法。逐步破坏分析方法又分为简化逐步破坏法（Smith法）[1]、非线性有限元法[2]和理想结构单元法[3]等。相比于非线性有限元法和理想结构单元法，Smith法通过离散剖面结合曲率增加和单元应力的确定，计算船体弯矩-曲率曲线来确定极限弯矩，使用方便，且计算效率和计算精度较高，在船体初步设计阶段被广泛采用。2014年IACS发布的《Common Structural Rules for Bulk Carriers and Oil Tankers》（HCSR）[4]，将其作为船体梁极限弯矩计算主要方法之一，并对计算流程作出了明确规定。

Smith法的计算精度很大程度上取决于两个方面：单元应力-应变关系的计算精度和剖面瞬时中和轴的计算精度。对于单元的应力-应变关系，已有很多学者提出了确定的方法，HCSR也详细给出了不同失效模式下单元应力-应变关系的简化计算方法。对于中和轴位置的确定，在HCSR规范[4]给出的Smith法中，中和轴位置的确定通过中和轴上下部分拉压力平衡准则来确定。该方法可以有效解决完整船剖面中和轴位置确定的问题，但是当船体发生横倾或者破损时，剖面中和轴不仅会发生平移还会有一定的偏转，所以Choung等人[5]给出了另一准则-力矢量平衡准则。这两个平衡准则对于中和轴的确定提供了可靠的理论方法，但是在实际应用求解过程中，需要采用一定的数值技术来使力平衡准则及力矢量平衡准则达到预期的收敛精度。李陈峰等[6]提出采用线性搜索法追踪中和轴位置，求解过程中以力平衡误差值和力矢量平衡误差值作为判断准则，在给定的一系列解中选取一个最优解作为瞬时中和轴的位置。这种求解方法考虑了中和轴的偏转，虽然将中和轴的平移和偏转作为两个问题分开求解，与中和轴的实际移动情况不符，但是其计算结果达到了较高的精度。

剖面瞬时中和轴的求解，实际上是一个在给定空间内寻求群体最优解的过程，Kennedy和Eberhart[7]提出的粒子群优化算法（Particle Swarm Optimization，PSO）可以很好地解决这一问题。PSO是一种智能优化算法，这种优化算法受到鸟群社会行为的启发，群体中每个粒子都能够从临近的粒子和历史经验中获得有利信息。在迭代过程中，每个粒子都会在个体最优解与群体最优解的“指导”下更新粒子的位置和速度，粒子搜索范围将很快缩小，并以最快的趋势趋向问题空间内的最优解。将这种搜索方式用于Smith法追踪中和轴位置，可以同时考虑中和轴的平移和偏转，并以非线性迭代的方式更快地靠拢群体最优解。

本文在考虑力平衡准则和力矢量平衡准则的基础上，结合多目标粒子群优化算法（Multi-Objective Particle Swarm Optimization，MOPSO）研究建立了一种非对称剖面中和轴确定方法，并在此基础上改进了现有的Smith法，以实现非对称剖面的极限承载能力分析。通过对Dow1/3护卫舰试验模型[8]完整正浮工况和多个破损横倾工况的极限弯矩计算，证明了对于受损船舶，中和轴偏转对剖面弯矩有显著影响，且基于MOPSO的中和轴确定方法具有较好的自适应和计算精度。

1 Smith法基本原理及中和轴收敛准则分析

1.1 Smith法基本原理

Smith法通过荷载增量迭代来反映剖面构件破坏的实际过程，对每一增量步，根据平断面假设以及船体剖面的瞬时中和轴计算得到剖面上每一单元的应变，由单元的应力-应变关系可进一步得到单元的应力。剖面所有单元的应力对瞬时中和轴取矩，得到的总和即为对应增量步的剖面弯矩。逐步增加曲率，得到弯矩-曲率曲线，曲线斜率为零或为负点所对应的弯矩值即为舰船的极限弯矩。

HCSR规范中，Smith法的标准计算流程如图1所示。其中，Ni代表中和轴的瞬时位置，χi代表每一迭代步的瞬时曲率值，Δχ代表曲率增量，χF代表终止曲率，F代表剖面总合力，Mi代表每一迭代步的船体梁弯矩。

1.2 非对称剖面中和轴收敛准则

对于剖面中和轴的确定，HCSR规范中考虑剖面的力平衡，中和轴上下拉压力合力为零，如图2所示，给出的收敛准则如下式：

其中：Fc为剖面所有单元压力的合力，Ft为剖面所有单元拉力的合力，ξT为力平衡误差值，一般取小于0.01。

HCSR规范提出的力平衡准则只适用于船体横剖面为对称剖面的情况，但是当船体剖面为非对称剖面时，其受力情况如图2所示。根据Choung等人[5]对于非对称剖面状态下中和轴移动情况的研究，为保证剖面的拉压力平衡，此时中和轴将会同时发生偏转和平移，此时要确定中和轴的位置除满足力平衡准则外，还需要满足力矢量平衡准则：

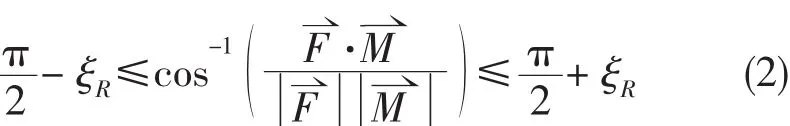
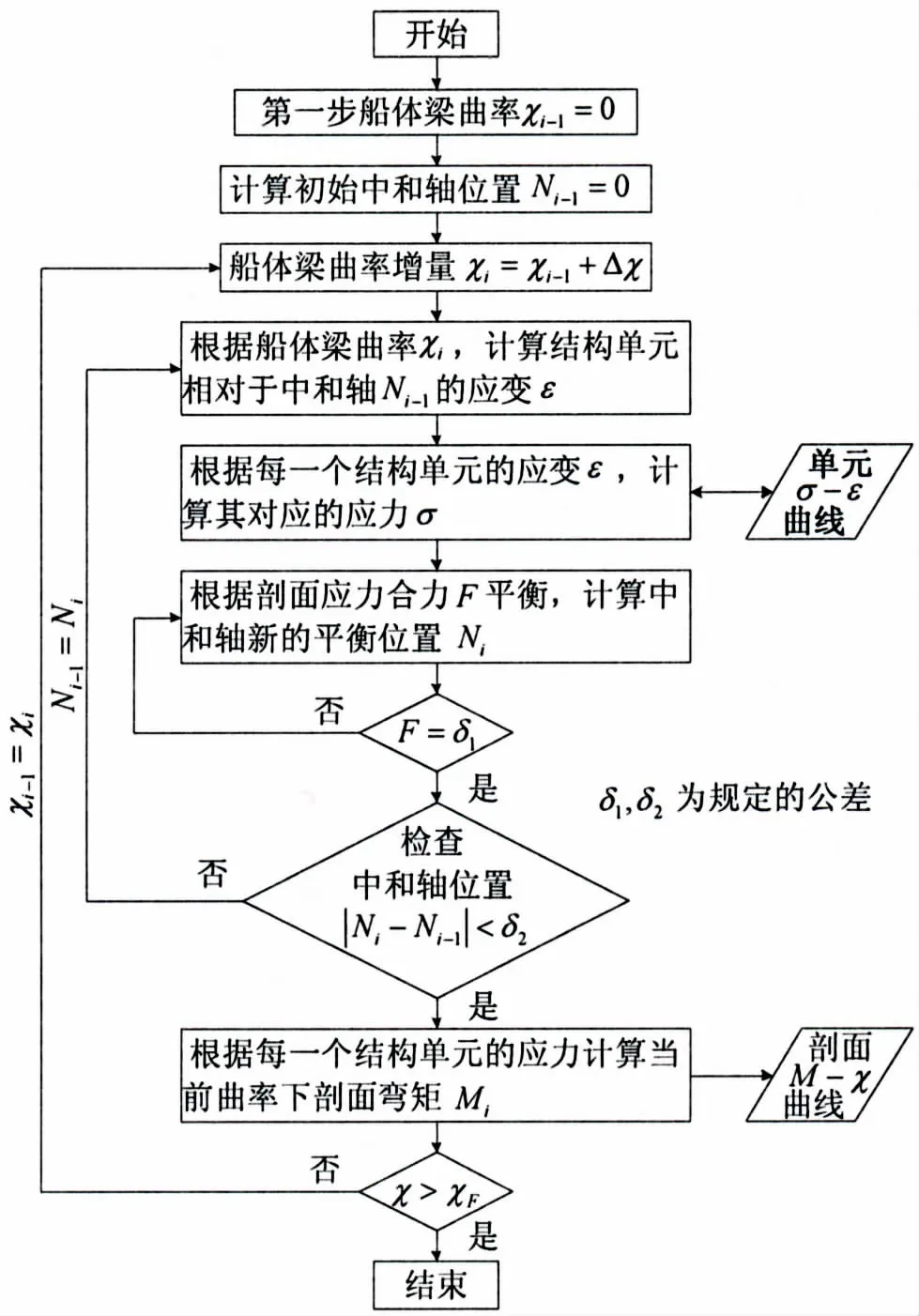
图1 Smith法基本流程图[4] Fig.1 Flow chart of procedure of Smith’s method[4]

理论上，根据上述给出的力平衡准则和力矢量平衡准则，可以确定任意剖面的中和轴位置，但要同时满足两个收敛准则需要一定的数值技术。

2 基于粒子群算法的中和轴确定方法及其在Smith法中的应用

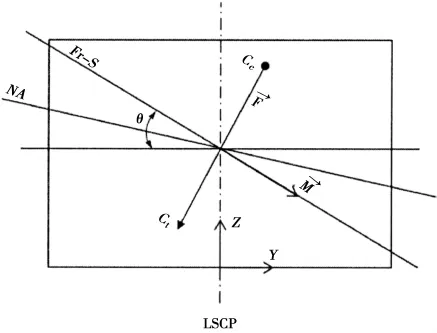
图2非对称剖面受力情况Fig.2 Force condition under asymmetric hull cross-section

非对称剖面中和轴的求解，实际上是一个在给定空间内寻求群体最优解的过程。粒子群算法是一种基于随机智能搜索的迭代方法，在搜索过程中，对于中和轴既发生平移又发生偏转的情况，粒子群算法可将平移和偏转作为粒子的两个维度，通过目标函数的建立搜索中和轴位置，实现中和轴同时平移和偏转；粒子的搜索空间及粒子的移动均具有随机性，可以实现中和轴的非线性迭代，扩大搜索空间；并且随着迭代的不断进行，粒子群算法会考虑粒子之间的相互作用，带着随机扰动不断更新粒子的最优位置，可以提高中和轴计算的精度。因此，本文考虑将PSO用于非对称剖面中和轴的确定，将其应用于改进现有的Smith法。

2.1 多目标粒子群算法基本原理

PSO的优化过程为初始化产生N个粒子，每个粒子对应优化问题的一个解，解中包含的变量个数即为粒子的维度，粒子i用d维向量xi和vi表示其位置和速度。粒子不断更新自己的位置和速度直到发现满足最大迭代次数的全局最优解。粒子i第k次迭代的速度和位置更新方程如下：

其中：c1、c2为学习因子；rand（）为［0，1］之间的随机数；w为惯性权重；Pid为粒子本身最优解，即局部最优解；Pgd为所有Pid中的最优值，即全局最优解。粒子群在开始迭代时的初始位置和速度是随机的，然后依照公式（3）、（4）迭代，直至满足约束函数。

由于实际问题中，中和轴的平移和偏转为优化问题的两个变量，此时粒子群算法的搜索空间为二维空间，可通过多目标粒子群优化算法（MOPSO）搜索中和轴的位置。

相对于单目标优化问题，多目标优化问题的关键在于如何选择个体最优和群体最优。

本文采用线性加权法将多目标函数转化为单目标函数，其核心思想是根据各个目标f（x）的重要程度，分别赋予一个非负的权系数，然后把这些带权的目标加起来构造评价函数通过这个评价函数，将多目标优化问题转化为单目标优化问题求解这个单目标问题可以得到最优解。

2.2 基于粒子群算法的中和轴确定及改进的Smith法

对于剖面中和轴的求解，问题的数学模型为：

变量—中和轴的垂向位置z和与水平轴的转角α；

约束函数—f1≤0.01，f2≤0.01。

粒子群搜索中和轴的具体流程如下：

（1）初始化粒子群：基于上一次曲率步得到的中和轴位置，在中和轴上下的最大可能移动范围内等距离划分得到初始的中和轴粒子群（粒子在整个搜索空间内均匀分布），存入初始集POP0中，粒子数为中和轴位移步数，n2为中和轴转角步数，本文的粒子数n=50×50=2 500，步长step（）z和）视剖面尺寸而定。初始化粒子的速度v（i）=0，i∈［1，…，n］，设置粒子的惯性权重w、学习因子c、迭代次数tmax、粒子最大速度vmax，惯性权重因子采用线性递减方式，其中，学习因子为迭代次数；限定粒子最大移动范围

（3）更新粒子群：设置迭代步数为100，第j步POPj第i个粒子的速度为，位置为，采用目标函数评价粒子，为第j步粒子选择个体最优解和群体最优解依据以下公式，更新中和轴位置，得到第j+1步粒子群：

（4）达到迭代步数时，如满足收敛要求，则结束搜索；如未满足收敛要求，则返回步骤（1）继续搜索直至满足收敛要求。

进一步，将基于PSO的中和轴确定方法与Smith法结合，建立改进的Smith法以实现非对称船体剖面的极限弯矩计算，其流程图如图3所示。

图3基于粒子群算法的Smith法的基本流程图Fig.3 Flow chart of the PSO-based Smith’s method

3 计算结果与分析

本文选取Dow1/3护卫舰试验模型[8]作为参考算例。该算例船在过去的几十年里一直是人们使用各种计算方法计算的模板，且已存在可参考的计算结果，因此可用来验证提出的PSO算法是否合理。

3.1 计算模型与工况定义

Dow1/3护卫舰的半中横剖面图如图4所示。船体剖面的加强筋类型及尺寸参数如表1所示，且船用钢材的杨氏模量和泊松比分别取206 GPa和0.3。

表1 Dow1/3护卫舰试验模型的横剖面型材表Tab.1 Dimensions of longitudinals of Dow’s test hull-1/3 scale frigate

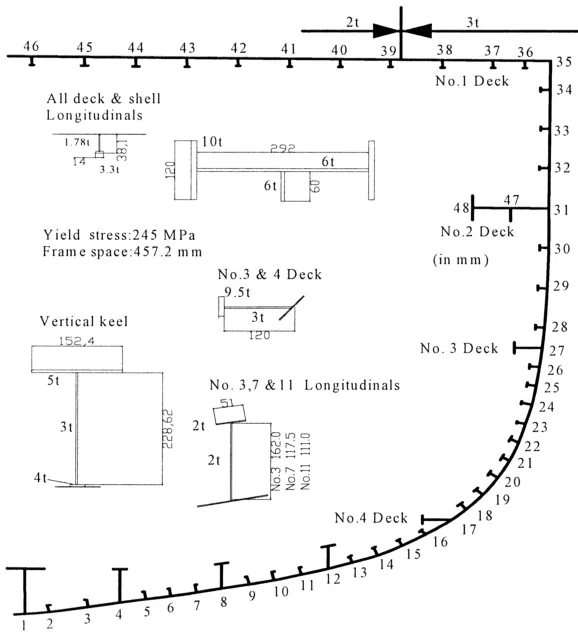
图4 Dow1/3护卫舰试验模型的半中横剖面图Fig.4 Half mid-ship section of Dow’s test hull-1/3 scale frigate

考虑船体结构和倾斜状态，选取了Dow试验模型完整正浮工况和多个破损横倾工况作为计算工况，具体情况如表2所示。其中，破损状态的破口位置位于右舷，破口中心坐标（y，z）为（2.0 m，2.8 m），破损半径为1.0 m。

3.2 权重系数分析

采用线性加权法解决多目标粒子群优化问题时，权重系数的选取是影响计算精度的一个重要方面。本文首先采用Case 2开展计算分析，对于权重系数w1、w2分别选取以下几组分配方式进行计算：（1）w1=0.2，w2=0.8；（2）w1=w2=0.5；（3）w1=0.8，w2=0.2。由于中垂及中拱状态下得到的收敛系数值变化趋势及数值基本一致，故只列出中垂状态下的力平衡误差值和力矢量平衡误差值，如图5所示。

表2计算工况定义Tab.2 Difinition of calculation condition

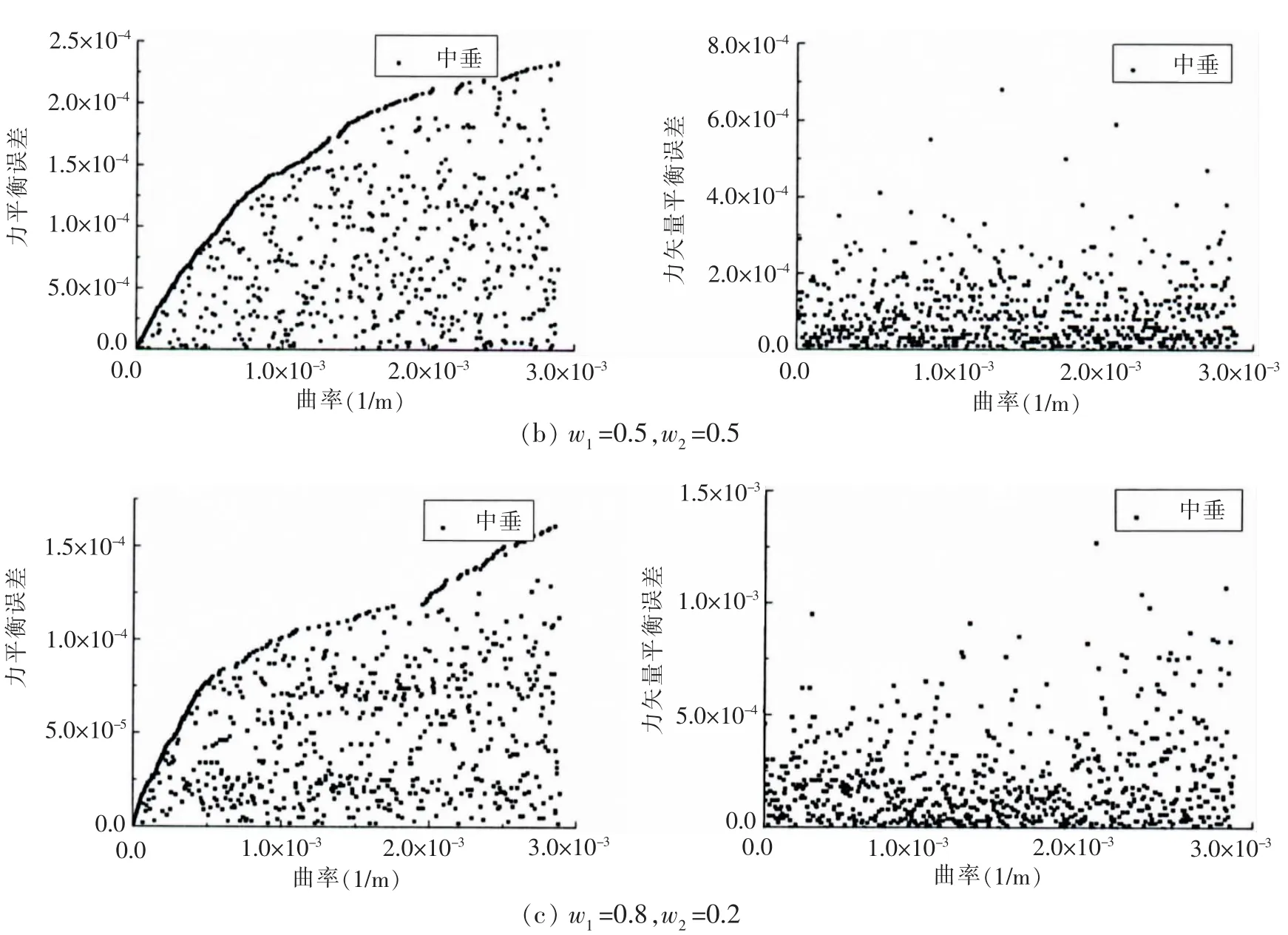
图5不同权重分配下Dow1/3护卫舰破损船中垂工况下的力平衡误差和力矢量平衡误差Fig.5 Force equilibrium errors and force vector equilibrium errors in the calculation with different weight coefficients for the damaged hull in sagging condition

通过计算发现，随着船体梁曲率的增加，不同权重比重下的力平衡误差值和力矢量平衡误差值均达到了收敛要求，且远小于收敛系数。此外，不同权重系数的分配下，得到的力平衡误差或力矢量平衡误差值相差不大。这说明权重系数的分配对收敛模式没有明显的影响，故后续的计算采用w1=w2=0.5的权重分配。

3.3 不同工况计算结果与分析

（1）完整工况Case1计算结果

分别采用基于PSO的改进Smith法和基于线性搜索法的改进Smith法对Dow1/3护卫舰试验模型完整工况Case1进行计算，得到的中垂、中拱状态下剖面中和轴移动情况及极限弯矩结果如图6所示，将中垂、中拱状态下剖面极限弯矩结果列入表3，并与现有的文献中所有极限强度计算方法得到的值进行对比，其中Ms为中垂弯矩，Mh为中拱弯矩。

图6 Dow1/3护卫舰完整船正浮状态下中和轴的移动及弯矩结果Fig.6 Bending moment&motions of NA-curvature relationships of the Dow’s 1/3 frigate model in intact condition

由图6可得：采用基于PSO的改进Smith法计算极限弯矩时，随着船体梁曲率的增加，剖面中和轴的移动曲线及船体剖面弯矩-曲率曲线均与基于线性搜索法的改进Smith法计算结果有很好的吻合性，这表明PSO应用于Smith法中和轴的计算可行，能够很好地实现算法目的。

通过与表3列出的结果对比发现，基于PSO的改进Smith法计算结果与其他学者计算结果吻合良好。中垂情况下，与实验值相比误差值为2.8%；中拱情况下，参照Paik采用非线性有限元计算方法的结果，结果相比误差为6.64%。另外，基于PSO的Smith法与基于线性搜索法的改进Smith法对于完整船对称剖面得到的计算结果完全吻合，表明基于PSO算法的Smith方法在实际计算中的可行性。

表3 Dow1/3护卫舰试验模型完整船的所有极限强度计算结果Tab.3 Summary of ultimate strength of Dow’s test hull-1/3 scale frigate

（2）破损工况计算结果

采用基于PSO的改进Smith法对Dow1/3护卫舰试验模型Case 2-4工况计算剖面极限弯矩，与基于线性搜索法的改进Smith法进行结果对比，得到的中垂、中拱状态下剖面中和轴移动情况以及极限弯矩对比图如图7-9所示。

图7 Dow1/3护卫舰破损船左倾10°状态下中和轴的移动及弯矩结果Fig.7 Bending moment&motions of NA-curvature relationships of the Dow’s 1/3 frigate model with damaged hull and a heeling angle of 10°

图8 Dow1/3护卫舰破损船左倾20°状态下中和轴的移动及弯矩结果Fig.8 Bending moment&motions of NA-curvature relationships of the Dow’s 1/3 frigate model with damaged hull and a heeling angle of 20°

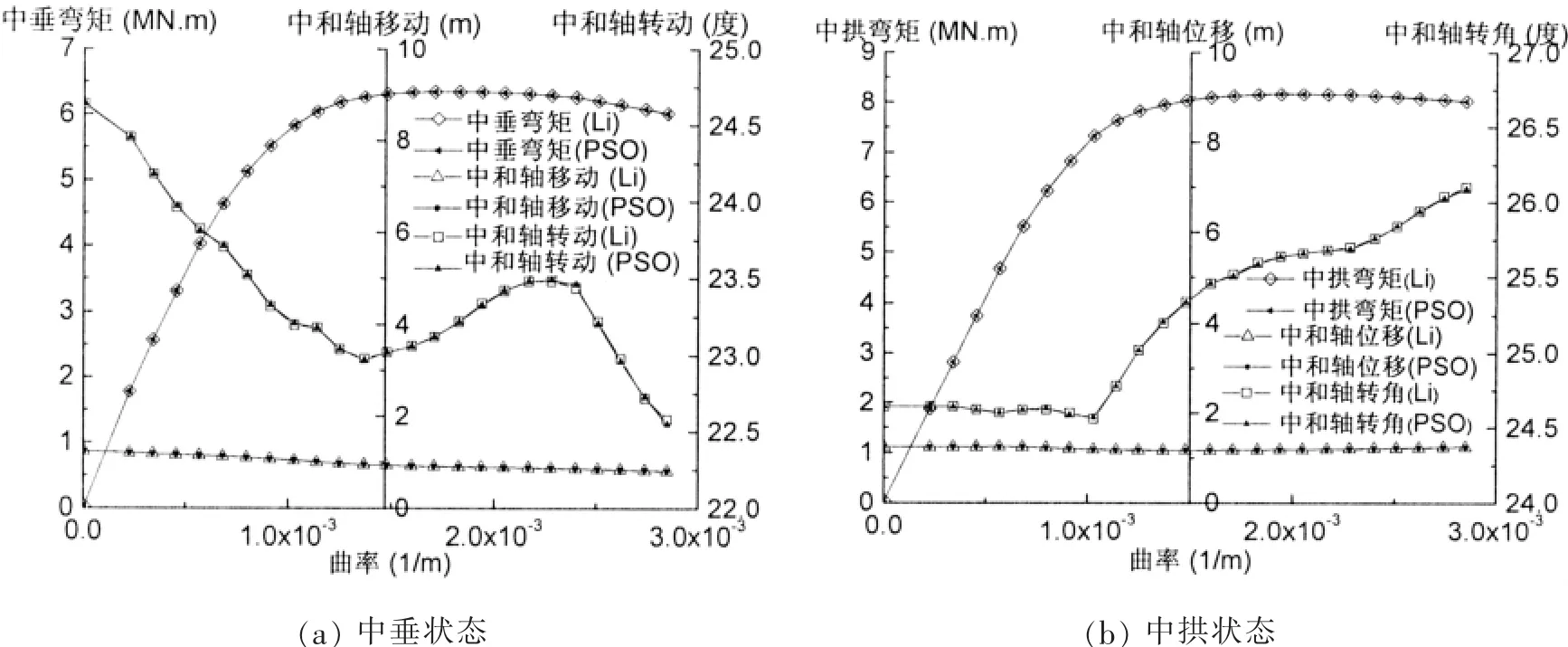
图9 Dow1/3护卫舰破损船左倾30°状态下中和轴的移动及弯矩结果Fig.9 Bending moment&motions of NA-curvature relationships of the Dow’s 1/3 frigate model with damaged hull and a heeling angle of 30°

从图7-9可以看出，对于Dow1/3护卫舰试验模型，其计算得到的中和轴移动、船体剖面弯矩均与李陈峰等提出的改进Smith算法计算结果基本吻合，中和轴移动趋势及弯矩变化趋势基本一致。这说明，本文提出的基于PSO算法的Smith方法用于极限强度计算是可行的，且精度较高。